Difference between revisions of "Polynomial of best approximation"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | p0737301.png | ||
| + | $#A+1 = 50 n = 1 | ||
| + | $#C+1 = 50 : ~/encyclopedia/old_files/data/P073/P.0703730 Polynomial of best approximation | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A polynomial furnishing the best approximation of a function $ x ( t) $ | |
| + | in some metric, relative to all polynomials constructed from a given (finite) system of functions. If $ X $ | ||
| + | is a normed linear function space (such as $ C [ a, b] $ | ||
| + | or $ L _ {p} ( a, b) $, | ||
| + | $ p \geq 1 $), | ||
| + | and if | ||
| − | + | $$ | |
| + | U _ {n} = \{ u _ {1} ( t) \dots u _ {n} ( t) \} | ||
| + | $$ | ||
| + | |||
| + | is a system of linearly independent functions in $ X $, | ||
| + | then for any $ x \in X $ | ||
| + | the (generalized) polynomial of best approximation | ||
| + | |||
| + | $$ \tag{* } | ||
| + | \widetilde{u} ( t) = \widetilde{u} ( x, t) = \ | ||
| + | \sum _ {k = 1 } ^ { n } \widetilde{c} _ {k} u _ {k} ( t), | ||
| + | $$ | ||
defined by the relation | defined by the relation | ||
| − | + | $$ | |
| + | \| x - \widetilde{u} \| = \ | ||
| + | \min _ {\{ c _ {k} \} } \left \| x - | ||
| + | \sum _ {k = 1 } ^ { n } c _ {k} u _ {k} \right \| , | ||
| + | $$ | ||
| − | exists. The polynomial of best approximation is unique for all | + | exists. The polynomial of best approximation is unique for all $ x \in X $ |
| + | if $ X $ | ||
| + | is a space with a strictly convex norm (i.e. if $ \| x \| = \| y \| $ | ||
| + | and $ x \neq y $, | ||
| + | then $ \| x + y \| < \| x \| + \| y \| $). | ||
| + | This is the case for $ L _ {p} ( a, b) $, | ||
| + | $ 1 < p < \infty $. | ||
| + | In $ C [ a, b] $, | ||
| + | which has a norm that is not strictly convex, the polynomial of best approximation for any $ x \in C [ a, b] $ | ||
| + | is unique if $ U _ {n} $ | ||
| + | is a [[Chebyshev system|Chebyshev system]] on $ [ a, b] $, | ||
| + | i.e. if each polynomial | ||
| − | + | $$ | |
| + | u ( t) = \sum _ {k = 1 } ^ { n } c _ {k} u _ {k} ( t) \neq 0 | ||
| + | $$ | ||
| − | has at most | + | has at most $ n - 1 $ |
| + | zeros on $ [ a, b] $. | ||
| + | In particular, one has uniqueness in the case of the (usual) algebraic polynomials in $ C [ a, b] $, | ||
| + | and also for the trigonometric polynomials in the space $ C _ {2 \pi } $ | ||
| + | of continuous $ 2 \pi $- | ||
| + | periodic functions on the real line, with the uniform metric. If the polynomial of best approximation exists and is unique for any $ x \in X $, | ||
| + | it is a continuous function of $ x $. | ||
| − | Necessary and sufficient conditions for a polynomial to be a best approximation in the spaces | + | Necessary and sufficient conditions for a polynomial to be a best approximation in the spaces $ C[ a, b] $ |
| + | and $ L _ {p} [ a, b] $ | ||
| + | are known. For example, one has Chebyshev's theorem: If $ U _ {n} $ | ||
| + | is a Chebyshev system, then the polynomial (*) is a polynomial of best approximation for a function $ x \in C [ a, b] $ | ||
| + | in the metric of $ C [ a, b] $ | ||
| + | if and only if there exists a system of $ n + 1 $ | ||
| + | points $ t _ {i} $, | ||
| + | $ a \leq t _ {1} < {} \dots < t _ {n + 1 } \leq b $, | ||
| + | at which the difference | ||
| − | + | $$ | |
| + | \Delta ( t) = x ( t) - \widetilde{u} ( t) | ||
| + | $$ | ||
assumes values | assumes values | ||
| − | + | $$ | |
| + | \pm \max _ {a \leq t \leq b } | \Delta ( t) | | ||
| + | $$ | ||
and, moreover, | and, moreover, | ||
| − | + | $$ | |
| + | \Delta ( t _ {i + 1 } ) = - \Delta ( t _ {i} ),\ \ | ||
| + | i = 1 \dots n. | ||
| + | $$ | ||
| − | The polynomial (*) is a polynomial of best approximation for a function | + | The polynomial (*) is a polynomial of best approximation for a function $ x ( t) \in L _ {p} [ a, b] $, |
| + | $ p > 1 $, | ||
| + | in the metric of that space, if and only if for $ k = 1 \dots n $, | ||
| − | + | $$ | |
| + | \int\limits _ { a } ^ { b } | ||
| + | u _ {k} ( t) | x ( t) - \widetilde{u} ( t) | ^ {p - 1 } \ | ||
| + | \mathop{\rm sign} [ x ( t) - \widetilde{u} ( t)] dt = 0. | ||
| + | $$ | ||
| − | In | + | In $ L _ {1} [ a, b] $, |
| + | the conditions | ||
| − | + | $$ | |
| + | \int\limits _ { a } ^ { b } | ||
| + | u _ {k} ( t) \mathop{\rm sign} [ x ( t) - \widetilde{u} ( t)] dt = 0,\ \ | ||
| + | k = 1 \dots n, | ||
| + | $$ | ||
| − | are sufficient for | + | are sufficient for $ \widetilde{u} ( t) $ |
| + | to be a polynomial of best approximation for $ x \in L _ {1} [ a, b] $, | ||
| + | and if the measure of the set of all points $ t \in ( a, b) $ | ||
| + | at which $ x ( t) = \widetilde{u} ( t) $ | ||
| + | is zero, they are also necessary; see also [[Markov criterion|Markov criterion]]. | ||
There exist algorithms for the approximate construction of polynomials of best uniform approximation (see e.g. [[#References|[3]]], [[#References|[5]]]). | There exist algorithms for the approximate construction of polynomials of best uniform approximation (see e.g. [[#References|[3]]], [[#References|[5]]]). | ||
| Line 43: | Line 120: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> N.I. [N.I. Akhiezer] Achiezer, "Theory of approximation" , F. Ungar (1956) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> N.P. Korneichuk, "Extremal problems in approximation theory" , Moscow (1976) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> V.K. Dzyadyk, "Introduction to the theory of uniform approximation of functions by polynomials" , Moscow (1977) (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.M. Tikhomirov, "Some problems in approximation theory" , Moscow (1976) (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> P.J. Laurent, "Approximation et optimisation" , Hermann (1972)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> E.Ya. Remez, "Foundations of numerical methods of Chebyshev approximation" , Kiev (1969) (In Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N.I. [N.I. Akhiezer] Achiezer, "Theory of approximation" , F. Ungar (1956) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> N.P. Korneichuk, "Extremal problems in approximation theory" , Moscow (1976) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> V.K. Dzyadyk, "Introduction to the theory of uniform approximation of functions by polynomials" , Moscow (1977) (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.M. Tikhomirov, "Some problems in approximation theory" , Moscow (1976) (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> P.J. Laurent, "Approximation et optimisation" , Hermann (1972)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> E.Ya. Remez, "Foundations of numerical methods of Chebyshev approximation" , Kiev (1969) (In Russian)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A.M. Pinkus, "On <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073730/p07373051.png" />-approximation" , Cambridge Univ. Press (1989)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Schönhage, "Approximationstheorie" , de Gruyter (1971)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> G.A. Watson, "Approximation theory and numerical methods" , Wiley (1980)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> E.W. Cheney, "Introduction to approximation theory" , McGraw-Hill (1966) pp. Chapts. 4&6</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> M.J.D. Powell, "Approximation theory and methods" , Cambridge Univ. Press (1981)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> J.R. Rice, "The approximation of functions" , '''1. Linear theory''' , Addison-Wesley (1964)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> T.J. Rivlin, "An introduction to the approximation of functions" , Blaisdell (1969)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A.M. Pinkus, "On <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073730/p07373051.png" />-approximation" , Cambridge Univ. Press (1989)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Schönhage, "Approximationstheorie" , de Gruyter (1971)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> G.A. Watson, "Approximation theory and numerical methods" , Wiley (1980)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> E.W. Cheney, "Introduction to approximation theory" , McGraw-Hill (1966) pp. Chapts. 4&6</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> M.J.D. Powell, "Approximation theory and methods" , Cambridge Univ. Press (1981)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> J.R. Rice, "The approximation of functions" , '''1. Linear theory''' , Addison-Wesley (1964)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> T.J. Rivlin, "An introduction to the approximation of functions" , Blaisdell (1969)</TD></TR></table> | ||
Latest revision as of 08:06, 6 June 2020
A polynomial furnishing the best approximation of a function $ x ( t) $
in some metric, relative to all polynomials constructed from a given (finite) system of functions. If $ X $
is a normed linear function space (such as $ C [ a, b] $
or $ L _ {p} ( a, b) $,
$ p \geq 1 $),
and if
$$ U _ {n} = \{ u _ {1} ( t) \dots u _ {n} ( t) \} $$
is a system of linearly independent functions in $ X $, then for any $ x \in X $ the (generalized) polynomial of best approximation
$$ \tag{* } \widetilde{u} ( t) = \widetilde{u} ( x, t) = \ \sum _ {k = 1 } ^ { n } \widetilde{c} _ {k} u _ {k} ( t), $$
defined by the relation
$$ \| x - \widetilde{u} \| = \ \min _ {\{ c _ {k} \} } \left \| x - \sum _ {k = 1 } ^ { n } c _ {k} u _ {k} \right \| , $$
exists. The polynomial of best approximation is unique for all $ x \in X $ if $ X $ is a space with a strictly convex norm (i.e. if $ \| x \| = \| y \| $ and $ x \neq y $, then $ \| x + y \| < \| x \| + \| y \| $). This is the case for $ L _ {p} ( a, b) $, $ 1 < p < \infty $. In $ C [ a, b] $, which has a norm that is not strictly convex, the polynomial of best approximation for any $ x \in C [ a, b] $ is unique if $ U _ {n} $ is a Chebyshev system on $ [ a, b] $, i.e. if each polynomial
$$ u ( t) = \sum _ {k = 1 } ^ { n } c _ {k} u _ {k} ( t) \neq 0 $$
has at most $ n - 1 $ zeros on $ [ a, b] $. In particular, one has uniqueness in the case of the (usual) algebraic polynomials in $ C [ a, b] $, and also for the trigonometric polynomials in the space $ C _ {2 \pi } $ of continuous $ 2 \pi $- periodic functions on the real line, with the uniform metric. If the polynomial of best approximation exists and is unique for any $ x \in X $, it is a continuous function of $ x $.
Necessary and sufficient conditions for a polynomial to be a best approximation in the spaces $ C[ a, b] $ and $ L _ {p} [ a, b] $ are known. For example, one has Chebyshev's theorem: If $ U _ {n} $ is a Chebyshev system, then the polynomial (*) is a polynomial of best approximation for a function $ x \in C [ a, b] $ in the metric of $ C [ a, b] $ if and only if there exists a system of $ n + 1 $ points $ t _ {i} $, $ a \leq t _ {1} < {} \dots < t _ {n + 1 } \leq b $, at which the difference
$$ \Delta ( t) = x ( t) - \widetilde{u} ( t) $$
assumes values
$$ \pm \max _ {a \leq t \leq b } | \Delta ( t) | $$
and, moreover,
$$ \Delta ( t _ {i + 1 } ) = - \Delta ( t _ {i} ),\ \ i = 1 \dots n. $$
The polynomial (*) is a polynomial of best approximation for a function $ x ( t) \in L _ {p} [ a, b] $, $ p > 1 $, in the metric of that space, if and only if for $ k = 1 \dots n $,
$$ \int\limits _ { a } ^ { b } u _ {k} ( t) | x ( t) - \widetilde{u} ( t) | ^ {p - 1 } \ \mathop{\rm sign} [ x ( t) - \widetilde{u} ( t)] dt = 0. $$
In $ L _ {1} [ a, b] $, the conditions
$$ \int\limits _ { a } ^ { b } u _ {k} ( t) \mathop{\rm sign} [ x ( t) - \widetilde{u} ( t)] dt = 0,\ \ k = 1 \dots n, $$
are sufficient for $ \widetilde{u} ( t) $ to be a polynomial of best approximation for $ x \in L _ {1} [ a, b] $, and if the measure of the set of all points $ t \in ( a, b) $ at which $ x ( t) = \widetilde{u} ( t) $ is zero, they are also necessary; see also Markov criterion.
There exist algorithms for the approximate construction of polynomials of best uniform approximation (see e.g. [3], [5]).
References
| [1] | N.I. [N.I. Akhiezer] Achiezer, "Theory of approximation" , F. Ungar (1956) (Translated from Russian) |
| [2] | N.P. Korneichuk, "Extremal problems in approximation theory" , Moscow (1976) (In Russian) |
| [3] | V.K. Dzyadyk, "Introduction to the theory of uniform approximation of functions by polynomials" , Moscow (1977) (In Russian) |
| [4] | V.M. Tikhomirov, "Some problems in approximation theory" , Moscow (1976) (In Russian) |
| [5] | P.J. Laurent, "Approximation et optimisation" , Hermann (1972) |
| [6] | E.Ya. Remez, "Foundations of numerical methods of Chebyshev approximation" , Kiev (1969) (In Russian) |
Comments
References
| [a1] | A.M. Pinkus, "On 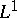 -approximation" , Cambridge Univ. Press (1989) -approximation" , Cambridge Univ. Press (1989) |
| [a2] | A. Schönhage, "Approximationstheorie" , de Gruyter (1971) |
| [a3] | G.A. Watson, "Approximation theory and numerical methods" , Wiley (1980) |
| [a4] | E.W. Cheney, "Introduction to approximation theory" , McGraw-Hill (1966) pp. Chapts. 4&6 |
| [a5] | M.J.D. Powell, "Approximation theory and methods" , Cambridge Univ. Press (1981) |
| [a6] | J.R. Rice, "The approximation of functions" , 1. Linear theory , Addison-Wesley (1964) |
| [a7] | T.J. Rivlin, "An introduction to the approximation of functions" , Blaisdell (1969) |
Polynomial of best approximation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Polynomial_of_best_approximation&oldid=18661