Difference between revisions of "Polynomial convexity"
(Importing text file) |
m (Automatically changed introduction) |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 213 formulas, 204 were replaced by TEX code.--> | |
| − | is called the polynomially convex hull of | + | {{TEX|semi-auto}}{{TEX|part}} |
| + | Let $\mathcal{P}$ denote the set of holomorphic polynomials on $\mathbf{C} ^ { n }$ (cf. also [[Analytic function|Analytic function]]). Let $K$ be a compact set in $\mathbf{C} ^ { n }$ and let $\| P \| _ { K } = \operatorname { max } _ { z \in K } | P ( z ) |$ be the sup-norm of $P \in \mathcal{P}$ on $K$. The set | ||
| + | |||
| + | \begin{equation*} \hat { K } = \{ z \in {\bf C} ^ { n } : | P ( z ) | \leq \| P \| _ { K } , \forall P \in {\cal P} \}, \end{equation*} | ||
| + | |||
| + | is called the polynomially convex hull of $K$. If $\hat { K } = K$ one says that $K$ is polynomially convex. | ||
An up-to-date (as of 1998) text dealing with polynomial convexity is [[#References|[a3]]], while [[#References|[a13]]] and [[#References|[a27]]] contain some sections on polynomial convexity, background and older results. The paper [[#References|[a24]]] is an early study on polynomial convexity. | An up-to-date (as of 1998) text dealing with polynomial convexity is [[#References|[a3]]], while [[#References|[a13]]] and [[#References|[a27]]] contain some sections on polynomial convexity, background and older results. The paper [[#References|[a24]]] is an early study on polynomial convexity. | ||
| − | Polynomial convexity arises naturally in the context of function algebras (cf. also [[Algebra of functions|Algebra of functions]]): Let | + | Polynomial convexity arises naturally in the context of function algebras (cf. also [[Algebra of functions|Algebra of functions]]): Let $P ( K )$ denote the [[Uniform algebra|uniform algebra]] generated by the holomorphic polynomials on $K$ with the sup-norm. The maximal ideal space $M$ of $P ( K )$ is the set of homomorphisms mapping $P ( K )$ onto $\mathbf{C}$, endowed with the topology inherited from the dual space $P ( K ) ^ { * }$. It can be identified with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130100/p13010019.png"/> via |
| − | + | \begin{equation*} z \in \widehat { K } \leftrightarrow m _ { z }, \end{equation*} | |
| − | + | \begin{equation*} P \mapsto P ( z ) , P \in \mathcal{P}. \end{equation*} | |
| − | Moreover, if | + | Moreover, if $A$ is any finitely generated function algebra on a compact Hausdorff space, then $A$ is isomorphic to $P ( K )$, where for $K$ one can take the joint spectrum of the generators of $A$ (cf. also [[Spectrum of an operator|Spectrum of an operator]]). |
| − | By the Riesz representation theorem (cf. [[Riesz theorem(2)|Riesz theorem]]) there exists for every | + | By the Riesz representation theorem (cf. [[Riesz theorem(2)|Riesz theorem]]) there exists for every $z \in \hat { K }$ at least one representing measure $\mu _ { z }$, that is, a [[Probability measure|probability measure]] $\mu _ { z }$ on $K$ such that |
| − | + | \begin{equation*} P ( z ) = m _ { z } ( P ) = \int _ { K } P ( \zeta ) d \mu _ { z } ( \zeta ) , P \in \mathcal{P}. \end{equation*} | |
| − | One calls | + | One calls $\mu _ { z }$ a Jensen measure if it has the stronger property |
| − | + | \begin{equation*} \operatorname { log } | P ( z ) | \leq \int _ { K } \operatorname { log } | P ( \zeta ) | d \mu _ { z } ( \zeta ) , P \in \mathcal{P}. \end{equation*} | |
| − | It can be shown that for each | + | It can be shown that for each $z \in \hat { K }$ there exists a Jensen measure $\mu _ { z }$. See e.g. [[#References|[a27]]]. |
| − | For compact sets | + | For compact sets $K$ in $\mathbf{C}$ one obtains <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130100/p13010038.png"/> by "filling in the holes" of $K$, that is, $\hat { K } = \mathbf{C} \backslash \Omega _ { \infty }$, where $\Omega _ { \infty }$ is the unbounded component of $\mathbf{C} \backslash K$. In $\mathbf{C} ^ { n }$, $n > 1$, there is no such a simple topological description. |
Early results on polynomial convexity, cf. [[#References|[a13]]], are | Early results on polynomial convexity, cf. [[#References|[a13]]], are | ||
| − | Oka's theorem: If | + | Oka's theorem: If $K$ is a polynomially convex set in $\mathbf{C} ^ { n }$ and $f$ is holomorphic on a neighbourhood of $K$, then $f$ can be written on $K$ as a uniform limit of polynomials. Cf. also [[Oka theorems|Oka theorems]]. |
| − | Browder's theorem: If | + | Browder's theorem: If $K$ is polynomially convex in $\mathbf{C} ^ { n }$, then $H ^ { p } ( K , {\bf C} ) = 0$ for $p \geq n$. |
| − | Here, | + | Here, $H ^ { p } ( K , \mathbf{C} )$ is the $p$th [[Čech cohomology|Čech cohomology]] group. More recently (1994), the following topological result was obtained, cf. [[#References|[a9]]], [[#References|[a3]]]: |
| − | Forstnerič' theorem: Let | + | Forstnerič' theorem: Let $K$ be a polynomially convex set in $\mathbf{C} ^ { n }$, $n \geq 2$. Then |
| − | + | \begin{equation*} H _ { k } ( \mathbf{C} ^ { n } \backslash K ; G ) = 0,1 \leq k \leq n - 1, \end{equation*} | |
and | and | ||
| − | + | \begin{equation*} \pi _ { k } ( \mathbf{C} ^ { n } \backslash K ) = 0,1 \leq k \leq n - 1. \end{equation*} | |
| − | Here, | + | Here, $H _ { k } ( X , G )$ denotes the $k$th [[Homology group|homology group]] of $X$ with coefficients in an Abelian group $G$ and $\pi _ { k } ( X )$ is the $k$th homotopy group of $X$. |
| − | One method to find <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130100/p13010069.png" /> is by means of analytic discs. Let | + | One method to find <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130100/p13010069.png"/> is by means of analytic discs. Let $\Delta$ be the unit disc in $\mathbf{C}$ and let $T$ be its boundary. An analytic disc is (the image of) a holomorphic mapping $f : \Delta \rightarrow {\bf C} ^ { n }$ such that $f$ is continuous up to $T$. Similarly one defines an $H ^ { \infty }$-disc as a bounded holomorphic mapping $f : \Delta \rightarrow {\bf C} ^ { n }$. Its components are elements of the usual Hardy space $H ^ { \infty } ( \Delta )$ (cf. [[Hardy spaces|Hardy spaces]]). |
| − | Now, let | + | Now, let $K$ be compact in $\mathbf{C} ^ { n }$ and suppose that $f ( T ) \subset K$ for some analytic disc $f$. Then $f ( \Delta ) \subset \hat { K }$ by the [[Maximum principle|maximum principle]] applied to $P \circ f$ for polynomials $P \in \mathcal{P}$. The same goes for $H ^ { \infty }$-discs whose boundary values are almost everywhere in $K$. One says that the disc $f$ is glued to $K$. Next, one says that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130100/p13010091.png"/> has analytic structure at $p \in \hat{K}$ if there exists a non-constant analytic disc $f$ such that $f ( 0 ) = p$ and the image of $f$ is contained in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130100/p13010096.png"/>. |
| − | It was a major question whether | + | It was a major question whether $\hat{K} \backslash K$ always has analytic structure. Moreover, when is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130100/p13010098.png"/> obtained by glueing discs to $K$? One positive result in this direction is due to H. Alexander [[#References|[a1]]]; a corollary of his work is as follows: If $K$ is a rectifiable curve in $\mathbf{C} ^ { n }$, then either $\hat { K } = K$ and $P ( K ) = C ( K )$, or $\hat{K} \backslash K$ is a pure $1$-dimensional analytic subset of $\mathbf{C} ^ { n } \backslash K$ (cf. also [[Analytic set|Analytic set]]). If $K$ is a rectifiable arc, $K$ is polynomially convex and $P ( K ) = C ( K )$. |
| − | See [[#References|[a1]]] for the complete formulation. Alexander's result is an extension of pioneering work of J. Wermer, cf. [[#References|[a30]]], E. Bishop and, later, G. Stolzenberg [[#References|[a26]]], who dealt with real-analytic, respectively | + | See [[#References|[a1]]] for the complete formulation. Alexander's result is an extension of pioneering work of J. Wermer, cf. [[#References|[a30]]], E. Bishop and, later, G. Stolzenberg [[#References|[a26]]], who dealt with real-analytic, respectively $C ^ { 1 }$, curves. Wermer [[#References|[a29]]] gave the first example of an arc in $\mathbf{C} ^ { 3 }$ that is not polynomially convex, cf. [[#References|[a3]]]. However, Gel'fand's problem (i.e., let $\gamma$ be an arc in $\mathbf{C} ^ { n }$ such that $\hat{\gamma} = \gamma$; is it true that $P ( \gamma ) = C ( \gamma )$?) is still open (2000). Under the additional assumption that its projections into the complex coordinate planes have $2$-dimensional [[Hausdorff measure|Hausdorff measure]] $0$, the answer is positive, see [[#References|[a3]]]. |
| − | F.R. Harvey and H.B. Lawson gave a generalization to higher-dimensional | + | F.R. Harvey and H.B. Lawson gave a generalization to higher-dimensional $K$, cf. [[#References|[a12]]], which includes the following. |
| − | Let | + | Let $p \geq 1$. If $K$ is a $C ^ { 2 }$ $( 2 p + 1 )$-dimensional submanifold of $\mathbf{C} ^ { n }$ and at each point of $K$ the tangent space to $K$ contains a $p$-dimensional complex subspace, then $K$ is the boundary of an analytic variety (in the sense of Stokes' theorem). |
| − | Another positive result is contained in the work of E. Bedford and W. Klingenberg, cf. [[#References|[a4]]]: Suppose | + | Another positive result is contained in the work of E. Bedford and W. Klingenberg, cf. [[#References|[a4]]]: Suppose $\Gamma \subset {\bf C} ^ { 2 }$ is the graph of a $C ^ { 2 }$-function $\phi$ over the boundary of a strictly convex domain $\Omega \subset \mathbf{C} \times \mathbf{R}$. Then $\widehat{\Gamma}$ is the graph of a Lipschitz-continuous extension $\Phi$ of $\phi$ on $\Omega$. Moreover, $\widehat{\Gamma}$ is foliated with analytic discs (cf. also [[Foliation|Foliation]]). |
The work of Bedford and Klingenberg has been generalized in various directions in [[#References|[a16]]], [[#References|[a21]]] and [[#References|[a7]]]. One ingredient of this theorem is work of Bishop [[#References|[a5]]], which gives conditions that guarantee locally the existence of analytic discs with boundary in real submanifolds of sufficiently high dimension. See [[#References|[a11]]], [[#References|[a32]]] and [[#References|[a15]]] for results along this line. | The work of Bedford and Klingenberg has been generalized in various directions in [[#References|[a16]]], [[#References|[a21]]] and [[#References|[a7]]]. One ingredient of this theorem is work of Bishop [[#References|[a5]]], which gives conditions that guarantee locally the existence of analytic discs with boundary in real submanifolds of sufficiently high dimension. See [[#References|[a11]]], [[#References|[a32]]] and [[#References|[a15]]] for results along this line. | ||
| − | A third situation that is fairly well understood is when | + | A third situation that is fairly well understood is when $K \subset \mathbf{C} ^ { n + 1 }$ is a compact set fibred over $T$, that is, $K$ is of the form $K = \{ ( z , w ) : z \in T , w \in K _ { z } \}$, where $K _ { z }$ is a compact set in $\mathbf{C} ^ { n }$ depending on $z$. |
| − | In this case the following is true: Let | + | In this case the following is true: Let $K \subset \mathbf{C} ^ { 2 }$ be a compact fibration over the circle $T$ and suppose that for each $z$ the fibre $K _ { z }$ is connected and simply connected. Then $\hat{K} \backslash K$ is the union of graphs $\Gamma _ { f }$, where $f \in H ^ { \infty } ( \Delta )$ and the boundary values $f ^ { * } ( z )$ are in $K _ { z }$ for almost all $z \in T$. |
| − | Of course, it is possible that | + | Of course, it is possible that $\hat{K} \backslash K$ is empty. The present theorem is due to Z. Slodkowski, [[#References|[a22]]], earlier results are in [[#References|[a2]]] and [[#References|[a10]]]. Slodkowski proved a similar theorem in $\mathbf{C} ^ { n + 1}$ under the assumption that the fibres are convex, see [[#References|[a23]]]. |
| − | Despite these positive results, in general | + | Despite these positive results, in general $\hat{K} \backslash K$ need not have analytic structure. This has become clear from examples by Stolzenberg [[#References|[a25]]] and Wermer [[#References|[a31]]]. Presently (2000) it is not known whether <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130100/p130100157.png"/> has analytic structure everywhere if $K$ is a (real) submanifold of $\mathbf{C} ^ { n }$, nor is it known under what conditions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130100/p130100160.png"/> is obtained by glueing discs to $K$. |
| − | However, it has been shown that in a weaker sense there is always a kind of analytic structure in polynomial hulls. Let | + | However, it has been shown that in a weaker sense there is always a kind of analytic structure in polynomial hulls. Let $d \theta$ denote [[Lebesgue measure|Lebesgue measure]] on the circle $T$ and let $f ^ { * } d \theta$ denote the push-forward of $d \theta$ under a continuous mapping $f : T \rightarrow \mathbf{C} ^ { n }$. Let also $K$ be a compact set in $\mathbf{C} ^ { n }$. The following are equivalent: |
| − | 1) | + | 1) $z \in \hat { K }$ and $\mu _ { z }$ is a Jensen measure for $z$ supported on $K$; |
| − | 2) There exists a sequence of analytic discs | + | 2) There exists a sequence of analytic discs $f _ { j } : \Delta \rightarrow \mathbf{C} ^ { n }$ such that $f _ { j } ( 0 ) \rightarrow z$ and $f _ { j } ^ { * } d \theta / 2 \pi \rightarrow \mu _ { z }$ in the weak-$*$ sense (cf. also [[Weak topology|Weak topology]]). |
| − | This was proved in [[#References|[a6]]]; [[#References|[a8]]] and [[#References|[a20]]] contain more information about additional nice properties that can be required from the sequence of analytic discs. Under suitable regularity conditions on | + | This was proved in [[#References|[a6]]]; [[#References|[a8]]] and [[#References|[a20]]] contain more information about additional nice properties that can be required from the sequence of analytic discs. Under suitable regularity conditions on $K$, it is shown in [[#References|[a19]]] that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130100/p130100178.png"/> consists of analytic discs $f$ such that $f ^ { - 1 } ( K ) \cap T$ has Lebesgue measure arbitrary close to $2 \pi$. |
| − | Another problem is to describe | + | Another problem is to describe $P ( K )$ assuming that $K = \hat { K }$ and given reasonable additional conditions on $K$. In particular, when can one conclude that $P ( K ) = C ( K )$? Recall that a real submanifold $M$ of $\mathbf{C} ^ { n }$ is totally real at $p \in M$ if the tangent space in $p$ does not contain a complex line (cf. also [[CR-submanifold|CR-submanifold]]). The Hörmander–Wermer theorem is as follows, cf. [[#References|[a14]]]: Let $M$ be a sufficiently smooth real submanifold of $\mathbf{C} ^ { n }$ and let $K _ { 0 }$ be the subset of $M$ consisting of points that are not totally real. If $K \subset M$ is a compact polynomially convex set that contains an $M$-neighbourhood of $K _ { 0 }$, then $P ( K )$ contains all continuous functions on $K$ that are on $K _ { 0 }$ the uniform limit of functions holomorphic in a neighbourhood of $K _ { 0 }$. |
| − | See [[#References|[a17]]] for a variation on this theme. One can deal with some situations where the manifold is replaced by a union of manifolds; e.g., B.M. Weinstock [[#References|[a28]]] gives necessary and sufficient conditions for any compact subset of the union of two totally real | + | See [[#References|[a17]]] for a variation on this theme. One can deal with some situations where the manifold is replaced by a union of manifolds; e.g., B.M. Weinstock [[#References|[a28]]] gives necessary and sufficient conditions for any compact subset of the union of two totally real $n$-dimensional subspaces of $\mathbf{C} ^ { n }$ to be polynomially convex; then also $P ( K ) = C ( K )$. See also [[#References|[a18]]]. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> H. Alexander, "Polynomial approximation and hulls in sets of finite linear measure in $\mathbf{C} ^ { n }$" ''Amer J. Math.'' , '''62''' (1971) pp. 65–74 {{MR|0284617}} {{ZBL|0221.32011}} </td></tr><tr><td valign="top">[a2]</td> <td valign="top"> H. Alexander, J. Wermer, "Polynomial hulls with convex fibres" ''Math. Ann.'' , '''281''' (1988) pp. 13–22</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> H. Alexander, J. Wermer, "Several complex variables and Banach algebras" , Springer (1998) {{MR|1482798}} {{ZBL|0894.46037}} </td></tr><tr><td valign="top">[a4]</td> <td valign="top"> E. Bedford, W. Klingenberg Jr., "On the envelope of holomorphy of a $2$-sphere in $\mathbf{C} ^ { 2 }$" ''J. Amer. Math. Soc.'' , '''4''' (1991) pp. 623–646 {{MR|1094437}} {{ZBL|}} </td></tr><tr><td valign="top">[a5]</td> <td valign="top"> E. Bishop, "Differentiable manifolds in Euclidean space" ''Duke Math. J.'' , '''32''' (1965) pp. 1–21 {{MR|200476}} {{ZBL|0154.08501}} </td></tr><tr><td valign="top">[a6]</td> <td valign="top"> S. Bu, W. Schachermayer, "Approximation of Jensen measures by image measures under holomorphic functions and applications" ''Trans. Amer. Math. Soc.'' , '''331''' (1992) pp. 585–608 {{MR|1035999}} {{ZBL|0758.46014}} </td></tr><tr><td valign="top">[a7]</td> <td valign="top"> E.M. Chirka, N.V. Shcherbina, "Pseudoconvexity of rigid domains and foliations of hulls of graphs" ''Ann. Scuola Norm. Sup. Pisa'' , '''22''' (1995) pp. 707–735 {{MR|1375316}} {{ZBL|0868.32020}} </td></tr><tr><td valign="top">[a8]</td> <td valign="top"> J. Duval, N. Sibony, "Polynomial convexity, rational convexity and currents" ''Duke Math. J.'' , '''79''' (1995) pp. 487–513 {{MR|1344768}} {{ZBL|0838.32006}} </td></tr><tr><td valign="top">[a9]</td> <td valign="top"> F. Forstnerič, "Complements of Runge domains and holomorphic hulls" ''Michigan Math. J.'' , '''41''' (1994) pp. 297–308 {{MR|1278436}} {{ZBL|0811.32007}} </td></tr><tr><td valign="top">[a10]</td> <td valign="top"> F. Forstnerič, "Polynomial hulls of sets fibered over the circle" ''Indiana Univ. Math. J.'' , '''37''' (1988) pp. 869–889 {{MR|0982834}} {{ZBL|0647.32017}} </td></tr><tr><td valign="top">[a11]</td> <td valign="top"> F. Forstnerič, E.L. Stout, "A new class of polynomially convex sets" ''Ark. Mat.'' , '''29''' (1991) pp. 51–62 {{MR|1115074}} {{ZBL|0734.32006}} </td></tr><tr><td valign="top">[a12]</td> <td valign="top"> F.R. Harvey, H.B. Lawson Jr., "On boundaries of complex analytic varieties I" ''Ann. of Math.'' , '''102''' (1975) pp. 223–290 {{MR|0425173}} {{ZBL|0317.32017}} </td></tr><tr><td valign="top">[a13]</td> <td valign="top"> L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) {{MR|0344507}} {{ZBL|0271.32001}} </td></tr><tr><td valign="top">[a14]</td> <td valign="top"> L. Hörmander, J. Wermer, "Uniform approximation on compact sets in $\mathbf{C} ^ { n }$" ''Math. Scand.'' , '''23''' (1968) pp. 5–21 {{MR|0254275}} {{ZBL|0181.36201}} </td></tr><tr><td valign="top">[a15]</td> <td valign="top"> B. Jöricke, "Local polynomial hulls of discs near isolated parabolic points" ''Indiana Univ. Math. J.'' , '''46''' : 3 (1997) pp. 789–826 {{MR|1488338}} {{ZBL|0901.32010}} </td></tr><tr><td valign="top">[a16]</td> <td valign="top"> N.G. Kruzhilin, "Two-dimensional spheres in the boundaries of strictly pseudoconvex domains in $\mathbf{C} ^ { 2 }$" ''Math. USSR Izv.'' , '''39''' (1992) pp. 1151–1187 (In Russian) {{MR|1152210}} {{ZBL|0778.32003}} </td></tr><tr><td valign="top">[a17]</td> <td valign="top"> A.G. O'Farrell, K.J. Preskenis, D. Walsh, "Holomorphic approximation in Lipschitz norms" , ''Proc. Conf. Banach Algebras and Several Complex Variables (New Haven, Conn., 1983)'' , ''Contemp. Math.'' , '''32''' (1983) pp. 187–194 {{MR|0769507}} {{ZBL|0553.32015}} </td></tr><tr><td valign="top">[a18]</td> <td valign="top"> P.J. de Paepe, "Approximation on a disk I" ''Math. Z.'' , '''212''' (1993) pp. 145–152 {{MR|}} {{ZBL|0789.30027}} </td></tr><tr><td valign="top">[a19]</td> <td valign="top"> E.A. Poletsky, "Holomorphic currents" ''Indiana Univ. Math. J.'' , '''42''' (1993) pp. 85–144 {{MR|1218708}} {{ZBL|0811.32010}} </td></tr><tr><td valign="top">[a20]</td> <td valign="top"> E.A. Poletsky, "Analytic geometry on compacta in $\mathbf{C} ^ { n }$" ''Math. Z.'' , '''222''' (1996) pp. 407–424 {{MR|1400200}} {{ZBL|0849.32009}} </td></tr><tr><td valign="top">[a21]</td> <td valign="top"> N. Shcherbina, "On the polynomial hull of a graph" ''Indiana Univ. Math. J.'' , '''42''' (1993) pp. 477–503 {{MR|1237056}} {{ZBL|0798.32026}} </td></tr><tr><td valign="top">[a22]</td> <td valign="top"> Z. Slodkowski, "Polynomial hulls with convex convex sections and interpolating spaces" ''Proc. Amer. Math. Soc.'' , '''96''' (1986) pp. 255–260 {{MR|818455}} {{ZBL|0588.32017}} </td></tr><tr><td valign="top">[a23]</td> <td valign="top"> Z. Slodkowski, "Polynomial hulls in $\mathbf{C} ^ { 2 }$ and quasi circles" ''Ann. Scuola Norm. Sup. Pisa'' , '''16''' (1989) pp. 367–391 {{MR|1050332}} {{ZBL|}} </td></tr><tr><td valign="top">[a24]</td> <td valign="top"> G. Stolzenberg, "Polynomially and rationally convex sets" ''Acta Math.'' , '''109''' (1963) pp. 259–289 {{MR|0146407}} {{ZBL|0122.08404}} </td></tr><tr><td valign="top">[a25]</td> <td valign="top"> G. Stolzenberg, "A hull with no analytic structure" ''J. Math. Mech.'' , '''12''' (1963) pp. 103–112 {{MR|0143061}} {{ZBL|0113.29101}} </td></tr><tr><td valign="top">[a26]</td> <td valign="top"> G. Stolzenberg, "Uniform approximation on smooth curves" ''Acta Math.'' , '''115''' (1966) pp. 185–198 {{MR|0192080}} {{ZBL|0143.30005}} </td></tr><tr><td valign="top">[a27]</td> <td valign="top"> E.L. Stout, "The theory of uniform algebras" , Bogden and Quigley (1971) {{MR|0423083}} {{ZBL|0286.46049}} </td></tr><tr><td valign="top">[a28]</td> <td valign="top"> B.M. Weinstock, "On the polynomial convexity of the union of two maximal totally real subspaces of $\mathbf{C} ^ { n }$" ''Math. Ann.'' , '''282''' (1988) pp. 131–138 {{MR|0960837}} {{ZBL|0628.32015}} </td></tr><tr><td valign="top">[a29]</td> <td valign="top"> J. Wermer, "Polynomial approximation on an arc in $\mathbf{C} ^ { 3 }$" ''Ann. of Math.'' , '''62''' (1955) pp. 269–270 {{MR|0072260}} {{ZBL|0067.05001}} </td></tr><tr><td valign="top">[a30]</td> <td valign="top"> J. Wermer, "The hull of a curve in $\mathbf{C} ^ { n }$" ''Ann. of Math.'' , '''68''' (1958) pp. 550–561 {{MR|0100102}} {{ZBL|0084.33402}} </td></tr><tr><td valign="top">[a31]</td> <td valign="top"> J. Wermer, "On an example of Stolzenberg" , ''Symp. Several Complex Variables, Park City, Utah'' , ''Lecture Notes in Mathematics'' , '''184''' , Springer (1970) {{MR|0298428}} {{ZBL|}} </td></tr><tr><td valign="top">[a32]</td> <td valign="top"> J. Wiegerinck, "Local polynomially convex hulls at degenerated CR singularities of surfaces in $\mathbf{C} ^ { 2 }$" ''Indiana Univ. Math. J.'' , '''44''' (1995) pp. 897–915 {{MR|1375355}} {{ZBL|0847.32013}} </td></tr></table> |
Latest revision as of 17:45, 1 July 2020
Let $\mathcal{P}$ denote the set of holomorphic polynomials on $\mathbf{C} ^ { n }$ (cf. also Analytic function). Let $K$ be a compact set in $\mathbf{C} ^ { n }$ and let $\| P \| _ { K } = \operatorname { max } _ { z \in K } | P ( z ) |$ be the sup-norm of $P \in \mathcal{P}$ on $K$. The set
\begin{equation*} \hat { K } = \{ z \in {\bf C} ^ { n } : | P ( z ) | \leq \| P \| _ { K } , \forall P \in {\cal P} \}, \end{equation*}
is called the polynomially convex hull of $K$. If $\hat { K } = K$ one says that $K$ is polynomially convex.
An up-to-date (as of 1998) text dealing with polynomial convexity is [a3], while [a13] and [a27] contain some sections on polynomial convexity, background and older results. The paper [a24] is an early study on polynomial convexity.
Polynomial convexity arises naturally in the context of function algebras (cf. also Algebra of functions): Let $P ( K )$ denote the uniform algebra generated by the holomorphic polynomials on $K$ with the sup-norm. The maximal ideal space $M$ of $P ( K )$ is the set of homomorphisms mapping $P ( K )$ onto $\mathbf{C}$, endowed with the topology inherited from the dual space $P ( K ) ^ { * }$. It can be identified with 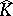 via
via
\begin{equation*} z \in \widehat { K } \leftrightarrow m _ { z }, \end{equation*}
\begin{equation*} P \mapsto P ( z ) , P \in \mathcal{P}. \end{equation*}
Moreover, if $A$ is any finitely generated function algebra on a compact Hausdorff space, then $A$ is isomorphic to $P ( K )$, where for $K$ one can take the joint spectrum of the generators of $A$ (cf. also Spectrum of an operator).
By the Riesz representation theorem (cf. Riesz theorem) there exists for every $z \in \hat { K }$ at least one representing measure $\mu _ { z }$, that is, a probability measure $\mu _ { z }$ on $K$ such that
\begin{equation*} P ( z ) = m _ { z } ( P ) = \int _ { K } P ( \zeta ) d \mu _ { z } ( \zeta ) , P \in \mathcal{P}. \end{equation*}
One calls $\mu _ { z }$ a Jensen measure if it has the stronger property
\begin{equation*} \operatorname { log } | P ( z ) | \leq \int _ { K } \operatorname { log } | P ( \zeta ) | d \mu _ { z } ( \zeta ) , P \in \mathcal{P}. \end{equation*}
It can be shown that for each $z \in \hat { K }$ there exists a Jensen measure $\mu _ { z }$. See e.g. [a27].
For compact sets $K$ in $\mathbf{C}$ one obtains 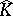 by "filling in the holes" of $K$, that is, $\hat { K } = \mathbf{C} \backslash \Omega _ { \infty }$, where $\Omega _ { \infty }$ is the unbounded component of $\mathbf{C} \backslash K$. In $\mathbf{C} ^ { n }$, $n > 1$, there is no such a simple topological description.
by "filling in the holes" of $K$, that is, $\hat { K } = \mathbf{C} \backslash \Omega _ { \infty }$, where $\Omega _ { \infty }$ is the unbounded component of $\mathbf{C} \backslash K$. In $\mathbf{C} ^ { n }$, $n > 1$, there is no such a simple topological description.
Early results on polynomial convexity, cf. [a13], are
Oka's theorem: If $K$ is a polynomially convex set in $\mathbf{C} ^ { n }$ and $f$ is holomorphic on a neighbourhood of $K$, then $f$ can be written on $K$ as a uniform limit of polynomials. Cf. also Oka theorems.
Browder's theorem: If $K$ is polynomially convex in $\mathbf{C} ^ { n }$, then $H ^ { p } ( K , {\bf C} ) = 0$ for $p \geq n$.
Here, $H ^ { p } ( K , \mathbf{C} )$ is the $p$th Čech cohomology group. More recently (1994), the following topological result was obtained, cf. [a9], [a3]:
Forstnerič' theorem: Let $K$ be a polynomially convex set in $\mathbf{C} ^ { n }$, $n \geq 2$. Then
\begin{equation*} H _ { k } ( \mathbf{C} ^ { n } \backslash K ; G ) = 0,1 \leq k \leq n - 1, \end{equation*}
and
\begin{equation*} \pi _ { k } ( \mathbf{C} ^ { n } \backslash K ) = 0,1 \leq k \leq n - 1. \end{equation*}
Here, $H _ { k } ( X , G )$ denotes the $k$th homology group of $X$ with coefficients in an Abelian group $G$ and $\pi _ { k } ( X )$ is the $k$th homotopy group of $X$.
One method to find 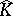 is by means of analytic discs. Let $\Delta$ be the unit disc in $\mathbf{C}$ and let $T$ be its boundary. An analytic disc is (the image of) a holomorphic mapping $f : \Delta \rightarrow {\bf C} ^ { n }$ such that $f$ is continuous up to $T$. Similarly one defines an $H ^ { \infty }$-disc as a bounded holomorphic mapping $f : \Delta \rightarrow {\bf C} ^ { n }$. Its components are elements of the usual Hardy space $H ^ { \infty } ( \Delta )$ (cf. Hardy spaces).
is by means of analytic discs. Let $\Delta$ be the unit disc in $\mathbf{C}$ and let $T$ be its boundary. An analytic disc is (the image of) a holomorphic mapping $f : \Delta \rightarrow {\bf C} ^ { n }$ such that $f$ is continuous up to $T$. Similarly one defines an $H ^ { \infty }$-disc as a bounded holomorphic mapping $f : \Delta \rightarrow {\bf C} ^ { n }$. Its components are elements of the usual Hardy space $H ^ { \infty } ( \Delta )$ (cf. Hardy spaces).
Now, let $K$ be compact in $\mathbf{C} ^ { n }$ and suppose that $f ( T ) \subset K$ for some analytic disc $f$. Then $f ( \Delta ) \subset \hat { K }$ by the maximum principle applied to $P \circ f$ for polynomials $P \in \mathcal{P}$. The same goes for $H ^ { \infty }$-discs whose boundary values are almost everywhere in $K$. One says that the disc $f$ is glued to $K$. Next, one says that 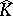 has analytic structure at $p \in \hat{K}$ if there exists a non-constant analytic disc $f$ such that $f ( 0 ) = p$ and the image of $f$ is contained in
has analytic structure at $p \in \hat{K}$ if there exists a non-constant analytic disc $f$ such that $f ( 0 ) = p$ and the image of $f$ is contained in 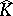 .
.
It was a major question whether $\hat{K} \backslash K$ always has analytic structure. Moreover, when is 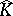 obtained by glueing discs to $K$? One positive result in this direction is due to H. Alexander [a1]; a corollary of his work is as follows: If $K$ is a rectifiable curve in $\mathbf{C} ^ { n }$, then either $\hat { K } = K$ and $P ( K ) = C ( K )$, or $\hat{K} \backslash K$ is a pure $1$-dimensional analytic subset of $\mathbf{C} ^ { n } \backslash K$ (cf. also Analytic set). If $K$ is a rectifiable arc, $K$ is polynomially convex and $P ( K ) = C ( K )$.
obtained by glueing discs to $K$? One positive result in this direction is due to H. Alexander [a1]; a corollary of his work is as follows: If $K$ is a rectifiable curve in $\mathbf{C} ^ { n }$, then either $\hat { K } = K$ and $P ( K ) = C ( K )$, or $\hat{K} \backslash K$ is a pure $1$-dimensional analytic subset of $\mathbf{C} ^ { n } \backslash K$ (cf. also Analytic set). If $K$ is a rectifiable arc, $K$ is polynomially convex and $P ( K ) = C ( K )$.
See [a1] for the complete formulation. Alexander's result is an extension of pioneering work of J. Wermer, cf. [a30], E. Bishop and, later, G. Stolzenberg [a26], who dealt with real-analytic, respectively $C ^ { 1 }$, curves. Wermer [a29] gave the first example of an arc in $\mathbf{C} ^ { 3 }$ that is not polynomially convex, cf. [a3]. However, Gel'fand's problem (i.e., let $\gamma$ be an arc in $\mathbf{C} ^ { n }$ such that $\hat{\gamma} = \gamma$; is it true that $P ( \gamma ) = C ( \gamma )$?) is still open (2000). Under the additional assumption that its projections into the complex coordinate planes have $2$-dimensional Hausdorff measure $0$, the answer is positive, see [a3].
F.R. Harvey and H.B. Lawson gave a generalization to higher-dimensional $K$, cf. [a12], which includes the following.
Let $p \geq 1$. If $K$ is a $C ^ { 2 }$ $( 2 p + 1 )$-dimensional submanifold of $\mathbf{C} ^ { n }$ and at each point of $K$ the tangent space to $K$ contains a $p$-dimensional complex subspace, then $K$ is the boundary of an analytic variety (in the sense of Stokes' theorem).
Another positive result is contained in the work of E. Bedford and W. Klingenberg, cf. [a4]: Suppose $\Gamma \subset {\bf C} ^ { 2 }$ is the graph of a $C ^ { 2 }$-function $\phi$ over the boundary of a strictly convex domain $\Omega \subset \mathbf{C} \times \mathbf{R}$. Then $\widehat{\Gamma}$ is the graph of a Lipschitz-continuous extension $\Phi$ of $\phi$ on $\Omega$. Moreover, $\widehat{\Gamma}$ is foliated with analytic discs (cf. also Foliation).
The work of Bedford and Klingenberg has been generalized in various directions in [a16], [a21] and [a7]. One ingredient of this theorem is work of Bishop [a5], which gives conditions that guarantee locally the existence of analytic discs with boundary in real submanifolds of sufficiently high dimension. See [a11], [a32] and [a15] for results along this line.
A third situation that is fairly well understood is when $K \subset \mathbf{C} ^ { n + 1 }$ is a compact set fibred over $T$, that is, $K$ is of the form $K = \{ ( z , w ) : z \in T , w \in K _ { z } \}$, where $K _ { z }$ is a compact set in $\mathbf{C} ^ { n }$ depending on $z$.
In this case the following is true: Let $K \subset \mathbf{C} ^ { 2 }$ be a compact fibration over the circle $T$ and suppose that for each $z$ the fibre $K _ { z }$ is connected and simply connected. Then $\hat{K} \backslash K$ is the union of graphs $\Gamma _ { f }$, where $f \in H ^ { \infty } ( \Delta )$ and the boundary values $f ^ { * } ( z )$ are in $K _ { z }$ for almost all $z \in T$.
Of course, it is possible that $\hat{K} \backslash K$ is empty. The present theorem is due to Z. Slodkowski, [a22], earlier results are in [a2] and [a10]. Slodkowski proved a similar theorem in $\mathbf{C} ^ { n + 1}$ under the assumption that the fibres are convex, see [a23].
Despite these positive results, in general $\hat{K} \backslash K$ need not have analytic structure. This has become clear from examples by Stolzenberg [a25] and Wermer [a31]. Presently (2000) it is not known whether 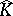 has analytic structure everywhere if $K$ is a (real) submanifold of $\mathbf{C} ^ { n }$, nor is it known under what conditions
has analytic structure everywhere if $K$ is a (real) submanifold of $\mathbf{C} ^ { n }$, nor is it known under what conditions 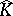 is obtained by glueing discs to $K$.
is obtained by glueing discs to $K$.
However, it has been shown that in a weaker sense there is always a kind of analytic structure in polynomial hulls. Let $d \theta$ denote Lebesgue measure on the circle $T$ and let $f ^ { * } d \theta$ denote the push-forward of $d \theta$ under a continuous mapping $f : T \rightarrow \mathbf{C} ^ { n }$. Let also $K$ be a compact set in $\mathbf{C} ^ { n }$. The following are equivalent:
1) $z \in \hat { K }$ and $\mu _ { z }$ is a Jensen measure for $z$ supported on $K$;
2) There exists a sequence of analytic discs $f _ { j } : \Delta \rightarrow \mathbf{C} ^ { n }$ such that $f _ { j } ( 0 ) \rightarrow z$ and $f _ { j } ^ { * } d \theta / 2 \pi \rightarrow \mu _ { z }$ in the weak-$*$ sense (cf. also Weak topology).
This was proved in [a6]; [a8] and [a20] contain more information about additional nice properties that can be required from the sequence of analytic discs. Under suitable regularity conditions on $K$, it is shown in [a19] that  consists of analytic discs $f$ such that $f ^ { - 1 } ( K ) \cap T$ has Lebesgue measure arbitrary close to $2 \pi$.
consists of analytic discs $f$ such that $f ^ { - 1 } ( K ) \cap T$ has Lebesgue measure arbitrary close to $2 \pi$.
Another problem is to describe $P ( K )$ assuming that $K = \hat { K }$ and given reasonable additional conditions on $K$. In particular, when can one conclude that $P ( K ) = C ( K )$? Recall that a real submanifold $M$ of $\mathbf{C} ^ { n }$ is totally real at $p \in M$ if the tangent space in $p$ does not contain a complex line (cf. also CR-submanifold). The Hörmander–Wermer theorem is as follows, cf. [a14]: Let $M$ be a sufficiently smooth real submanifold of $\mathbf{C} ^ { n }$ and let $K _ { 0 }$ be the subset of $M$ consisting of points that are not totally real. If $K \subset M$ is a compact polynomially convex set that contains an $M$-neighbourhood of $K _ { 0 }$, then $P ( K )$ contains all continuous functions on $K$ that are on $K _ { 0 }$ the uniform limit of functions holomorphic in a neighbourhood of $K _ { 0 }$.
See [a17] for a variation on this theme. One can deal with some situations where the manifold is replaced by a union of manifolds; e.g., B.M. Weinstock [a28] gives necessary and sufficient conditions for any compact subset of the union of two totally real $n$-dimensional subspaces of $\mathbf{C} ^ { n }$ to be polynomially convex; then also $P ( K ) = C ( K )$. See also [a18].
References
| [a1] | H. Alexander, "Polynomial approximation and hulls in sets of finite linear measure in $\mathbf{C} ^ { n }$" Amer J. Math. , 62 (1971) pp. 65–74 MR0284617 Zbl 0221.32011 |
| [a2] | H. Alexander, J. Wermer, "Polynomial hulls with convex fibres" Math. Ann. , 281 (1988) pp. 13–22 |
| [a3] | H. Alexander, J. Wermer, "Several complex variables and Banach algebras" , Springer (1998) MR1482798 Zbl 0894.46037 |
| [a4] | E. Bedford, W. Klingenberg Jr., "On the envelope of holomorphy of a $2$-sphere in $\mathbf{C} ^ { 2 }$" J. Amer. Math. Soc. , 4 (1991) pp. 623–646 MR1094437 |
| [a5] | E. Bishop, "Differentiable manifolds in Euclidean space" Duke Math. J. , 32 (1965) pp. 1–21 MR200476 Zbl 0154.08501 |
| [a6] | S. Bu, W. Schachermayer, "Approximation of Jensen measures by image measures under holomorphic functions and applications" Trans. Amer. Math. Soc. , 331 (1992) pp. 585–608 MR1035999 Zbl 0758.46014 |
| [a7] | E.M. Chirka, N.V. Shcherbina, "Pseudoconvexity of rigid domains and foliations of hulls of graphs" Ann. Scuola Norm. Sup. Pisa , 22 (1995) pp. 707–735 MR1375316 Zbl 0868.32020 |
| [a8] | J. Duval, N. Sibony, "Polynomial convexity, rational convexity and currents" Duke Math. J. , 79 (1995) pp. 487–513 MR1344768 Zbl 0838.32006 |
| [a9] | F. Forstnerič, "Complements of Runge domains and holomorphic hulls" Michigan Math. J. , 41 (1994) pp. 297–308 MR1278436 Zbl 0811.32007 |
| [a10] | F. Forstnerič, "Polynomial hulls of sets fibered over the circle" Indiana Univ. Math. J. , 37 (1988) pp. 869–889 MR0982834 Zbl 0647.32017 |
| [a11] | F. Forstnerič, E.L. Stout, "A new class of polynomially convex sets" Ark. Mat. , 29 (1991) pp. 51–62 MR1115074 Zbl 0734.32006 |
| [a12] | F.R. Harvey, H.B. Lawson Jr., "On boundaries of complex analytic varieties I" Ann. of Math. , 102 (1975) pp. 223–290 MR0425173 Zbl 0317.32017 |
| [a13] | L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) MR0344507 Zbl 0271.32001 |
| [a14] | L. Hörmander, J. Wermer, "Uniform approximation on compact sets in $\mathbf{C} ^ { n }$" Math. Scand. , 23 (1968) pp. 5–21 MR0254275 Zbl 0181.36201 |
| [a15] | B. Jöricke, "Local polynomial hulls of discs near isolated parabolic points" Indiana Univ. Math. J. , 46 : 3 (1997) pp. 789–826 MR1488338 Zbl 0901.32010 |
| [a16] | N.G. Kruzhilin, "Two-dimensional spheres in the boundaries of strictly pseudoconvex domains in $\mathbf{C} ^ { 2 }$" Math. USSR Izv. , 39 (1992) pp. 1151–1187 (In Russian) MR1152210 Zbl 0778.32003 |
| [a17] | A.G. O'Farrell, K.J. Preskenis, D. Walsh, "Holomorphic approximation in Lipschitz norms" , Proc. Conf. Banach Algebras and Several Complex Variables (New Haven, Conn., 1983) , Contemp. Math. , 32 (1983) pp. 187–194 MR0769507 Zbl 0553.32015 |
| [a18] | P.J. de Paepe, "Approximation on a disk I" Math. Z. , 212 (1993) pp. 145–152 Zbl 0789.30027 |
| [a19] | E.A. Poletsky, "Holomorphic currents" Indiana Univ. Math. J. , 42 (1993) pp. 85–144 MR1218708 Zbl 0811.32010 |
| [a20] | E.A. Poletsky, "Analytic geometry on compacta in $\mathbf{C} ^ { n }$" Math. Z. , 222 (1996) pp. 407–424 MR1400200 Zbl 0849.32009 |
| [a21] | N. Shcherbina, "On the polynomial hull of a graph" Indiana Univ. Math. J. , 42 (1993) pp. 477–503 MR1237056 Zbl 0798.32026 |
| [a22] | Z. Slodkowski, "Polynomial hulls with convex convex sections and interpolating spaces" Proc. Amer. Math. Soc. , 96 (1986) pp. 255–260 MR818455 Zbl 0588.32017 |
| [a23] | Z. Slodkowski, "Polynomial hulls in $\mathbf{C} ^ { 2 }$ and quasi circles" Ann. Scuola Norm. Sup. Pisa , 16 (1989) pp. 367–391 MR1050332 |
| [a24] | G. Stolzenberg, "Polynomially and rationally convex sets" Acta Math. , 109 (1963) pp. 259–289 MR0146407 Zbl 0122.08404 |
| [a25] | G. Stolzenberg, "A hull with no analytic structure" J. Math. Mech. , 12 (1963) pp. 103–112 MR0143061 Zbl 0113.29101 |
| [a26] | G. Stolzenberg, "Uniform approximation on smooth curves" Acta Math. , 115 (1966) pp. 185–198 MR0192080 Zbl 0143.30005 |
| [a27] | E.L. Stout, "The theory of uniform algebras" , Bogden and Quigley (1971) MR0423083 Zbl 0286.46049 |
| [a28] | B.M. Weinstock, "On the polynomial convexity of the union of two maximal totally real subspaces of $\mathbf{C} ^ { n }$" Math. Ann. , 282 (1988) pp. 131–138 MR0960837 Zbl 0628.32015 |
| [a29] | J. Wermer, "Polynomial approximation on an arc in $\mathbf{C} ^ { 3 }$" Ann. of Math. , 62 (1955) pp. 269–270 MR0072260 Zbl 0067.05001 |
| [a30] | J. Wermer, "The hull of a curve in $\mathbf{C} ^ { n }$" Ann. of Math. , 68 (1958) pp. 550–561 MR0100102 Zbl 0084.33402 |
| [a31] | J. Wermer, "On an example of Stolzenberg" , Symp. Several Complex Variables, Park City, Utah , Lecture Notes in Mathematics , 184 , Springer (1970) MR0298428 |
| [a32] | J. Wiegerinck, "Local polynomially convex hulls at degenerated CR singularities of surfaces in $\mathbf{C} ^ { 2 }$" Indiana Univ. Math. J. , 44 (1995) pp. 897–915 MR1375355 Zbl 0847.32013 |
Polynomial convexity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Polynomial_convexity&oldid=14374