Difference between revisions of "Partition"
(Importing text file) |
(MSC 54B, 11P) |
||
| Line 1: | Line 1: | ||
| + | {{MSC|54B}} | ||
| + | ==Of a topological space== | ||
A closed set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p0717401.png" /> in a topological space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p0717402.png" /> that partitions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p0717403.png" /> between two given sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p0717404.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p0717405.png" /> (or, in other words, separates <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p0717406.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p0717407.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p0717408.png" />), i.e. such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p0717409.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174010.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174011.png" /> are disjoint and open in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174012.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174013.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174014.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174015.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174016.png" /> are open in all of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174017.png" />). A partition is called fine if its interior is empty. Any binary [[Decomposition|decomposition]] (i.e. a partition consisting of two elements) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174018.png" /> of a space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174019.png" /> defines a fine partition in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174020.png" />: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174021.png" /> is the boundary of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174022.png" />, which is the boundary of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174023.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174024.png" />, in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174025.png" /> is the open kernel (cf. [[Kernel of a set|Kernel of a set]]) of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174026.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174027.png" />. The converse is also true. In essence, the concept of a partition between sets leads to the concept of connectedness. The converse also applies: A space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174028.png" /> is disconnected if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174029.png" /> is a partition between non-empty sets. | A closed set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p0717401.png" /> in a topological space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p0717402.png" /> that partitions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p0717403.png" /> between two given sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p0717404.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p0717405.png" /> (or, in other words, separates <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p0717406.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p0717407.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p0717408.png" />), i.e. such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p0717409.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174010.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174011.png" /> are disjoint and open in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174012.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174013.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174014.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174015.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174016.png" /> are open in all of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174017.png" />). A partition is called fine if its interior is empty. Any binary [[Decomposition|decomposition]] (i.e. a partition consisting of two elements) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174018.png" /> of a space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174019.png" /> defines a fine partition in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174020.png" />: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174021.png" /> is the boundary of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174022.png" />, which is the boundary of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174023.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174024.png" />, in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174025.png" /> is the open kernel (cf. [[Kernel of a set|Kernel of a set]]) of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174026.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174027.png" />. The converse is also true. In essence, the concept of a partition between sets leads to the concept of connectedness. The converse also applies: A space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174028.png" /> is disconnected if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174029.png" /> is a partition between non-empty sets. | ||
| Line 12: | Line 14: | ||
One readily sees that every partition is a separator and that every separator is a cut, and the following examples show that the notions are in general distinct: the open interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174048.png" /> is a separator between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174049.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174050.png" /> in the interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174051.png" />, but not a partition; in the well-known subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174052.png" /> of the Euclidean space, the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174053.png" /> is a cut but not a separator between the points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174054.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174055.png" />. | One readily sees that every partition is a separator and that every separator is a cut, and the following examples show that the notions are in general distinct: the open interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174048.png" /> is a separator between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174049.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174050.png" /> in the interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174051.png" />, but not a partition; in the well-known subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174052.png" /> of the Euclidean space, the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174053.png" /> is a cut but not a separator between the points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174054.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174055.png" />. | ||
| + | {{MSC|11P}} | ||
| + | ==Of a positive integer== | ||
A partition of a positive integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174056.png" /> is a decomposition of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174057.png" /> as a sum of positive integers. For example, the partitions of 4 read: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174058.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174059.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174060.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174061.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174062.png" />. The number of different partitions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174063.png" /> is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174064.png" />. So, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174065.png" />. L. Euler gave a non-trivial recurrence relation for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174066.png" /> (see [[#References|[a1]]]) and Ramanujan discovered the surprising congruences <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174067.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174068.png" />), <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174069.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174070.png" />), <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174071.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174072.png" />), and others. He also found the asymptotic relation | A partition of a positive integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174056.png" /> is a decomposition of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174057.png" /> as a sum of positive integers. For example, the partitions of 4 read: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174058.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174059.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174060.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174061.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174062.png" />. The number of different partitions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174063.png" /> is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174064.png" />. So, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174065.png" />. L. Euler gave a non-trivial recurrence relation for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174066.png" /> (see [[#References|[a1]]]) and Ramanujan discovered the surprising congruences <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174067.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174068.png" />), <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174069.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174070.png" />), <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174071.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174072.png" />), and others. He also found the asymptotic relation | ||
Revision as of 18:26, 21 November 2014
2020 Mathematics Subject Classification: Primary: 54B [MSN][ZBL]
Of a topological space
A closed set 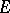 in a topological space
in a topological space 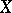 that partitions
that partitions 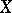 between two given sets
between two given sets 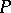 and
and 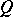 (or, in other words, separates
(or, in other words, separates 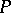 and
and 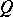 in
in 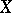 ), i.e. such that
), i.e. such that 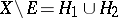 , where
, where 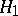 and
and 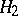 are disjoint and open in
are disjoint and open in 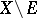 ,
, 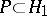 ,
, 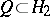 (
(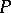 and
and 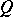 are open in all of
are open in all of 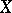 ). A partition is called fine if its interior is empty. Any binary decomposition (i.e. a partition consisting of two elements)
). A partition is called fine if its interior is empty. Any binary decomposition (i.e. a partition consisting of two elements) 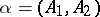 of a space
of a space 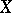 defines a fine partition in
defines a fine partition in 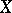 :
: 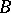 is the boundary of
is the boundary of 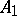 , which is the boundary of
, which is the boundary of 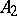 , where
, where 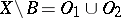 , in which
, in which 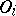 is the open kernel (cf. Kernel of a set) of
is the open kernel (cf. Kernel of a set) of 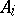 ,
, 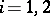 . The converse is also true. In essence, the concept of a partition between sets leads to the concept of connectedness. The converse also applies: A space
. The converse is also true. In essence, the concept of a partition between sets leads to the concept of connectedness. The converse also applies: A space 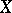 is disconnected if
is disconnected if 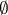 is a partition between non-empty sets.
is a partition between non-empty sets.
Comments
Related notions in this context are those of a separator and of a cut.
If 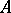 and
and 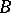 are disjoint subsets of a space
are disjoint subsets of a space 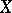 , then a separator between
, then a separator between 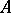 and
and 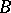 is a set
is a set 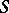 such that
such that 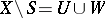 with
with 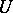 and
and 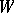 disjoint and open in
disjoint and open in 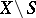 , and
, and 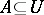 and
and 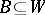 . So a partition is a closed separator.
. So a partition is a closed separator.
A set 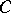 is a cut between
is a cut between 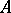 and
and 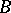 if
if 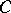 intersects every continuum that intersects both
intersects every continuum that intersects both 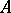 and
and 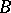 .
.
One readily sees that every partition is a separator and that every separator is a cut, and the following examples show that the notions are in general distinct: the open interval 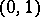 is a separator between
is a separator between 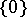 and
and 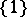 in the interval
in the interval 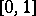 , but not a partition; in the well-known subspace
, but not a partition; in the well-known subspace 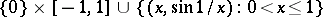 of the Euclidean space, the point
of the Euclidean space, the point 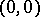 is a cut but not a separator between the points
is a cut but not a separator between the points 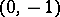 and
and 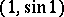 .
.
2020 Mathematics Subject Classification: Primary: 11P [MSN][ZBL]
Of a positive integer
A partition of a positive integer  is a decomposition of
is a decomposition of  as a sum of positive integers. For example, the partitions of 4 read:
as a sum of positive integers. For example, the partitions of 4 read: 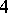 ,
, 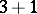 ,
, 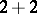 ,
, 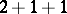 ,
, 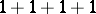 . The number of different partitions of
. The number of different partitions of  is denoted by
is denoted by 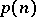 . So,
. So, 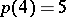 . L. Euler gave a non-trivial recurrence relation for
. L. Euler gave a non-trivial recurrence relation for 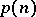 (see [a1]) and Ramanujan discovered the surprising congruences
(see [a1]) and Ramanujan discovered the surprising congruences 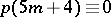 (
(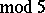 ),
), 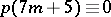 (
(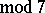 ),
), 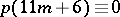 (
(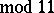 ), and others. He also found the asymptotic relation
), and others. He also found the asymptotic relation
 |
where 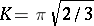 . Later this was completed to an exact series expansion by H. Rademacher (see [a2]).
. Later this was completed to an exact series expansion by H. Rademacher (see [a2]).
One can also distinguish other partitions, having particular properties, such as the numbers in the decomposition being distinct (see [a3]). See also Additive number theory; Additive problems.
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapt. XVI |
| [a2] | T.M. Apostol, "Modular functions and Dirichlet series in number theory" , Springer (1976) |
| [a3] | G.E. Andrews, "The theory of partitions" , Addison-Wesley (1976) |
| [a4] | R. Engelking, "Dimension theory" , North-Holland & PWN (1978) pp. 19; 50 |
Partition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Partition&oldid=34709