Difference between revisions of "Parabolic cylinder function"
(Importing text file) |
m (fixing linebreak) |
||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | p0711901.png | ||
| + | $#A+1 = 36 n = 1 | ||
| + | $#C+1 = 36 : ~/encyclopedia/old_files/data/P071/P.0701190 Parabolic cylinder function, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''Weber function, Weber–Hermite function'' | ''Weber function, Weber–Hermite function'' | ||
A solution of the differential equation | A solution of the differential equation | ||
| − | + | $$ \tag{* } | |
| + | |||
| + | \frac{d ^ {2} y }{dz ^ {2} } | ||
| + | + \left ( \nu + | ||
| + | \frac{1}{2} | ||
| + | - | ||
| + | \frac{z ^ {2} }{4} | ||
| + | \right ) y | ||
| + | = 0, | ||
| + | $$ | ||
| + | |||
| + | which is obtained as a result of separating the variables in the [[Wave equation|wave equation]] $ \Delta u = k ^ {2} u $ | ||
| + | in parabolic cylindrical coordinates (cf. [[Parabolic coordinates|Parabolic coordinates]]). Ordinarily one uses the solution | ||
| + | |||
| + | $$ | ||
| + | D _ \nu ( z) \equiv U \left ( - \nu - | ||
| + | \frac{1}{2} | ||
| + | , z \right ) = \ | ||
| + | 2 ^ {( \nu - 1)/2 } e ^ {- z ^ {2} /4 } \Psi \left ( | ||
| + | \frac{1 - \nu }{2} | ||
| + | , | ||
| + | \frac{3}{2} | ||
| + | ; \ | ||
| + | |||
| + | \frac{z ^ {2} }{2} | ||
| + | \right ) , | ||
| + | $$ | ||
| − | + | where $ \Psi ( a, b; z) $ | |
| + | is the [[Confluent hypergeometric function|confluent hypergeometric function]]. The functions $ D _ \nu (- z) $ | ||
| + | and $ D _ {- \nu - 1 } (\pm iz) $ | ||
| + | also satisfy equation (*). The functions $ D _ \nu ( z) $ | ||
| + | and $ D _ {- \nu - 1 } (\pm iz) $ | ||
| + | are linearly independent for arbitrary $ \nu $, | ||
| + | and $ D _ \nu ( z) $ | ||
| + | and $ D _ \nu (- z) $ | ||
| + | are linearly independent for $ \nu \neq 0, \pm 1 , \dots $. | ||
| + | The parabolic cylinder functions are entire functions of $ z $. | ||
| + | The function $ D _ \nu ( z) $ | ||
| + | is real for real $ \nu $ | ||
| + | and $ z $. | ||
| − | + | The differentiation formulas are, $ n = 1, 2 ,\dots $: | |
| − | + | $$ | |
| − | + | \frac{d ^ {n} }{dz ^ {n} } | |
| + | \left [ e ^ {z ^ {2} /4 } D _ \nu ( z) \right ] = \ | ||
| + | (- 1) ^ {n} (- \nu ) _ {n} e ^ {z ^ {2} /4 } D _ {\nu - n } ( z), | ||
| + | $$ | ||
| − | + | $$ | |
| − | + | \frac{d ^ {n} }{dz ^ {n} } | |
| + | \left [ e ^ {- z ^ {2} /4 } D _ \nu ( z) | ||
| + | \right ] = (- 1) ^ {n} e ^ {- z ^ {2} /4 } D _ {\nu + n } ( z) . | ||
| + | $$ | ||
The recurrence formulas are: | The recurrence formulas are: | ||
| − | + | $$ | |
| + | D _ {\nu + 1 } ( z) - zD _ \nu ( z) + \nu D _ {\nu - 1 } ( z) = 0, | ||
| + | $$ | ||
| − | + | $$ | |
| + | D _ \nu ^ \prime ( z) + | ||
| + | \frac{z}{2} | ||
| + | D _ \nu ( z) - \nu D _ {\nu - 1 } ( z) = 0, | ||
| + | $$ | ||
| − | + | $$ | |
| + | D _ \nu ^ \prime ( z) - | ||
| + | \frac{z}{2} | ||
| + | D _ \nu ( z) + D _ {\nu + 1 } ( z) = 0. | ||
| + | $$ | ||
| − | Asymptotically, for fixed | + | Asymptotically, for fixed $ \nu $ |
| + | and $ | \mathop{\rm arg} z | < 3 \pi /4 $, | ||
| + | as $ z \rightarrow \infty $, | ||
| + | one has | ||
| − | + | $$ | |
| + | D _ \nu ( z) = \ | ||
| + | z ^ \nu e ^ {- z ^ {2} /4 } \left [ \sum _ { k= 0} ^ { N } | ||
| + | \frac{(- \nu /2) _ {k} ( 1/2 | ||
| + | - \nu /2) _ {k} }{k!} | ||
| + | \left ( | ||
| + | \frac{z ^ {2} }{- 2} | ||
| + | \right ) ^ {- k}\right .+ | ||
| + | \left . | ||
| + | O ( | z | ^ {- 2N- 2 } ) \right ] , | ||
| + | $$ | ||
| − | + | and, for bounded $ | z | $ | |
| + | and $ | \mathop{\rm arg} ( - \nu ) | \leq \pi /2 $, | ||
| + | as $ | \nu | \rightarrow \infty $, | ||
| + | one has | ||
| − | + | $$ | |
| + | D _ \nu ( z) = \ | ||
| − | + | \frac{1}{\sqrt 2 } | |
| + | \mathop{\rm exp} \left [ | ||
| + | \frac \nu {2} | ||
| + | \mathop{\rm ln} (- \nu ) - | ||
| + | \frac \nu {2} | ||
| + | - \sqrt {- \nu } z | ||
| + | \right ] | ||
| + | \left [ 1 + O \left ( | ||
| + | \frac{1}{\sqrt {| \nu | } } | ||
| + | \right ) \right ] . | ||
| + | $$ | ||
| − | + | Parabolic cylinder functions are related to other functions as follows ($ n = 0, 1 , \dots $): | |
| + | To the [[Hermite polynomials|Hermite polynomials]] by | ||
| − | + | $$ | |
| + | D _ {n} ( z) = \ | ||
| + | 2 ^ {- n/2} e ^ {- z ^ {2} /4 } H _ {n} \left ( | ||
| + | \frac{z}{\sqrt 2} | ||
| + | \right ) , | ||
| + | $$ | ||
| − | + | to the [[Probability integral|probability integral]] (error function) by | |
| − | + | $$ | |
| + | D _ {-} n- 1 ( z) = \ | ||
| − | + | \frac{(- 1) ^ {n} \sqrt 2 }{n!} | |
| + | e ^ {- z ^ {2} /4 } | ||
| + | \frac{d ^ {n} }{dz ^ {n} } | ||
| + | \left | ||
| + | ( e ^ {z ^ {2} /3 } \mathop{\rm erfc} | ||
| + | \frac{z}{\sqrt z } | ||
| + | \right ) , | ||
| + | $$ | ||
and to the [[Bessel functions|Bessel functions]] by | and to the [[Bessel functions|Bessel functions]] by | ||
| − | + | $$ | |
| + | D _ {- 1/2} ( z) = \ | ||
| + | \sqrt { | ||
| + | \frac{\pi z }{2} | ||
| + | } K _ {1/4} \left ( | ||
| + | \frac{z ^ {2} }{4} | ||
| + | \right ) . | ||
| + | $$ | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Bateman (ed.) A. Erdélyi (ed.) et al. (ed.) , ''Higher transcendental functions'' , '''2. Bessel functions, parabolic cylinder functions, orthogonal polynomials''' , McGraw-Hill (1953)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.C.P. Miller, "Giving solutions of the differential equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071190/p07119037.png" />, tables of Weber parabolic cylinder functions" , H.M. Stationary Office (1955)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Bateman (ed.) A. Erdélyi (ed.) et al. (ed.) , ''Higher transcendental functions'' , '''2. Bessel functions, parabolic cylinder functions, orthogonal polynomials''' , McGraw-Hill (1953)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.C.P. Miller, "Giving solutions of the differential equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071190/p07119037.png" />, tables of Weber parabolic cylinder functions" , H.M. Stationary Office (1955)</TD></TR></table> | ||
Latest revision as of 02:24, 22 April 2022
Weber function, Weber–Hermite function
A solution of the differential equation
$$ \tag{* } \frac{d ^ {2} y }{dz ^ {2} } + \left ( \nu + \frac{1}{2} - \frac{z ^ {2} }{4} \right ) y = 0, $$
which is obtained as a result of separating the variables in the wave equation $ \Delta u = k ^ {2} u $ in parabolic cylindrical coordinates (cf. Parabolic coordinates). Ordinarily one uses the solution
$$ D _ \nu ( z) \equiv U \left ( - \nu - \frac{1}{2} , z \right ) = \ 2 ^ {( \nu - 1)/2 } e ^ {- z ^ {2} /4 } \Psi \left ( \frac{1 - \nu }{2} , \frac{3}{2} ; \ \frac{z ^ {2} }{2} \right ) , $$
where $ \Psi ( a, b; z) $ is the confluent hypergeometric function. The functions $ D _ \nu (- z) $ and $ D _ {- \nu - 1 } (\pm iz) $ also satisfy equation (*). The functions $ D _ \nu ( z) $ and $ D _ {- \nu - 1 } (\pm iz) $ are linearly independent for arbitrary $ \nu $, and $ D _ \nu ( z) $ and $ D _ \nu (- z) $ are linearly independent for $ \nu \neq 0, \pm 1 , \dots $. The parabolic cylinder functions are entire functions of $ z $. The function $ D _ \nu ( z) $ is real for real $ \nu $ and $ z $.
The differentiation formulas are, $ n = 1, 2 ,\dots $:
$$ \frac{d ^ {n} }{dz ^ {n} } \left [ e ^ {z ^ {2} /4 } D _ \nu ( z) \right ] = \ (- 1) ^ {n} (- \nu ) _ {n} e ^ {z ^ {2} /4 } D _ {\nu - n } ( z), $$
$$ \frac{d ^ {n} }{dz ^ {n} } \left [ e ^ {- z ^ {2} /4 } D _ \nu ( z) \right ] = (- 1) ^ {n} e ^ {- z ^ {2} /4 } D _ {\nu + n } ( z) . $$
The recurrence formulas are:
$$ D _ {\nu + 1 } ( z) - zD _ \nu ( z) + \nu D _ {\nu - 1 } ( z) = 0, $$
$$ D _ \nu ^ \prime ( z) + \frac{z}{2} D _ \nu ( z) - \nu D _ {\nu - 1 } ( z) = 0, $$
$$ D _ \nu ^ \prime ( z) - \frac{z}{2} D _ \nu ( z) + D _ {\nu + 1 } ( z) = 0. $$
Asymptotically, for fixed $ \nu $ and $ | \mathop{\rm arg} z | < 3 \pi /4 $, as $ z \rightarrow \infty $, one has
$$ D _ \nu ( z) = \ z ^ \nu e ^ {- z ^ {2} /4 } \left [ \sum _ { k= 0} ^ { N } \frac{(- \nu /2) _ {k} ( 1/2 - \nu /2) _ {k} }{k!} \left ( \frac{z ^ {2} }{- 2} \right ) ^ {- k}\right .+ \left . O ( | z | ^ {- 2N- 2 } ) \right ] , $$
and, for bounded $ | z | $ and $ | \mathop{\rm arg} ( - \nu ) | \leq \pi /2 $, as $ | \nu | \rightarrow \infty $, one has
$$ D _ \nu ( z) = \ \frac{1}{\sqrt 2 } \mathop{\rm exp} \left [ \frac \nu {2} \mathop{\rm ln} (- \nu ) - \frac \nu {2} - \sqrt {- \nu } z \right ] \left [ 1 + O \left ( \frac{1}{\sqrt {| \nu | } } \right ) \right ] . $$
Parabolic cylinder functions are related to other functions as follows ($ n = 0, 1 , \dots $): To the Hermite polynomials by
$$ D _ {n} ( z) = \ 2 ^ {- n/2} e ^ {- z ^ {2} /4 } H _ {n} \left ( \frac{z}{\sqrt 2} \right ) , $$
to the probability integral (error function) by
$$ D _ {-} n- 1 ( z) = \ \frac{(- 1) ^ {n} \sqrt 2 }{n!} e ^ {- z ^ {2} /4 } \frac{d ^ {n} }{dz ^ {n} } \left ( e ^ {z ^ {2} /3 } \mathop{\rm erfc} \frac{z}{\sqrt z } \right ) , $$
and to the Bessel functions by
$$ D _ {- 1/2} ( z) = \ \sqrt { \frac{\pi z }{2} } K _ {1/4} \left ( \frac{z ^ {2} }{4} \right ) . $$
References
| [1] | H. Bateman (ed.) A. Erdélyi (ed.) et al. (ed.) , Higher transcendental functions , 2. Bessel functions, parabolic cylinder functions, orthogonal polynomials , McGraw-Hill (1953) |
| [2] | J.C.P. Miller, "Giving solutions of the differential equation 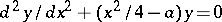 , tables of Weber parabolic cylinder functions" , H.M. Stationary Office (1955) , tables of Weber parabolic cylinder functions" , H.M. Stationary Office (1955) |
Parabolic cylinder function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Parabolic_cylinder_function&oldid=13870