Difference between revisions of "Nuclear space"
(Importing text file) |
m (fixing hat) |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | n0678601.png | ||
| + | $#A+1 = 308 n = 1 | ||
| + | $#C+1 = 308 : ~/encyclopedia/old_files/data/N067/N.0607860 Nuclear space | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
A [[Locally convex space|locally convex space]] for which all continuous linear mappings into an arbitrary Banach space are nuclear operators (cf. [[Nuclear operator|Nuclear operator]]). The concept of a nuclear space arose [[#References|[1]]] in an investigation of the question: For what spaces are the analogues of Schwartz' kernel theorem valid (see [[Nuclear bilinear form|Nuclear bilinear form]])? The fundamental results in the theory of nuclear spaces are due to A. Grothendieck [[#References|[1]]]. The function spaces used in analysis are, as a rule, Banach or nuclear spaces. Nuclear spaces play an important role in the spectral analysis of operators on Hilbert spaces (the construction of rigged Hilbert spaces, expansions in terms of generalized eigen vectors, etc.) (see [[#References|[2]]]). Nuclear spaces are closely connected with measure theory on locally convex spaces (see [[#References|[3]]]). Nuclear spaces can be characterized in terms of dimension-type invariants (approximative dimension, diametral dimension, etc.) (see [[#References|[2]]], [[#References|[4]]], [[#References|[5]]]). One of these invariants is the functional dimension, which for many spaces consisting of entire analytic functions is the same as the number of variables on which these functions depend (see [[#References|[2]]]). | A [[Locally convex space|locally convex space]] for which all continuous linear mappings into an arbitrary Banach space are nuclear operators (cf. [[Nuclear operator|Nuclear operator]]). The concept of a nuclear space arose [[#References|[1]]] in an investigation of the question: For what spaces are the analogues of Schwartz' kernel theorem valid (see [[Nuclear bilinear form|Nuclear bilinear form]])? The fundamental results in the theory of nuclear spaces are due to A. Grothendieck [[#References|[1]]]. The function spaces used in analysis are, as a rule, Banach or nuclear spaces. Nuclear spaces play an important role in the spectral analysis of operators on Hilbert spaces (the construction of rigged Hilbert spaces, expansions in terms of generalized eigen vectors, etc.) (see [[#References|[2]]]). Nuclear spaces are closely connected with measure theory on locally convex spaces (see [[#References|[3]]]). Nuclear spaces can be characterized in terms of dimension-type invariants (approximative dimension, diametral dimension, etc.) (see [[#References|[2]]], [[#References|[4]]], [[#References|[5]]]). One of these invariants is the functional dimension, which for many spaces consisting of entire analytic functions is the same as the number of variables on which these functions depend (see [[#References|[2]]]). | ||
| Line 5: | Line 17: | ||
===Examples of nuclear spaces.=== | ===Examples of nuclear spaces.=== | ||
| + | 1) Let $ {\mathcal E} ( \mathbf R ^ {n} ) $ | ||
| + | be the space of all (real or complex) infinitely-differentiable functions on $ \mathbf R ^ {n} $ | ||
| + | equipped with the topology of uniform convergence of all derivatives on compact subsets of $ \mathbf R ^ {n} $. | ||
| + | The space $ {\mathcal E} ^ \prime ( \mathbf R ^ {n} ) $ | ||
| + | dual to $ {\mathcal E} ( \mathbf R ^ {n} ) $ | ||
| + | consists of all generalized functions (cf. [[Generalized function|Generalized function]]) with compact support. Let $ {\mathcal D} ( \mathbf R ^ {n} ) $ | ||
| + | and $ {\mathcal S} ( \mathbf R ^ {n} ) $ | ||
| + | be the linear subspaces of $ {\mathcal E} ( \mathbf R ^ {n} ) $ | ||
| + | consisting, respectively, of functions with compact support and of functions that, together with all their derivatives, decrease faster than any power of $ | x | ^ {- 1} $ | ||
| + | as $ | x | \rightarrow \infty $. | ||
| + | The duals $ {\mathcal D} ^ \prime ( \mathbf R ^ {n} ) $ | ||
| + | and $ {\mathcal S} ^ \prime ( \mathbf R ^ {n} ) $ | ||
| + | of $ {\mathcal D} ( \mathbf R ^ {n} ) $ | ||
| + | and $ {\mathcal S} ( \mathbf R ^ {n} ) $, | ||
| + | relative to the standard topology, consist of all generalized functions and of all generalized functions of slow growth, respectively. The spaces $ {\mathcal E} $, | ||
| + | $ {\mathcal D} $, | ||
| + | $ {\mathcal S} $, | ||
| + | $ {\mathcal E} ^ \prime $, | ||
| + | $ {\mathcal D} ^ \prime $, | ||
| + | and $ {\mathcal S} ^ \prime $, | ||
| + | equipped with the strong topology, are complete reflexive nuclear spaces. | ||
| − | + | 2) let $ \{ a _ {np} \} $ | |
| − | + | be an infinite matrix, where $ 0 \leq a _ {np} < \infty $ | |
| − | + | and $ a _ {np} \leq a _ {n ( p + 1) } $, | |
| + | $ n, p = 1, 2 , . . . $. | ||
| + | The space of sequences $ \xi = \{ \xi _ {n} \} $ | ||
| + | for which $ | \xi | _ {p} = \sum _ {n = 0 } ^ \infty | \xi _ {n} | a _ {np} < \infty $ | ||
| + | for all $ p $, | ||
| + | with the topology defined by the semi-norms $ \xi \rightarrow | \xi | _ {p} $ (cf. [[Semi-norm|Semi-norm]]), is called a Köthe space, and is denoted by $ {\mathcal K} ( a _ {np} ) $. | ||
| + | This space is nuclear if and only if for any $ p $ | ||
| + | one can find a $ q $ | ||
| + | such that $ \sum _ {n = 0 } ^ \infty ( a _ {np} /a _ {nq} ) < \infty $. | ||
==Heredity properties.== | ==Heredity properties.== | ||
A locally convex space is nuclear if and only if its completion is nuclear. Every subspace (separable quotient space) of a nuclear space is nuclear. The direct sum, the inductive limit of a countable family of nuclear spaces, and also the product and the projective limit of any family of nuclear spaces, is again nuclear. | A locally convex space is nuclear if and only if its completion is nuclear. Every subspace (separable quotient space) of a nuclear space is nuclear. The direct sum, the inductive limit of a countable family of nuclear spaces, and also the product and the projective limit of any family of nuclear spaces, is again nuclear. | ||
| − | Let | + | Let $ E $ |
| + | be an arbitrary locally convex space, and let $ E ^ \prime $ | ||
| + | denote its dual equipped with the strong topology. If $ E ^ \prime $ | ||
| + | is nuclear, then $ E $ | ||
| + | is called conuclear. If $ E $ | ||
| + | is arbitrary and $ F $ | ||
| + | is a nuclear space, then the space $ L ( E, F ) $ | ||
| + | of continuous linear operators from $ E $ | ||
| + | into $ F $ | ||
| + | is nuclear with respect to the strong [[Operator topology|operator topology]] (simple convergence); if $ E $ | ||
| + | is semi-reflexive and conuclear, then $ L ( E, F ) $ | ||
| + | is nuclear also in the topology of bounded convergence. | ||
==Metric and dually-metric nuclear spaces.== | ==Metric and dually-metric nuclear spaces.== | ||
| − | A locally convex space | + | A locally convex space $ E $ |
| + | is called dually metric, or a space of type $ ( {\mathcal D} {\mathcal F} ) $, | ||
| + | if it has a countable fundamental system of bounded sets and if every (strongly) bounded countable union of equicontinuous subsets in $ E ^ \prime $ | ||
| + | is equicontinuous (cf. [[Equicontinuity|Equicontinuity]]). Any strong dual of a metrizable locally convex space is dually metric; the converse is not true. If $ E $ | ||
| + | is a space of type $ ( {\mathcal D} {\mathcal F} ) $, | ||
| + | then $ E ^ \prime $ | ||
| + | is of type $ ( {\mathcal F} ) $ (a Fréchet space, that is, complete and metrizable). Examples of nuclear spaces of type $ ( {\mathcal F} ) $ | ||
| + | are Köthe spaces, and also $ {\mathcal E} $ | ||
| + | and $ {\mathcal S} $; | ||
| + | accordingly, $ {\mathcal E} ^ \prime $ | ||
| + | and $ {\mathcal S} ^ \prime $ | ||
| + | are nuclear spaces of type $ ( {\mathcal D} {\mathcal F} ) $. | ||
| + | The spaces $ {\mathcal D} $ | ||
| + | and $ {\mathcal D} ^ \prime $ | ||
| + | are neither metric nor dually metric. | ||
| − | Metric and dually-metric nuclear spaces are separable, and if complete, they are reflexive. The transition | + | Metric and dually-metric nuclear spaces are separable, and if complete, they are reflexive. The transition $ E \rightarrow E ^ \prime $ |
| + | to the dual space establishes a one-to-one correspondence between nuclear spaces of type $ ( {\mathcal F} ) $ | ||
| + | and complete nuclear spaces of type $ ( {\mathcal D} {\mathcal F} ) $. | ||
| + | If $ E $ | ||
| + | is a complete nuclear space of type $ ( {\mathcal D} {\mathcal F} ) $ | ||
| + | and if $ F $ | ||
| + | is a nuclear space of type $ ( {\mathcal F} ) $, | ||
| + | then $ L ( E, F ) $, | ||
| + | equipped with the topology of bounded convergence, is nuclear and conuclear. | ||
| − | Every nuclear space of type | + | Every nuclear space of type $ ( {\mathcal F} ) $ |
| + | is isomorphic to a subspace of the space $ {\mathcal E} ( \mathbf R ) $ | ||
| + | of infinitely-differentiable functions on the real line, that is, $ {\mathcal E} ( \mathbf R ) $ | ||
| + | is a universal space for the nuclear spaces of type $ ( {\mathcal F} ) $ (see [[#References|[10]]]). A Fréchet space $ E $ | ||
| + | is nuclear if and only if every unconditionally-convergent series (cf. [[Unconditional convergence|Unconditional convergence]]) in $ E $ | ||
| + | is absolutely convergent (that is, with respect to any continuous semi-norm). Spaces of holomorphic functions on nuclear spaces of types $ ( {\mathcal F} ) $ | ||
| + | and $ ( {\mathcal D} {\mathcal F} ) $ | ||
| + | have been studied intensively (see [[#References|[11]]]). | ||
==Tensor products of nuclear spaces, and spaces of vector functions.== | ==Tensor products of nuclear spaces, and spaces of vector functions.== | ||
| − | The algebraic tensor product | + | The algebraic tensor product $ E \otimes F $ |
| + | of two locally convex spaces $ E $ | ||
| + | and $ F $ | ||
| + | can be equipped with the projective and injective topologies, and then $ E \otimes F $ | ||
| + | becomes a topological tensor product. The projective topology is the strongest locally convex topology in which the canonical bilinear mapping $ E \times F \rightarrow E \otimes F $ | ||
| + | is continuous. The injective topology (or the topology of (bi) equicontinuous convergence) is induced by the natural imbedding $ E \otimes F \rightarrow L _ {e} ( E _ \tau ^ \prime , F ) $, | ||
| + | where $ E _ \tau ^ \prime $ | ||
| + | is the dual of $ E $ | ||
| + | equipped with the [[Mackey topology|Mackey topology]] $ \tau ( E ^ \prime , E) $, | ||
| + | and $ L _ {e} ( E _ \tau ^ \prime , F ) $ | ||
| + | is the space of continuous linear mappings $ E _ \tau ^ \prime \rightarrow F $ | ||
| + | equipped with the topology of [[Uniform convergence|uniform convergence]] on equicontinuous sets in $ E ^ \prime $. | ||
| + | Under this imbedding $ x \otimes y \in E \otimes F $ | ||
| + | goes into the operator $ x ^ \prime \mapsto \langle x, x ^ \prime \rangle y $, | ||
| + | where $ \langle x, x ^ \prime \rangle $ | ||
| + | denotes the value of the functional $ x ^ \prime \in E ^ \prime $ | ||
| + | at $ x \in E $. | ||
| + | The completion of $ E \otimes F $ | ||
| + | in the projective (respectively, injective) topology is denoted by $ E \widehat \otimes F $ (respectively, $ E \widetilde \otimes F $). | ||
| − | For | + | For $ E $ |
| + | to be a nuclear space it is necessary and sufficient that for any locally convex space $ F $ | ||
| + | the projective and injective topologies in $ E \otimes F $ | ||
| + | coincide, that is, | ||
| − | + | $$ \tag{1 } | |
| + | E \widehat \otimes F = E \widetilde \otimes F. | ||
| + | $$ | ||
| − | Actually, it suffices to require that (1) holds for | + | Actually, it suffices to require that (1) holds for $ F = l _ {1} $, |
| + | the space of summable sequences, or for $ F $ | ||
| + | equal to a fixed space with an unconditional basis (see [[#References|[12]]]). Nevertheless, there is a (non-nuclear) infinite-dimensional separable Banach space $ X $ | ||
| + | such that $ X \widehat \otimes X = X \widetilde \otimes X $ (see [[#References|[13]]]). If $ E $ | ||
| + | and $ F $ | ||
| + | are complete spaces and $ F $ | ||
| + | is nuclear, then the imbedding $ E \otimes F \rightarrow L _ {e} ( E _ \tau ^ \prime , F ) $ | ||
| + | can be extended to an isomorphism between $ E \widehat \otimes F $ | ||
| + | and $ L _ {e} ( E _ \tau ^ \prime , F ) $. | ||
| − | If | + | If $ E $ |
| + | is a non-null nuclear space, then $ E \widehat \otimes F $ | ||
| + | is nuclear if and only if $ F $ | ||
| + | is nuclear. If $ E $ | ||
| + | and $ F $ | ||
| + | are both spaces of type $ ( {\mathcal F} ) $ (or $ ( {\mathcal D} {\mathcal F} ) $) | ||
| + | and if $ E $ | ||
| + | is nuclear, then $ ( E \widehat \otimes F ) ^ \prime = E ^ \prime \widehat \otimes F ^ \prime $. | ||
| − | Let | + | Let $ E $ |
| + | be a complete nuclear space consisting of scalar functions (not all) on a certain set $ T $; | ||
| + | let also $ E $ | ||
| + | be the inductive limit (locally convex hull) of a countable sequence of spaces of type $ ( {\mathcal F} ) $, | ||
| + | and let the topology on $ E $ | ||
| + | be not weaker than the topology of pointwise convergence of functions on $ T $. | ||
| + | Then for any complete space $ F $ | ||
| + | one can identify $ E \widehat \otimes F $ | ||
| + | with the space of all mappings (vector functions) $ T \rightarrow F $ | ||
| + | for which the scalar function $ t \mapsto \langle f ( t), y ^ \prime \rangle $ | ||
| + | belongs to $ E $ | ||
| + | for all $ y ^ \prime \in F ^ { \prime } $. | ||
| + | In particular, $ {\mathcal E} ( \mathbf R ^ {n} ) \widehat \otimes F $ | ||
| + | coincides with the space of all infinitely-differentiable vector functions on $ \mathbf R ^ {n} $ | ||
| + | with values in $ F $, | ||
| + | and $ {\mathcal E} ( \mathbf R ^ {n} ) \widehat \otimes {\mathcal E} ( \mathbf R ^ {m} ) = {\mathcal E} ( \mathbf R ^ {n} \times \mathbf R ^ {m} ) = {\mathcal E} ( \mathbf R ^ {n + m } ) $. | ||
==The structure of nuclear spaces.== | ==The structure of nuclear spaces.== | ||
| − | Let | + | Let $ U $ |
| + | be a convex circled (i.e. convex balanced) neighbourhood of zero in a locally convex space $ E $, | ||
| + | and let $ p $ | ||
| + | be the Minkowski functional (continuous semi-norm) corresponding to $ U $. | ||
| + | Let $ E _ {U} $ | ||
| + | be the quotient space $ E/p ^ {- 1 }( 0) $ | ||
| + | with the norm induced by $ p $, | ||
| + | and let $ \widehat {E _ {U} } $ | ||
| + | be the completion of the normed space $ E _ {U} $. | ||
| + | There is defined a continuous canonical linear mapping $ E \rightarrow \widehat {E _ {U} } $; | ||
| + | if $ U $ | ||
| + | contains a neighbourhood $ V $, | ||
| + | then the continuous linear mapping $ \widehat{E _ {V} } \rightarrow \widehat{E _ {U} } $ | ||
| + | is defined canonically. | ||
| − | For a locally convex space | + | For a locally convex space $ E $ |
| + | the following conditions are equivalent: 1) $ E $ | ||
| + | is nuclear; 2) $ E $ | ||
| + | has a basis $ \mathfrak B $ | ||
| + | of convex circled neighbourhoods of zero such that for any $ U \in \mathfrak B $ | ||
| + | the canonical mapping $ E \rightarrow \widehat{E _ {U} } $ | ||
| + | is a nuclear operator; 3) the mapping $ E \rightarrow \widehat{E _ {U} } $ | ||
| + | is nuclear for any convex circled neighbourhood $ U $ | ||
| + | of zero in $ E $; | ||
| + | and 4) every convex circled neighbourhood $ U $ | ||
| + | of zero in $ E $ | ||
| + | contains another such neighbourhood of zero, $ V $, | ||
| + | such that the canonical mapping $ \widehat {E _ {V} } \rightarrow \widehat{E _ {U} } $ | ||
| + | is nuclear. | ||
| − | Let | + | Let $ E $ |
| + | be a nuclear space. For any neighbourhood $ U $ | ||
| + | of zero in $ E $ | ||
| + | and for any $ q $ | ||
| + | such that $ 1 \leq q \leq \infty $ | ||
| + | there is a convex circled neighbourhood $ V \subset U $ | ||
| + | for which $ E _ {V} $ | ||
| + | is (norm) isomorphic to a subspace of the space $ l _ {q} $ | ||
| + | of sequences with summable $ q $-th powers. Thus, $ E $ | ||
| + | coincides with a subspace of the projective limit of a family of spaces isomorphic to $ l _ {q} $. | ||
| + | In particular (the case $ q = 2 $), | ||
| + | in any nuclear space $ E $ | ||
| + | there is a basis of neighbourhoods of zero $ \{ U _ \alpha \} $ | ||
| + | such that all the spaces $ \widehat{E _ {U _ \alpha } } $ | ||
| + | are Hilbert spaces; thus, $ E $ | ||
| + | is Hilbertian, that is, the topology in $ E $ | ||
| + | can be generated by a family of semi-norms each of which is obtained from a certain non-negative definite Hermitian form on $ E \times E $. | ||
| + | Any complete nuclear space is isomorphic to the projective limit of a family of Hilbert spaces. A space $ E $ | ||
| + | of type $ ( {\mathcal F} ) $ | ||
| + | is nuclear if and only if it can be represented as the projective limit $ E = \lim\limits _ \leftarrow g _ {mn} H _ {n} $ | ||
| + | of a countable family of Hilbert spaces $ H _ {n} $, | ||
| + | such that the $ g _ {mn} $ | ||
| + | are nuclear operators (or, at least, Hilbert–Schmidt operators, cf. [[Hilbert–Schmidt operator|Hilbert–Schmidt operator]]) for $ m < n $. | ||
==Bases in nuclear spaces.== | ==Bases in nuclear spaces.== | ||
| − | In a nuclear space every equicontinuous basis is absolute. In a space of type | + | In a nuclear space every equicontinuous basis is absolute. In a space of type $ ( {\mathcal F} ) $ |
| + | any countable basis (even if weak) is an equicontinuous Schauder basis (cf. [[Basis|Basis]]), so that in a nuclear space of type $ ( {\mathcal F} ) $ | ||
| + | any basis is absolute (in particular, unconditional). A similar result holds for complete nuclear spaces of type $ ( {\mathcal D} {\mathcal F} ) $, | ||
| + | and for all nuclear spaces for which the [[Closed-graph theorem|closed-graph theorem]] holds. A quotient space of a nuclear space of type $ ( {\mathcal F} ) $ | ||
| + | with a basis does not necessarily have a basis (see [[#References|[4]]], [[#References|[5]]], [[#References|[6]]]). | ||
| − | Let | + | Let $ E $ |
| + | be a nuclear space of type $ ( {\mathcal F} ) $. | ||
| + | A topology can be defined in $ E $ | ||
| + | by a countable system of semi-norms $ x \mapsto \| x \| _ {q} $, | ||
| + | $ q = 1, 2 \dots $ | ||
| + | where $ \| x \| _ {q} \leq \| x \| _ {q + 1 } $ | ||
| + | for all $ x \in E $. | ||
| + | If $ E $ | ||
| + | has a basis or a continuous norm, then the semi-norms $ \| \cdot \| $ | ||
| + | can be taken as norms. Let $ \{ e _ {n} \} $ | ||
| + | be a basis in $ E $; | ||
| + | then any $ x \in E $ | ||
| + | can be expressed as an (absolutely and unconditionally) convergent series | ||
| − | + | $$ | |
| + | x = \ | ||
| + | \sum _ {n = 1 } ^ \infty | ||
| + | \xi _ {n} e _ {n} , | ||
| + | $$ | ||
| − | where the coordinates | + | where the coordinates $ \xi _ {n} $ |
| + | have the form $ \xi _ {n} = \langle x, x _ {n} ^ \prime \rangle $, | ||
| + | and the functionals $ x _ {n} ^ \prime $ | ||
| + | form a bi-orthogonal basis in $ E ^ \prime $. | ||
| + | $ E $ | ||
| + | is isomorphic to the Köthe space $ {\mathcal K} ( a _ {nq} ) $, | ||
| + | where $ a _ {nq} = \| e _ {n} \| _ {q} $; | ||
| + | under this isomorphism $ x \in E $ | ||
| + | goes into the sequence $ \{ \xi _ {n} \} $ | ||
| + | of its coordinates. A basis $ \{ f _ {n} \} $ | ||
| + | in $ E $ | ||
| + | is equivalent to the basis $ \{ e _ {n} \} $ (that is, it can be obtained from $ \{ e _ {n} \} $ | ||
| + | by an isomorphism) if and only if $ {\mathcal K} ( \| e _ {n} \| _ {q} ) $ | ||
| + | and $ {\mathcal K} ( \| f _ {n} \| _ {q} ) $ | ||
| + | coincide as sets [[#References|[4]]]. A basis $ \{ f _ {n} \} $ | ||
| + | is called regular (or proper) if there is a system of norms $ \| \cdot \| _ {q} $ | ||
| + | and a permutation $ \sigma $ | ||
| + | of indices such that $ \| f _ {\sigma ( n) } \| _ {q} / \| f _ {\sigma ( n) } \| _ {r} $ | ||
| + | is monotone decreasing for all $ r \geq q $. | ||
| + | If a nuclear space $ E $ | ||
| + | of type $ ( {\mathcal F} ) $ | ||
| + | has a regular basis, then any two bases in $ E $ | ||
| + | are quasi-equivalent (that is, they can be made equivalent by a permutation and a normalization of the elements of one of them). There are other sufficient conditions for all bases in $ E $ | ||
| + | to be quasi-equivalent (see [[#References|[4]]], [[#References|[14]]]). A complete description of the class of nuclear spaces with this property is not known (1984). | ||
| − | Example. The Hermite functions | + | Example. The Hermite functions $ \phi _ {n} ( t) = e ^ {t ^ {2} /2 } ( {d ^ {n} } / {dt ^ {n} } ) ( e ^ {- t ^ {2} } ) $ |
| + | form a basis in the complete metric nuclear space $ {\mathcal S} ( \mathbf R ) $ | ||
| + | of smooth functions on the real line that are rapidly decreasing together with all their derivatives. $ {\mathcal S} ( \mathbf R ) $ | ||
| + | is isomorphic to $ {\mathcal K} ( n ^ {p} ) $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Grothendieck, "Produits tensoriels topologiques et espaces nucléaires" , Amer. Math. Soc. (1955)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.M. Gel'fand, N.Ya. Vilenkin, "Generalized functions. Applications of harmonic analysis" , '''4''' , Acad. Press (1968) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> R.A. Minlos, "Generalized random processes and their extension in measure" ''Trudy Moskov. Mat. Obshch.'' , '''8''' (1959) pp. 497–518 (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> B.S. Mityagin, "Approximate dimension and bases in nuclear spaces" ''Russian Math. Surveys'' , '''16''' : 4 pp. 59–127 ''Uspekhi Mat. Nauk'' , '''16''' : 4 (1961) pp. 63–132</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> A. Pietsch, "Nuclear locally convex spaces" , Springer (1972) (Translated from German)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> E. Dubinsky, "Structure of nuclear Fréchet spaces" , Springer (1979)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> N.M. Zobin, B.S. Mityagin, "Examples of nuclear linear metric spaces without a basis" ''Funct. Anal. Appl.'' , '''8''' : 4 (1974) pp. 304–313 ''Funktsional. Anal. i Prilozhen.'' , '''8''' : 4 (1974) pp. 35–47</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> A. Atzmon, "An operator without invariant subspaces on a nuclear Fréchet space" ''Ann. of Math.'' , '''117''' : 3 (1983) pp. 669–694</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> H.H. Schaefer, "Topological vector spaces" , Springer (1971)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> T. Komura, Y. Komura, "Ueber die Einbettung der nuklearen Räume in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067860/n067860231.png" />" ''Math. Ann.'' , '''162''' (1965–1966) pp. 284–288</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> S. Dineen, "Complex analysis in locally convex spaces" , North-Holland (1981)</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> K. John, V. Zizler, "On a tensor product characterization of nuclearity" ''Math. Ann.'' , '''244''' : 1 (1979) pp. 83–87</TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> G. Pisier, "Contre-example à une conjecture de Grothendieck" ''C.R. Acad. Sci. Paris'' , '''293''' (1981) pp. 681–683 (English abstract)</TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> M.M. Dragilev, "Bases in Köthe spaces" , Rostov-on-Don (1983) (In Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Grothendieck, "Produits tensoriels topologiques et espaces nucléaires" , Amer. Math. Soc. (1955)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.M. Gel'fand, N.Ya. Vilenkin, "Generalized functions. Applications of harmonic analysis" , '''4''' , Acad. Press (1968) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> R.A. Minlos, "Generalized random processes and their extension in measure" ''Trudy Moskov. Mat. Obshch.'' , '''8''' (1959) pp. 497–518 (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> B.S. Mityagin, "Approximate dimension and bases in nuclear spaces" ''Russian Math. Surveys'' , '''16''' : 4 pp. 59–127 ''Uspekhi Mat. Nauk'' , '''16''' : 4 (1961) pp. 63–132</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> A. Pietsch, "Nuclear locally convex spaces" , Springer (1972) (Translated from German)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> E. Dubinsky, "Structure of nuclear Fréchet spaces" , Springer (1979)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> N.M. Zobin, B.S. Mityagin, "Examples of nuclear linear metric spaces without a basis" ''Funct. Anal. Appl.'' , '''8''' : 4 (1974) pp. 304–313 ''Funktsional. Anal. i Prilozhen.'' , '''8''' : 4 (1974) pp. 35–47</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> A. Atzmon, "An operator without invariant subspaces on a nuclear Fréchet space" ''Ann. of Math.'' , '''117''' : 3 (1983) pp. 669–694</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> H.H. Schaefer, "Topological vector spaces" , Springer (1971)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> T. Komura, Y. Komura, "Ueber die Einbettung der nuklearen Räume in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067860/n067860231.png" />" ''Math. Ann.'' , '''162''' (1965–1966) pp. 284–288</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> S. Dineen, "Complex analysis in locally convex spaces" , North-Holland (1981)</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> K. John, V. Zizler, "On a tensor product characterization of nuclearity" ''Math. Ann.'' , '''244''' : 1 (1979) pp. 83–87</TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> G. Pisier, "Contre-example à une conjecture de Grothendieck" ''C.R. Acad. Sci. Paris'' , '''293''' (1981) pp. 681–683 (English abstract)</TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> M.M. Dragilev, "Bases in Köthe spaces" , Rostov-on-Don (1983) (In Russian)</TD></TR></table> | ||
| + | ====Comments==== | ||
| + | A generalized function is also called a distribution, and a generalized function of slow growth is also called a tempered distribution. | ||
| + | Let $ F $ | ||
| + | be a topological linear space, $ U $ | ||
| + | a neighbourhood of zero in $ F $, | ||
| + | $ A $ | ||
| + | a set in $ F $, | ||
| + | and $ \epsilon $ | ||
| + | a (small) positive number. An $ \epsilon $-set for $ A $ | ||
| + | relative to a neighbourhood $ U $ | ||
| + | of zero is a set $ B $ | ||
| + | such that for every $ a \in A $ | ||
| + | there is a $ b \in B $ | ||
| + | such that $ a \in b + \epsilon U $. | ||
| + | Let $ N ( \epsilon , A , U ) $ | ||
| + | be the smallest number of elements in $ \epsilon $-sets for $ A $ | ||
| + | relative to $ U $. | ||
| + | The functional dimension of $ F $ | ||
| + | is defined by | ||
| − | = | + | $$ |
| − | + | \mathop{\rm df} ( F ) = \sup _ { U } \inf _ { V } \ | |
| + | {\lim\limits \sup } _ {\epsilon \rightarrow 0 } \ | ||
| − | + | \frac{ { \mathop{\rm ln} \mathop{\rm ln} } N ( \epsilon , V , U ) }{ { \mathop{\rm ln} \mathop{\rm ln} } \epsilon ^ {- 1} } | |
| + | , | ||
| + | $$ | ||
| − | + | where $ U , V $ | |
| + | range over the neighbourhoods of zero in $ F $. | ||
| + | Cf. [[#References|[2]]], Sect. I.3.8 for more details. | ||
| − | + | Let $ F $ | |
| + | be a locally convex space and consider two neighbourhoods of zero $ U , V $ | ||
| + | such that $ U $ | ||
| + | absorbs $ V $, | ||
| + | i.e. $ V \subset \rho U $ | ||
| + | for some positive number $ \rho $. | ||
| + | Let | ||
| − | + | $$ | |
| + | \delta _ {r} ( U , V ) = \inf \{ \delta : \exists \ | ||
| + | \textrm{ subspace } G \textrm{ of dimension } \leq r | ||
| + | $$ | ||
| − | + | $$ | |
| + | {} \textrm{ such that } V \subset \delta U + G \} . | ||
| + | $$ | ||
| − | + | This number is called the $ r $-th diameter of $ V $ | |
| + | with respect to $ U $. | ||
| + | The diametral dimension of a locally convex space is the collection of all sequences $ ( d _ {r} ) _ {r \in \mathbf N \cup \{ 0 \} } $ | ||
| + | of non-negative numbers with the property that for each neighbourhood of zero $ U $ | ||
| + | there is a neighbourhood $ V $ | ||
| + | of zero absorbed by $ U $ | ||
| + | for which $ \delta _ {r} ( U , V ) \leq d _ {r} $, | ||
| + | $ r \in \mathbf N \cup \{ 0 \} $. | ||
| − | + | A locally convex space $ E $ | |
| + | is nuclear if and only if for some (respectively, each) positive number $ \lambda $ | ||
| + | the sequence $ ( ( r + 1 ) ^ {- \lambda } ) _ {r \in N \cup \{ 0 \} } $ | ||
| + | belongs to the diametral dimension of $ E $. | ||
| + | See [[#References|[5]]], Chapt. 9 for more details. | ||
| − | + | Let again $ U , V $ | |
| + | be neighbourhoods of zero of a locally convex space $ F $ | ||
| + | such that $ U $ | ||
| + | absorbs $ V $. | ||
| + | The $ \epsilon $-content of $ V $ | ||
| + | with respect to $ U $ | ||
| + | is the supremum $ M _ \epsilon ( U , V ) $ | ||
| + | of all natural numbers $ m $ | ||
| + | such that there are $ x _ {1} \dots x _ {m} \in V $ | ||
| + | with $ x _ {1} \dots x _ {k} \notin \epsilon U $ | ||
| + | for all $ i \neq k $. | ||
| + | The approximative dimension of a locally convex space $ F $ | ||
| + | is the collection of all positive functions $ \phi $ | ||
| + | on $ ( 0 , \infty ) $ | ||
| + | such that for each neighbourhood $ U $ | ||
| + | of zero there is a neighbourhood $ V $ | ||
| + | of zero absorbed by $ U $ | ||
| + | such that | ||
| − | + | $$ | |
| + | \lim\limits _ {\epsilon \rightarrow 0 } \phi ( \epsilon ) ^ {- 1} | ||
| + | M _ \epsilon ( U , V ) = 0 . | ||
| + | $$ | ||
| − | + | The number $ \rho ( U , V ) $ | |
| + | is defined by the exponential rate of growth of $ M _ \epsilon ( U , V ) $ | ||
| + | as $ \epsilon \rightarrow 0 $. | ||
| + | More precisely, | ||
| − | + | $$ | |
| + | \rho ( U , V ) = {\lim\limits \sup } _ {\epsilon \rightarrow 0 } \ | ||
| − | + | \frac{ { \mathop{\rm ln} \mathop{\rm ln} } M _ \epsilon ( U , V ) }{ \mathop{\rm ln} \epsilon ^ {- 1} } | |
| + | . | ||
| + | $$ | ||
| − | A locally convex space | + | A locally convex space $ E $ |
| + | is nuclear if and only if for some (respectively, each) positive number $ \rho $ | ||
| + | the following condition is satisfied: For each neighbourhood of zero $ U $ | ||
| + | there is a neighbourhood $ V $ | ||
| + | of zero absorbed by $ U $ | ||
| + | such that $ \rho ( U , V ) \leq \rho $. | ||
| + | Cf. [[#References|[5]]], Chapt. 9 for more details. | ||
| − | Let | + | Let $ U $ |
| + | be a bounded circled neighbourhood of a topological vector space $ F $. | ||
| + | The Minkowski functional associated to $ U $ | ||
| + | is defined by | ||
| − | + | $$ | |
| + | q ( x) = \inf _ {x \in \alpha U } \alpha ,\ \ | ||
| + | \alpha \geq 0 . | ||
| + | $$ | ||
| − | This is well-defined for each | + | This is well-defined for each $ x $ |
| + | since $ U $ | ||
| + | is absorbent (i.e. for each $ x \in F $ | ||
| + | there is an $ \alpha $ | ||
| + | such that $ x \in \alpha U $). | ||
| + | Cf. [[#References|[a7]]], Sects. 15.10, 16.4. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Grothendieck, "Résumé de la théorie métrique des produits tensoriels topologiques" ''Bol. Soc. Mat. Sao-Paulo'' , '''8''' (1956) pp. 1–79</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Grothendieck, "Topological vector spaces" , Gordon & Breach (1973) (Translated from French)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> H. Jarchow, "Locally convex spaces" , Teubner (1981) (Translated from German)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> G. Pisier, "Factorization of linear operators and geometry of Banach spaces" , Amer. Math. Soc. (1986)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> G. Pisier, "Counterexamples to a conjecture of Grothendieck" ''Acta. Math.'' , '''151''' (1983) pp. 181–208</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> J.F. Colombeau, "Differential calculus and holomorphy" , North-Holland (1982)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> G. Köthe, "Topological vector spaces" , '''1''' , Springer (1969)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Grothendieck, "Résumé de la théorie métrique des produits tensoriels topologiques" ''Bol. Soc. Mat. Sao-Paulo'' , '''8''' (1956) pp. 1–79</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Grothendieck, "Topological vector spaces" , Gordon & Breach (1973) (Translated from French)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> H. Jarchow, "Locally convex spaces" , Teubner (1981) (Translated from German)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> G. Pisier, "Factorization of linear operators and geometry of Banach spaces" , Amer. Math. Soc. (1986)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> G. Pisier, "Counterexamples to a conjecture of Grothendieck" ''Acta. Math.'' , '''151''' (1983) pp. 181–208</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> J.F. Colombeau, "Differential calculus and holomorphy" , North-Holland (1982)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> G. Köthe, "Topological vector spaces" , '''1''' , Springer (1969)</TD></TR></table> | ||
Latest revision as of 07:00, 6 May 2022
A locally convex space for which all continuous linear mappings into an arbitrary Banach space are nuclear operators (cf. Nuclear operator). The concept of a nuclear space arose [1] in an investigation of the question: For what spaces are the analogues of Schwartz' kernel theorem valid (see Nuclear bilinear form)? The fundamental results in the theory of nuclear spaces are due to A. Grothendieck [1]. The function spaces used in analysis are, as a rule, Banach or nuclear spaces. Nuclear spaces play an important role in the spectral analysis of operators on Hilbert spaces (the construction of rigged Hilbert spaces, expansions in terms of generalized eigen vectors, etc.) (see [2]). Nuclear spaces are closely connected with measure theory on locally convex spaces (see [3]). Nuclear spaces can be characterized in terms of dimension-type invariants (approximative dimension, diametral dimension, etc.) (see [2], [4], [5]). One of these invariants is the functional dimension, which for many spaces consisting of entire analytic functions is the same as the number of variables on which these functions depend (see [2]).
In their properties, nuclear spaces are close to finite-dimensional spaces. Every bounded set in a nuclear space is pre-compact. If a nuclear space is complete (or at least quasi-complete, that is, every closed bounded set is complete), then it is semi-reflexive (that is, the space coincides with its second dual as a set of elements), and every closed bounded set in it is compact. If a quasi-complete nuclear space is a barrelled space, then it is also a Montel space (in particular, a reflexive space); any weakly-convergent countable sequence in this space converges also in the original topology. A normed space is nuclear if and only if it is finite dimensional. Every nuclear space has the approximation property: Any continuous linear operator in such a space can be approximated in the operator topology of pre-compact convergence by operators of finite rank (that is, continuous linear operators with finite-dimensional ranges). Nevertheless, there are nuclear Fréchet spaces (cf. Fréchet space) that do not have the bounded approximation property; in such a space the identity operator is not the limit of a countable sequence of operators of finite rank in the strong or weak operator topology [6]. Nuclear Fréchet spaces without a Schauder basis have been constructed, and they can have arbitrarily small diametral dimension, that is, they can be arbitrarily near (in a certain sense) to finite-dimensional spaces [7]. For nuclear spaces a counterexample to the problem of invariant subspaces has been constructed: In a certain nuclear Fréchet space one can find a continuous linear operator without non-trivial invariant closed subspaces [8].
Examples of nuclear spaces.
1) Let $ {\mathcal E} ( \mathbf R ^ {n} ) $ be the space of all (real or complex) infinitely-differentiable functions on $ \mathbf R ^ {n} $ equipped with the topology of uniform convergence of all derivatives on compact subsets of $ \mathbf R ^ {n} $. The space $ {\mathcal E} ^ \prime ( \mathbf R ^ {n} ) $ dual to $ {\mathcal E} ( \mathbf R ^ {n} ) $ consists of all generalized functions (cf. Generalized function) with compact support. Let $ {\mathcal D} ( \mathbf R ^ {n} ) $ and $ {\mathcal S} ( \mathbf R ^ {n} ) $ be the linear subspaces of $ {\mathcal E} ( \mathbf R ^ {n} ) $ consisting, respectively, of functions with compact support and of functions that, together with all their derivatives, decrease faster than any power of $ | x | ^ {- 1} $ as $ | x | \rightarrow \infty $. The duals $ {\mathcal D} ^ \prime ( \mathbf R ^ {n} ) $ and $ {\mathcal S} ^ \prime ( \mathbf R ^ {n} ) $ of $ {\mathcal D} ( \mathbf R ^ {n} ) $ and $ {\mathcal S} ( \mathbf R ^ {n} ) $, relative to the standard topology, consist of all generalized functions and of all generalized functions of slow growth, respectively. The spaces $ {\mathcal E} $, $ {\mathcal D} $, $ {\mathcal S} $, $ {\mathcal E} ^ \prime $, $ {\mathcal D} ^ \prime $, and $ {\mathcal S} ^ \prime $, equipped with the strong topology, are complete reflexive nuclear spaces.
2) let $ \{ a _ {np} \} $ be an infinite matrix, where $ 0 \leq a _ {np} < \infty $ and $ a _ {np} \leq a _ {n ( p + 1) } $, $ n, p = 1, 2 , . . . $. The space of sequences $ \xi = \{ \xi _ {n} \} $ for which $ | \xi | _ {p} = \sum _ {n = 0 } ^ \infty | \xi _ {n} | a _ {np} < \infty $ for all $ p $, with the topology defined by the semi-norms $ \xi \rightarrow | \xi | _ {p} $ (cf. Semi-norm), is called a Köthe space, and is denoted by $ {\mathcal K} ( a _ {np} ) $. This space is nuclear if and only if for any $ p $ one can find a $ q $ such that $ \sum _ {n = 0 } ^ \infty ( a _ {np} /a _ {nq} ) < \infty $.
Heredity properties.
A locally convex space is nuclear if and only if its completion is nuclear. Every subspace (separable quotient space) of a nuclear space is nuclear. The direct sum, the inductive limit of a countable family of nuclear spaces, and also the product and the projective limit of any family of nuclear spaces, is again nuclear.
Let $ E $ be an arbitrary locally convex space, and let $ E ^ \prime $ denote its dual equipped with the strong topology. If $ E ^ \prime $ is nuclear, then $ E $ is called conuclear. If $ E $ is arbitrary and $ F $ is a nuclear space, then the space $ L ( E, F ) $ of continuous linear operators from $ E $ into $ F $ is nuclear with respect to the strong operator topology (simple convergence); if $ E $ is semi-reflexive and conuclear, then $ L ( E, F ) $ is nuclear also in the topology of bounded convergence.
Metric and dually-metric nuclear spaces.
A locally convex space $ E $ is called dually metric, or a space of type $ ( {\mathcal D} {\mathcal F} ) $, if it has a countable fundamental system of bounded sets and if every (strongly) bounded countable union of equicontinuous subsets in $ E ^ \prime $ is equicontinuous (cf. Equicontinuity). Any strong dual of a metrizable locally convex space is dually metric; the converse is not true. If $ E $ is a space of type $ ( {\mathcal D} {\mathcal F} ) $, then $ E ^ \prime $ is of type $ ( {\mathcal F} ) $ (a Fréchet space, that is, complete and metrizable). Examples of nuclear spaces of type $ ( {\mathcal F} ) $ are Köthe spaces, and also $ {\mathcal E} $ and $ {\mathcal S} $; accordingly, $ {\mathcal E} ^ \prime $ and $ {\mathcal S} ^ \prime $ are nuclear spaces of type $ ( {\mathcal D} {\mathcal F} ) $. The spaces $ {\mathcal D} $ and $ {\mathcal D} ^ \prime $ are neither metric nor dually metric.
Metric and dually-metric nuclear spaces are separable, and if complete, they are reflexive. The transition $ E \rightarrow E ^ \prime $ to the dual space establishes a one-to-one correspondence between nuclear spaces of type $ ( {\mathcal F} ) $ and complete nuclear spaces of type $ ( {\mathcal D} {\mathcal F} ) $. If $ E $ is a complete nuclear space of type $ ( {\mathcal D} {\mathcal F} ) $ and if $ F $ is a nuclear space of type $ ( {\mathcal F} ) $, then $ L ( E, F ) $, equipped with the topology of bounded convergence, is nuclear and conuclear.
Every nuclear space of type $ ( {\mathcal F} ) $ is isomorphic to a subspace of the space $ {\mathcal E} ( \mathbf R ) $ of infinitely-differentiable functions on the real line, that is, $ {\mathcal E} ( \mathbf R ) $ is a universal space for the nuclear spaces of type $ ( {\mathcal F} ) $ (see [10]). A Fréchet space $ E $ is nuclear if and only if every unconditionally-convergent series (cf. Unconditional convergence) in $ E $ is absolutely convergent (that is, with respect to any continuous semi-norm). Spaces of holomorphic functions on nuclear spaces of types $ ( {\mathcal F} ) $ and $ ( {\mathcal D} {\mathcal F} ) $ have been studied intensively (see [11]).
Tensor products of nuclear spaces, and spaces of vector functions.
The algebraic tensor product $ E \otimes F $ of two locally convex spaces $ E $ and $ F $ can be equipped with the projective and injective topologies, and then $ E \otimes F $ becomes a topological tensor product. The projective topology is the strongest locally convex topology in which the canonical bilinear mapping $ E \times F \rightarrow E \otimes F $ is continuous. The injective topology (or the topology of (bi) equicontinuous convergence) is induced by the natural imbedding $ E \otimes F \rightarrow L _ {e} ( E _ \tau ^ \prime , F ) $, where $ E _ \tau ^ \prime $ is the dual of $ E $ equipped with the Mackey topology $ \tau ( E ^ \prime , E) $, and $ L _ {e} ( E _ \tau ^ \prime , F ) $ is the space of continuous linear mappings $ E _ \tau ^ \prime \rightarrow F $ equipped with the topology of uniform convergence on equicontinuous sets in $ E ^ \prime $. Under this imbedding $ x \otimes y \in E \otimes F $ goes into the operator $ x ^ \prime \mapsto \langle x, x ^ \prime \rangle y $, where $ \langle x, x ^ \prime \rangle $ denotes the value of the functional $ x ^ \prime \in E ^ \prime $ at $ x \in E $. The completion of $ E \otimes F $ in the projective (respectively, injective) topology is denoted by $ E \widehat \otimes F $ (respectively, $ E \widetilde \otimes F $).
For $ E $ to be a nuclear space it is necessary and sufficient that for any locally convex space $ F $ the projective and injective topologies in $ E \otimes F $ coincide, that is,
$$ \tag{1 } E \widehat \otimes F = E \widetilde \otimes F. $$
Actually, it suffices to require that (1) holds for $ F = l _ {1} $, the space of summable sequences, or for $ F $ equal to a fixed space with an unconditional basis (see [12]). Nevertheless, there is a (non-nuclear) infinite-dimensional separable Banach space $ X $ such that $ X \widehat \otimes X = X \widetilde \otimes X $ (see [13]). If $ E $ and $ F $ are complete spaces and $ F $ is nuclear, then the imbedding $ E \otimes F \rightarrow L _ {e} ( E _ \tau ^ \prime , F ) $ can be extended to an isomorphism between $ E \widehat \otimes F $ and $ L _ {e} ( E _ \tau ^ \prime , F ) $.
If $ E $ is a non-null nuclear space, then $ E \widehat \otimes F $ is nuclear if and only if $ F $ is nuclear. If $ E $ and $ F $ are both spaces of type $ ( {\mathcal F} ) $ (or $ ( {\mathcal D} {\mathcal F} ) $) and if $ E $ is nuclear, then $ ( E \widehat \otimes F ) ^ \prime = E ^ \prime \widehat \otimes F ^ \prime $.
Let $ E $ be a complete nuclear space consisting of scalar functions (not all) on a certain set $ T $; let also $ E $ be the inductive limit (locally convex hull) of a countable sequence of spaces of type $ ( {\mathcal F} ) $, and let the topology on $ E $ be not weaker than the topology of pointwise convergence of functions on $ T $. Then for any complete space $ F $ one can identify $ E \widehat \otimes F $ with the space of all mappings (vector functions) $ T \rightarrow F $ for which the scalar function $ t \mapsto \langle f ( t), y ^ \prime \rangle $ belongs to $ E $ for all $ y ^ \prime \in F ^ { \prime } $. In particular, $ {\mathcal E} ( \mathbf R ^ {n} ) \widehat \otimes F $ coincides with the space of all infinitely-differentiable vector functions on $ \mathbf R ^ {n} $ with values in $ F $, and $ {\mathcal E} ( \mathbf R ^ {n} ) \widehat \otimes {\mathcal E} ( \mathbf R ^ {m} ) = {\mathcal E} ( \mathbf R ^ {n} \times \mathbf R ^ {m} ) = {\mathcal E} ( \mathbf R ^ {n + m } ) $.
The structure of nuclear spaces.
Let $ U $ be a convex circled (i.e. convex balanced) neighbourhood of zero in a locally convex space $ E $, and let $ p $ be the Minkowski functional (continuous semi-norm) corresponding to $ U $. Let $ E _ {U} $ be the quotient space $ E/p ^ {- 1 }( 0) $ with the norm induced by $ p $, and let $ \widehat {E _ {U} } $ be the completion of the normed space $ E _ {U} $. There is defined a continuous canonical linear mapping $ E \rightarrow \widehat {E _ {U} } $; if $ U $ contains a neighbourhood $ V $, then the continuous linear mapping $ \widehat{E _ {V} } \rightarrow \widehat{E _ {U} } $ is defined canonically.
For a locally convex space $ E $ the following conditions are equivalent: 1) $ E $ is nuclear; 2) $ E $ has a basis $ \mathfrak B $ of convex circled neighbourhoods of zero such that for any $ U \in \mathfrak B $ the canonical mapping $ E \rightarrow \widehat{E _ {U} } $ is a nuclear operator; 3) the mapping $ E \rightarrow \widehat{E _ {U} } $ is nuclear for any convex circled neighbourhood $ U $ of zero in $ E $; and 4) every convex circled neighbourhood $ U $ of zero in $ E $ contains another such neighbourhood of zero, $ V $, such that the canonical mapping $ \widehat {E _ {V} } \rightarrow \widehat{E _ {U} } $ is nuclear.
Let $ E $ be a nuclear space. For any neighbourhood $ U $ of zero in $ E $ and for any $ q $ such that $ 1 \leq q \leq \infty $ there is a convex circled neighbourhood $ V \subset U $ for which $ E _ {V} $ is (norm) isomorphic to a subspace of the space $ l _ {q} $ of sequences with summable $ q $-th powers. Thus, $ E $ coincides with a subspace of the projective limit of a family of spaces isomorphic to $ l _ {q} $. In particular (the case $ q = 2 $), in any nuclear space $ E $ there is a basis of neighbourhoods of zero $ \{ U _ \alpha \} $ such that all the spaces $ \widehat{E _ {U _ \alpha } } $ are Hilbert spaces; thus, $ E $ is Hilbertian, that is, the topology in $ E $ can be generated by a family of semi-norms each of which is obtained from a certain non-negative definite Hermitian form on $ E \times E $. Any complete nuclear space is isomorphic to the projective limit of a family of Hilbert spaces. A space $ E $ of type $ ( {\mathcal F} ) $ is nuclear if and only if it can be represented as the projective limit $ E = \lim\limits _ \leftarrow g _ {mn} H _ {n} $ of a countable family of Hilbert spaces $ H _ {n} $, such that the $ g _ {mn} $ are nuclear operators (or, at least, Hilbert–Schmidt operators, cf. Hilbert–Schmidt operator) for $ m < n $.
Bases in nuclear spaces.
In a nuclear space every equicontinuous basis is absolute. In a space of type $ ( {\mathcal F} ) $ any countable basis (even if weak) is an equicontinuous Schauder basis (cf. Basis), so that in a nuclear space of type $ ( {\mathcal F} ) $ any basis is absolute (in particular, unconditional). A similar result holds for complete nuclear spaces of type $ ( {\mathcal D} {\mathcal F} ) $, and for all nuclear spaces for which the closed-graph theorem holds. A quotient space of a nuclear space of type $ ( {\mathcal F} ) $ with a basis does not necessarily have a basis (see [4], [5], [6]).
Let $ E $ be a nuclear space of type $ ( {\mathcal F} ) $. A topology can be defined in $ E $ by a countable system of semi-norms $ x \mapsto \| x \| _ {q} $, $ q = 1, 2 \dots $ where $ \| x \| _ {q} \leq \| x \| _ {q + 1 } $ for all $ x \in E $. If $ E $ has a basis or a continuous norm, then the semi-norms $ \| \cdot \| $ can be taken as norms. Let $ \{ e _ {n} \} $ be a basis in $ E $; then any $ x \in E $ can be expressed as an (absolutely and unconditionally) convergent series
$$ x = \ \sum _ {n = 1 } ^ \infty \xi _ {n} e _ {n} , $$
where the coordinates $ \xi _ {n} $ have the form $ \xi _ {n} = \langle x, x _ {n} ^ \prime \rangle $, and the functionals $ x _ {n} ^ \prime $ form a bi-orthogonal basis in $ E ^ \prime $. $ E $ is isomorphic to the Köthe space $ {\mathcal K} ( a _ {nq} ) $, where $ a _ {nq} = \| e _ {n} \| _ {q} $; under this isomorphism $ x \in E $ goes into the sequence $ \{ \xi _ {n} \} $ of its coordinates. A basis $ \{ f _ {n} \} $ in $ E $ is equivalent to the basis $ \{ e _ {n} \} $ (that is, it can be obtained from $ \{ e _ {n} \} $ by an isomorphism) if and only if $ {\mathcal K} ( \| e _ {n} \| _ {q} ) $ and $ {\mathcal K} ( \| f _ {n} \| _ {q} ) $ coincide as sets [4]. A basis $ \{ f _ {n} \} $ is called regular (or proper) if there is a system of norms $ \| \cdot \| _ {q} $ and a permutation $ \sigma $ of indices such that $ \| f _ {\sigma ( n) } \| _ {q} / \| f _ {\sigma ( n) } \| _ {r} $ is monotone decreasing for all $ r \geq q $. If a nuclear space $ E $ of type $ ( {\mathcal F} ) $ has a regular basis, then any two bases in $ E $ are quasi-equivalent (that is, they can be made equivalent by a permutation and a normalization of the elements of one of them). There are other sufficient conditions for all bases in $ E $ to be quasi-equivalent (see [4], [14]). A complete description of the class of nuclear spaces with this property is not known (1984).
Example. The Hermite functions $ \phi _ {n} ( t) = e ^ {t ^ {2} /2 } ( {d ^ {n} } / {dt ^ {n} } ) ( e ^ {- t ^ {2} } ) $ form a basis in the complete metric nuclear space $ {\mathcal S} ( \mathbf R ) $ of smooth functions on the real line that are rapidly decreasing together with all their derivatives. $ {\mathcal S} ( \mathbf R ) $ is isomorphic to $ {\mathcal K} ( n ^ {p} ) $.
References
| [1] | A. Grothendieck, "Produits tensoriels topologiques et espaces nucléaires" , Amer. Math. Soc. (1955) |
| [2] | I.M. Gel'fand, N.Ya. Vilenkin, "Generalized functions. Applications of harmonic analysis" , 4 , Acad. Press (1968) (Translated from Russian) |
| [3] | R.A. Minlos, "Generalized random processes and their extension in measure" Trudy Moskov. Mat. Obshch. , 8 (1959) pp. 497–518 (In Russian) |
| [4] | B.S. Mityagin, "Approximate dimension and bases in nuclear spaces" Russian Math. Surveys , 16 : 4 pp. 59–127 Uspekhi Mat. Nauk , 16 : 4 (1961) pp. 63–132 |
| [5] | A. Pietsch, "Nuclear locally convex spaces" , Springer (1972) (Translated from German) |
| [6] | E. Dubinsky, "Structure of nuclear Fréchet spaces" , Springer (1979) |
| [7] | N.M. Zobin, B.S. Mityagin, "Examples of nuclear linear metric spaces without a basis" Funct. Anal. Appl. , 8 : 4 (1974) pp. 304–313 Funktsional. Anal. i Prilozhen. , 8 : 4 (1974) pp. 35–47 |
| [8] | A. Atzmon, "An operator without invariant subspaces on a nuclear Fréchet space" Ann. of Math. , 117 : 3 (1983) pp. 669–694 |
| [9] | H.H. Schaefer, "Topological vector spaces" , Springer (1971) |
| [10] | T. Komura, Y. Komura, "Ueber die Einbettung der nuklearen Räume in 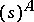 " Math. Ann. , 162 (1965–1966) pp. 284–288 " Math. Ann. , 162 (1965–1966) pp. 284–288 |
| [11] | S. Dineen, "Complex analysis in locally convex spaces" , North-Holland (1981) |
| [12] | K. John, V. Zizler, "On a tensor product characterization of nuclearity" Math. Ann. , 244 : 1 (1979) pp. 83–87 |
| [13] | G. Pisier, "Contre-example à une conjecture de Grothendieck" C.R. Acad. Sci. Paris , 293 (1981) pp. 681–683 (English abstract) |
| [14] | M.M. Dragilev, "Bases in Köthe spaces" , Rostov-on-Don (1983) (In Russian) |
Comments
A generalized function is also called a distribution, and a generalized function of slow growth is also called a tempered distribution.
Let $ F $ be a topological linear space, $ U $ a neighbourhood of zero in $ F $, $ A $ a set in $ F $, and $ \epsilon $ a (small) positive number. An $ \epsilon $-set for $ A $ relative to a neighbourhood $ U $ of zero is a set $ B $ such that for every $ a \in A $ there is a $ b \in B $ such that $ a \in b + \epsilon U $. Let $ N ( \epsilon , A , U ) $ be the smallest number of elements in $ \epsilon $-sets for $ A $ relative to $ U $. The functional dimension of $ F $ is defined by
$$ \mathop{\rm df} ( F ) = \sup _ { U } \inf _ { V } \ {\lim\limits \sup } _ {\epsilon \rightarrow 0 } \ \frac{ { \mathop{\rm ln} \mathop{\rm ln} } N ( \epsilon , V , U ) }{ { \mathop{\rm ln} \mathop{\rm ln} } \epsilon ^ {- 1} } , $$
where $ U , V $ range over the neighbourhoods of zero in $ F $. Cf. [2], Sect. I.3.8 for more details.
Let $ F $ be a locally convex space and consider two neighbourhoods of zero $ U , V $ such that $ U $ absorbs $ V $, i.e. $ V \subset \rho U $ for some positive number $ \rho $. Let
$$ \delta _ {r} ( U , V ) = \inf \{ \delta : \exists \ \textrm{ subspace } G \textrm{ of dimension } \leq r $$
$$ {} \textrm{ such that } V \subset \delta U + G \} . $$
This number is called the $ r $-th diameter of $ V $ with respect to $ U $. The diametral dimension of a locally convex space is the collection of all sequences $ ( d _ {r} ) _ {r \in \mathbf N \cup \{ 0 \} } $ of non-negative numbers with the property that for each neighbourhood of zero $ U $ there is a neighbourhood $ V $ of zero absorbed by $ U $ for which $ \delta _ {r} ( U , V ) \leq d _ {r} $, $ r \in \mathbf N \cup \{ 0 \} $.
A locally convex space $ E $ is nuclear if and only if for some (respectively, each) positive number $ \lambda $ the sequence $ ( ( r + 1 ) ^ {- \lambda } ) _ {r \in N \cup \{ 0 \} } $ belongs to the diametral dimension of $ E $. See [5], Chapt. 9 for more details.
Let again $ U , V $ be neighbourhoods of zero of a locally convex space $ F $ such that $ U $ absorbs $ V $. The $ \epsilon $-content of $ V $ with respect to $ U $ is the supremum $ M _ \epsilon ( U , V ) $ of all natural numbers $ m $ such that there are $ x _ {1} \dots x _ {m} \in V $ with $ x _ {1} \dots x _ {k} \notin \epsilon U $ for all $ i \neq k $. The approximative dimension of a locally convex space $ F $ is the collection of all positive functions $ \phi $ on $ ( 0 , \infty ) $ such that for each neighbourhood $ U $ of zero there is a neighbourhood $ V $ of zero absorbed by $ U $ such that
$$ \lim\limits _ {\epsilon \rightarrow 0 } \phi ( \epsilon ) ^ {- 1} M _ \epsilon ( U , V ) = 0 . $$
The number $ \rho ( U , V ) $ is defined by the exponential rate of growth of $ M _ \epsilon ( U , V ) $ as $ \epsilon \rightarrow 0 $. More precisely,
$$ \rho ( U , V ) = {\lim\limits \sup } _ {\epsilon \rightarrow 0 } \ \frac{ { \mathop{\rm ln} \mathop{\rm ln} } M _ \epsilon ( U , V ) }{ \mathop{\rm ln} \epsilon ^ {- 1} } . $$
A locally convex space $ E $ is nuclear if and only if for some (respectively, each) positive number $ \rho $ the following condition is satisfied: For each neighbourhood of zero $ U $ there is a neighbourhood $ V $ of zero absorbed by $ U $ such that $ \rho ( U , V ) \leq \rho $. Cf. [5], Chapt. 9 for more details.
Let $ U $ be a bounded circled neighbourhood of a topological vector space $ F $. The Minkowski functional associated to $ U $ is defined by
$$ q ( x) = \inf _ {x \in \alpha U } \alpha ,\ \ \alpha \geq 0 . $$
This is well-defined for each $ x $ since $ U $ is absorbent (i.e. for each $ x \in F $ there is an $ \alpha $ such that $ x \in \alpha U $). Cf. [a7], Sects. 15.10, 16.4.
References
| [a1] | A. Grothendieck, "Résumé de la théorie métrique des produits tensoriels topologiques" Bol. Soc. Mat. Sao-Paulo , 8 (1956) pp. 1–79 |
| [a2] | A. Grothendieck, "Topological vector spaces" , Gordon & Breach (1973) (Translated from French) |
| [a3] | H. Jarchow, "Locally convex spaces" , Teubner (1981) (Translated from German) |
| [a4] | G. Pisier, "Factorization of linear operators and geometry of Banach spaces" , Amer. Math. Soc. (1986) |
| [a5] | G. Pisier, "Counterexamples to a conjecture of Grothendieck" Acta. Math. , 151 (1983) pp. 181–208 |
| [a6] | J.F. Colombeau, "Differential calculus and holomorphy" , North-Holland (1982) |
| [a7] | G. Köthe, "Topological vector spaces" , 1 , Springer (1969) |
Nuclear space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nuclear_space&oldid=17938