Moduli problem
The classical problem of the rationality or uni-rationality of the moduli variety of algebraic curves of genus 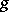 .
.
Riemann surfaces of genus 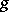 (up to isomorphism) depend on
(up to isomorphism) depend on 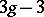 complex parameters — the moduli (see Moduli of a Riemann surface). The set of classes of non-singular projective curves of genus
complex parameters — the moduli (see Moduli of a Riemann surface). The set of classes of non-singular projective curves of genus 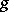 over an algebraically closed field
over an algebraically closed field  has the structure of a quasi-projective algebraic variety
has the structure of a quasi-projective algebraic variety 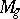 (see [3]–[5]).
(see [3]–[5]).
The manifolds 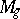 for
for 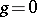 and 1 have a simple structure:
and 1 have a simple structure: 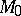 consists of one point, and
consists of one point, and 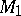 is isomorphic to the affine line
is isomorphic to the affine line 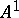 . Therefore the moduli problem refers to curves of genus
. Therefore the moduli problem refers to curves of genus 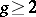 and is formulated as follows: Is the moduli variety
and is formulated as follows: Is the moduli variety 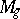 of curves of genus
of curves of genus  rational, or at least uni-rational? The rationality of
rational, or at least uni-rational? The rationality of 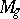 has been established only for
has been established only for 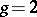 (see [2], where
(see [2], where 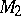 is explicitly described).
is explicitly described).
A general method for proving uni-rationality of 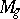 has been constructed [6]. By this method, in particular, the uni-rationality of
has been constructed [6]. By this method, in particular, the uni-rationality of 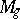 for all
for all 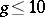 has been proved. The uni-rationality of
has been proved. The uni-rationality of 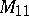 ,
, 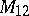 and
and 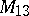 has also been proved.
has also been proved.
The moduli problem frequently receives a broader interpretation (see, for example, [5]): It refers to the whole complex of problems associated with the existence of moduli spaces of certain algebraic objects (varieties, vector bundles, endomorphisms, etc.), with the study of their various algebraic-geometric properties and with compactification techniques for moduli spaces (see Moduli theory).
References
| [1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
| [2] | J. Igusa, "Arithmetic variety of moduli for genus two" Ann. of Math. , 72 : 3 (1960) pp. 612–649 |
| [3] | D. Mumford, "Geometric invariant theory" , Springer (1965) |
| [4] | D. Mumford, "Stability of projective varieties" l'Enseign. Math. (2) , 23 : 1–2 (1977) pp. 39–110 |
| [5] | H. Popp, "Moduli theory and classification theory of algebraic varieties" , Springer (1977) |
| [6] | F. Severi, "Sulla classificazione delle curve algebriche e sul teorema d'esistenza di Riemann" Atti R. Accad. Naz. Lincei Rend. , 24 (1915) pp. 877–888 |
Comments
It is now known that 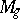 is of general type (cf. General-type algebraic surface) for
is of general type (cf. General-type algebraic surface) for 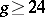 and has positive Kodaira dimension for
and has positive Kodaira dimension for 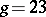 (cf. [a1], [a2]); thus
(cf. [a1], [a2]); thus  is not uni-rational for
is not uni-rational for 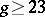 . For
. For 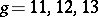 ,
, 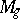 is uni-rational. Also,
is uni-rational. Also, 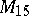 has negative Kodaira dimension. The nature of
has negative Kodaira dimension. The nature of 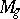 for
for 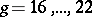 is still (1989) unknown.
is still (1989) unknown.
References
| [a1] | M. Chang, Z. Ran, "Unirationality of the moduli space of curves of genus 11, 13 (and 12)" Invent. Math. , 76 (1984) pp. 41–54 |
| [a2] | D. Eisebud, J. Harris, "The Kodaira dimension of the moduli space of curves of genus 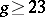 " Invent. Math. , 90 (1987) pp. 359–387 " Invent. Math. , 90 (1987) pp. 359–387 |
| [a3] | J. Harris, D. Mumford, "On the Kodaira dimension of the moduli space of curves" Invent. Math. , 67 (1982) pp. 23–86 |
| [a4] | S. Mori, S. Mukai, "Uniruledness of the moduli space of curves of genus 11" M. Reynard (ed.) T. Shioda (ed.) , Algebraic geometry , Lect. notes in math. , 1016 , Springer (1983) pp. 334–353 |
| [a5] | E. Sernesi, "L'unirazionalità della varietà dei moduli delle curvi di genere dodici" Ann. Scuola Norm. Sup. Pisa (IV) , VIII (1981) pp. 405–439 |
| [a6] | N. Shepherd-Barron, "The rationality of certain spaces associated to trigonal curves" S.J. Bloch (ed.) , Algebraic geometry , Proc. Symp. Pure Math. , 46.1 , Amer. Math. Soc. (1987) pp. 165–171 |
| [a7] | N. Shepherd-Barron, "Invariant theory for 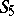 and the rationality of and the rationality of 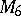 " Compos. Math. , 70 (1989) pp. 13–25 " Compos. Math. , 70 (1989) pp. 13–25 |
| [a8] | J. Harris, "Curves and their moduli" S.J. Bloch (ed.) , Algebraic geometry , Proc. Symp. Pure Math. , 46.1 , Amer. Math. Soc. (1985) pp. 99–143 |
| [a9] | D. Eisenbud, J. Harris, "Limit linear series" Bull. Amer. Math. Soc. , 10 (1984) pp. 277–280 |
Moduli problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Moduli_problem&oldid=15845