Minimal model

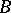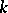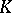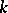An algebraic variety which is minimal relative to the existence of birational morphisms into non-singular varieties. More precisely, let be the class of all birationally-equivalent non-singular varieties over an algebraically closed field , the fields of functions of which are isomorphic to a given finitely-generated extension over . The varieties in the class 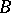are called projective models of this class, or projective models of the field 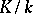. A variety 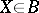is called a relatively minimal model if every birational morphism 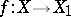, where 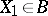, is an isomorphism. In other words, a relatively minimal model is a minimal element in 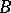with respect to the partial order defined by the following domination relation: 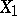dominates 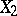if there exists a birational morphism 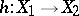. If a relatively minimal model is unique in 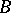, then it is called the minimal model.

In each class of birationally-equivalent curves there is a unique (up to an isomorphism) non-singular projective curve. So each non-singular projective curve is a minimal model. In the general case, if 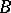is not empty, then it contains at least one relatively minimal model. The non-emptiness of 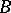is known (thanks to theorems about resolution of singularities) for varieties of arbitrary dimension in characteristic 0 for and for varieties of dimension 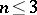in characteristic .

The basic results on minimal models of algebraic surfaces are included in the following.

1) A non-singular projective surface 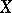is a relatively minimal model if and only if it does not contain exceptional curves of the first kind (see Exceptional subvariety).

2) Every non-singular complete surface has a birational morphism onto a relatively minimal model.

3) In each non-empty class 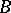of birationally-equivalent surfaces, except for the classes of rational and ruled surfaces, there is a (moreover, unique) minimal model.

4) If 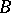is the class of ruled surfaces (cf. Ruled surface) with a curve 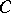of genus 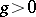as base, then all relatively minimal models in are exhausted by the geometric ruled surfaces .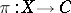

5) If 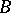is the class of rational surfaces, then all relatively minimal models in 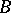are exhausted by the projective plane 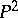and the series of minimal rational ruled surfaces 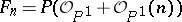for all integers 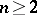and .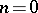

There is (see [6], [7]) a generalization of the theory of minimal models of surfaces to regular two-dimensional schemes. Minimal models of rational surfaces over an arbitrary field have been described (see [2]).

References

[1]	I.R. Shafarevich, "Algebraic surfaces" Proc. Steklov Inst. Math. , 75 (1975) Trudy Mat. Inst. Steklov. , 75 (1975)
[2]	V.A. Iskovskikh, "Minimal models of rational surfaces over arbitrary fields" Math. USSR Izv. , 14 : 1 (1980) pp. 17–39 Izv. Akad. Nauk SSSR Ser. Mat. , 43 : 1 (1979) pp. 19–43
[3]	I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian)
[4]	D. Husemoller, "Classification and embeddings of surfaces" R. Hartshorne (ed.) , Algebraic geometry (Arcata, 1974) , Proc. Symp. Pure Math. , 29 , Amer. Math. Soc. (1975) pp. 329–420
[5]	R. Hartshorne, "Algebraic geometry" , Springer (1977)
[6]	S. Lichtenbaum, "Curves over discrete valuation rings" Amer. J. Math. , 90 : 2 (1968) pp. 380–405
[7]	I.R. Shafarevich, "Lectures on minimal models and birational transformations of two-dimensional schemes" , Tata Inst. (1966)

Comments

Since 1982 important progress has been made (over the field of complex numbers) in the theory of minimal models for higher-dimensional varieties, and especially for varieties of dimension 3. It has turned out to be necessary to allow a mild type of singularities, namely so-called terminal and canonical singularities. For the precise (very technical) definitions see the references below. (Terminal singularities are special canonical singularities, and for surfaces a point with a terminal (respectively, canonical) singularity is in fact smooth (respectively, a rational double point).) Allowing terminal singularities, the "minimal model problemminimal model problem" (i.e. the existence of a minimal model in a class of birational equivalence) has been solved by S. Mori for varieties of dimension three; in particular, for non-uniruled -dimensional algebraic varieties [a2]. A new phenomenon in the higher-dimensional case is also the non-uniqueness of minimal models. References [a1], [a2] and [a4] are good surveys of this new theory.

References

[a1]	J. Kollár, "The structure of algebraic threefolds: an introduction to Mori's program" Bull. Amer. Math. Soc. , 17 (1987) pp. 211–273
[a2]	S. Mori, "Flip theorem and the existence of minimal models for 3-folds" J. Amer. Math. Soc. , 1 (1988) pp. 117–253
[a3]	S. Mori, "Classification of higher-dimensional varieties" , Algebraic geometry , Proc. Symp. Pure Math. , 46, Part 1 , Amer. Math. Soc. (1987) pp. 165–171
[a4]	P.M.H. Wilson, "Toward a birational classification of algebraic varieties" Bull. London Math. Soc. , 19 (1987) pp. 1–48
[a5]	J. Kollár, "Minimal models of algebraic threefolds: Mori's program" Sém. Bourbaki , 712 (1989)
[a6]	Y. Kawamata, K. Matsuda, K. Matsuki, "Introduction to the minimal model problem" T. Oda (ed.) , Algebraic geometry (Sendai, 1985) , North-Holland & Kinokuniya (1987) pp. 283–360