Meijer-G-functions
Generalizations of the hypergeometric functions 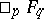 of one variable (cf. also Hypergeometric function). They can be defined by an integral as
of one variable (cf. also Hypergeometric function). They can be defined by an integral as
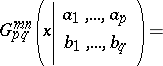 |
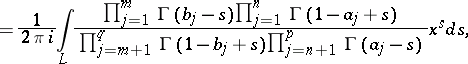 |
where  ,
, 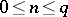 and the parameters
and the parameters 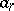 ,
, 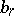 are such that no pole of the functions
are such that no pole of the functions 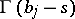 coincides with any pole of the functions
coincides with any pole of the functions 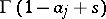 . There are three possible choices for the contour
. There are three possible choices for the contour 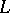 :
:
a) 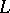 goes from
goes from 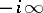 to
to  remaining to the right of the poles of
remaining to the right of the poles of 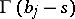 and to the left of the poles of
and to the left of the poles of 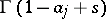 ;
;
b) 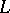 begins and ends at
begins and ends at 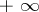 , encircles counterclockwise all poles of
, encircles counterclockwise all poles of 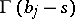 and does not encircle any pole of
and does not encircle any pole of 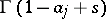 ;
;
c) 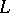 begins and ends at
begins and ends at 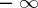 , encircles clockwise all poles of
, encircles clockwise all poles of 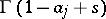 and does not encircle any pole of
and does not encircle any pole of 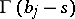 .
.
The integral converges if 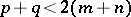 ,
, 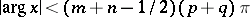 in case a); if
in case a); if 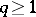 and either
and either 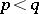 or
or  and
and  in case b); and if
in case b); and if 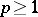 and either
and either 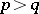 or
or  and
and 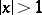 in case c).
in case c).
The integral defining the Meijer 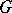 -functions can be calculated by means of the residue theorem and one obtains expressions for
-functions can be calculated by means of the residue theorem and one obtains expressions for 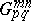 in terms of the hypergeometric functions
in terms of the hypergeometric functions 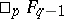 or
or 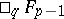 . The function
. The function 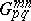 satisfies the linear differential equation
satisfies the linear differential equation
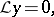 |
where
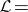 |
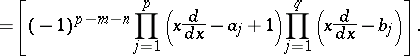 |
Many functions of hypergeometric type and their products can be expressed in terms of Meijer 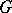 -functions, [a1]. For example,
-functions, [a1]. For example,
 |
 |
Meijer  -functions appear in the theory of Lie group representations (cf. also Representation of a compact group) as transition coefficients for different bases of carrier spaces of representations [a2].
-functions appear in the theory of Lie group representations (cf. also Representation of a compact group) as transition coefficients for different bases of carrier spaces of representations [a2].
References
| [a1] | A. Erdelyi, W. Magnus, F. Oberhettinger, F. Tricomi, "Higher transcendental functions" , 1 , McGraw-Hill (1953) |
| [a2] | N.J. Vilenkin, A.U. Klimyk, "Representation of Lie groups and special functions" , 2 , Kluwer Acad. Publ. (1993) (In Russian) |
Meijer-G-functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Meijer-G-functions&oldid=13688