L'Hospital rule
l'Hôpital's rule
A rule for removing indeterminacies of the form 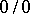 or
or 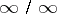 by reducing the limit of the ratio of functions to the limit of the ratio of the derivatives of the functions in question. Thus, for the case when the real-valued functions
by reducing the limit of the ratio of functions to the limit of the ratio of the derivatives of the functions in question. Thus, for the case when the real-valued functions 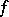 and
and 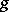 are defined in a punctured right neighbourhood of a point
are defined in a punctured right neighbourhood of a point  on the number axis, l'Hospital's rule has the form
on the number axis, l'Hospital's rule has the form
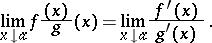 | (*) |
Both in the case of an indeterminacy of the form 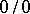 , that is, when
, that is, when
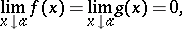 |
and in the case 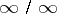 , that is, when
, that is, when
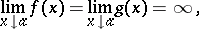 |
l'Hospital's rule is valid under the conditions that 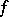 and
and 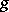 are differentiable on some interval
are differentiable on some interval 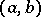 ,
, 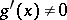 for all points
for all points 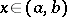 , and that there is a finite or infinite limit of the ratio of the derivatives:
, and that there is a finite or infinite limit of the ratio of the derivatives:
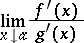 |
(in the case of an indeterminacy of the form 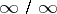 , this limit, if it is infinite, can only be an infinity of definite sign); then the limit of the ratio of the functions
, this limit, if it is infinite, can only be an infinity of definite sign); then the limit of the ratio of the functions 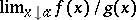 exists and (*) holds. This assertion remains true, with natural changes, for the case of a left-sided and also a two-sided limit, and also when
exists and (*) holds. This assertion remains true, with natural changes, for the case of a left-sided and also a two-sided limit, and also when 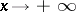 or
or 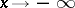 .
.
In a practical search for limits of ratios of functions by means of l'Hospital's rule one must sometimes apply it several times in succession.
Under the assumptions made above, the existence of a limit of the ratio of derivatives 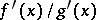 is a sufficient condition for the existence of a limit of the ratio
is a sufficient condition for the existence of a limit of the ratio 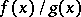 of the functions themselves, but it is not necessary.
of the functions themselves, but it is not necessary.
References
| [1] | G.F. l'Hospital, "Analyse des infiniment petits pour l'intellligence des lignes courbes" , Paris (1696) |
| [2] | S.M. Nikol'skii, "A course of mathematical analysis" , 1 , MIR (1977) (Translated from Russian) |
Comments
The "rule" is probably due to Johann Bernoulli, who taught the marquis de l'Hospital mathematics.
References
| [a1] | G.E. Shilov, "Mathematical analysis" , 1–2 , M.I.T. (1974) (Translated from Russian) |
| [a2] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1976) pp. 107–108 |
| [a3] | K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) |
L'Hospital rule. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=L%27Hospital_rule&oldid=14236