Inverse hyperbolic functions

Functions inverse to the hyperbolic functions. The inverse hyperbolic functions are the inverse hyperbolic sine, cosine and tangent: 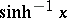, , 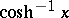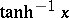; other notations are: , , .

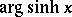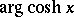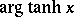The inverse hyperbolic functions of a real variable are defined by the formulas

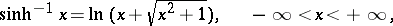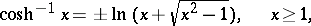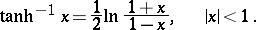The inverse hyperbolic functions are single-valued and continuous at each point of their domain of definition, except for 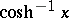, which is two-valued. In studying the properties of the inverse hyperbolic functions, one of the continuous branches of 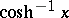is chosen, that is, in the formula above only one sign is taken (usually plus). For the graphs of these functions see the figure.

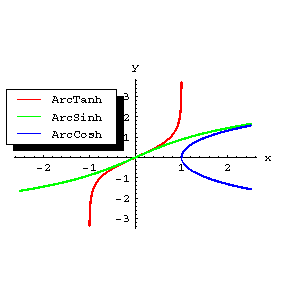
Figure: i052370a

There a number of relations between the inverse hyperbolic functions. For example,

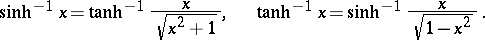The derivatives of the inverse hyperbolic functions are given by the formulas

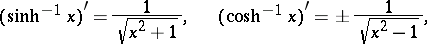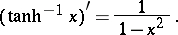The inverse hyperbolic functions of a complex variable are defined by the same formulas as those for a real variable , where 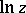is understood to be the many-valued logarithmic function. The inverse hyperbolic functions of a complex variable are the analytic continuations to the complex plane of the corresponding functions of a real variable.

The inverse hyperbolic functions can be expressed in terms of the inverse trigonometric functions by the formulas

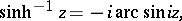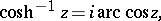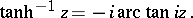Comments

The notations 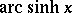, 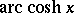and 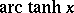are also quite common.

References

[a1]	M.R. Spiegel, "Complex variables" , Schaum's Outline Series , McGraw-Hill (1974)
[a2]	M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1972)