Difference between revisions of "Hedetniemi conjecture"
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| − | For two graphs | + | {{TEX|done}} |
| + | For two graphs $A$ and $B$ (cf. [[Graph|Graph]]), their categorial product $A\times B$ is the graph with vertex set $V(A\times B)=V(A)\times V(B)$ while an edge $(a_0,b_0)$ is adjacent to an edge $(a_1,b_1)$ if and only if $a_0$ is adjacent to $a_1$ and $b_0$ is adjacent to $b_1$. If the graph $A$ has a good $n$-colouring $\gamma$ (cf. [[Graph colouring|Graph colouring]]), then $A\times B$ has a good $n$-colouring $\gamma^*$, given by $\gamma^*(a,b)=\gamma(a)$. As this statement also holds for good $n$-colourings of $B$, it follows that the chromatic number $\chi(A\times B)\leq\min\{\chi(A),\chi(B)\}$. Hedetniemi's conjecture, [[#References|[a1]]], is that for all finite graphs $A$ and $B$: | ||
| − | + | $$\chi(A\times B)=\min\{\chi(A),\chi(B)\}.$$ | |
| − | The corresponding statement for infinite graphs is not true [[#References|[a2]]], but little is known about the relationship between the cardinalities of the chromatic numbers of | + | The corresponding statement for infinite graphs is not true [[#References|[a2]]], but little is known about the relationship between the cardinalities of the chromatic numbers of $A$ and $B$ and the chromatic number of $A\times B$. |
| − | It is obvious that the chromatic number of the product of two | + | It is obvious that the chromatic number of the product of two $2$-chromatic graphs is $2$. L. Lovász [[#References|[a3]]] showed that the chromatic number of the product of two $3$-chromatic graphs is $3$ and in [[#References|[a4]]] it is proven that the chromatic number of the product of two $4$-chromatic graphs is $4$. It is not known whether the chromatic number of the product of two $n$-chromatic graphs is always $n$ for any $n\geq5$. The lack of understanding of this problem is even more embarrassing than that. |
| − | Let | + | Let $f(n)$ be the largest number such that whenever $A$ and $B$ are two $n$-chromatic graphs, then the chromatic number of $A\times B$ is larger than or equal to $f(n)$. Clearly, if $n\geq4$, then $4\leq f(n)\leq n$ and Hedetniemi's conjecture says that $f(n)=n$. About $f(n)$ it is only known that either $f(n)\leq9$ for all $n$ or $f(n)$ is unbounded, [[#References|[a5]]] and [[#References|[a6]]]. |
| − | Write | + | Write $A\mapsto B$ if there is a homomorphism from the graph $A$ to the graph $B$ (a function from $A$ to $B$ which preserves the edges). Write $A\not\mapsto B$ if there is no homomorphism from $A$ to $B$. A graph $M$ is called multiplicative, [[#References|[a7]]], [[#References|[a8]]], if $A\not\mapsto M$ and $B\not\mapsto M$ imply $A\times B\not\mapsto M$. Note that a graph $A$ has a good $n$-colouring if and only if $A\mapsto K_n$. Hence Hedetniemi's conjecture is equivalent to asking whether the complete graph $K_n$ (cf. also [[Graph|Graph]]) is multiplicative. |
| − | Two graphs | + | Two graphs $A$ and $B$ are equivalent, $A\sim B$, if $A\mapsto B$ and $B\mapsto A$. It is not difficult to check that the equivalence classes of finite graphs form a [[Distributive lattice|distributive lattice]] under the order relation $\mapsto$ and that a graph is multiplicative if and only if it is meet-irreducible in this lattice. Once this general setting of the problem has been realized, it is not difficult to see that Hedetniemi's conjecture has a natural generalization, [[#References|[a8]]], to the problem of finding the meet-irreducible elements in the distributive lattices of various types of relational structures. This line of investigation leads to a setting in [[Topos|topos]] theory and, to a certain extent, in logic, [[#References|[a9]]]. |
Of course this introduces the even more general task of trying to understand the distributive lattice of, say, all finite relational structures of a given type and, in connection with this, the problem of deciding whether there is a homomorphism from a given relational structure to another one of the same type. In this context one of the more interesting types of relational structures are finite directed graphs, [[#References|[a10]]]. Multiplicative partially ordered sets have been investigated in [[#References|[a11]]]. | Of course this introduces the even more general task of trying to understand the distributive lattice of, say, all finite relational structures of a given type and, in connection with this, the problem of deciding whether there is a homomorphism from a given relational structure to another one of the same type. In this context one of the more interesting types of relational structures are finite directed graphs, [[#References|[a10]]]. Multiplicative partially ordered sets have been investigated in [[#References|[a11]]]. | ||
| Line 18: | Line 19: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S. Hedetniemi, "Homomorphisms of graphs and automata" ''Univ. Michigan Technical Report'' , '''03105–44–T''' (1966)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Hajnal, "The chromatic number of the product of two | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S. Hedetniemi, "Homomorphisms of graphs and automata" ''Univ. Michigan Technical Report'' , '''03105–44–T''' (1966)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Hajnal, "The chromatic number of the product of two $KAPAJA_1$-chromatic graphs can be countable" ''Combinatorica'' , '''5''' (1985) pp. 137–140</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> L. Lovász, "Operations with structures" ''Acta Math. Acad. Sci. Hung.'' (1967) pp. 321–328</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M.H. El-Zahar, N.W. Sauer, "The chromatic number of the product of two <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110110/h11011072.png" />-chromatic graphs is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110110/h11011073.png" />" ''Combinatorica'' , '''5''' : 2 (1985) pp. 121–126</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> S. Poljak, "Coloring digraphs by iterated antichains" ''Comment. Math. Univ. Carolin.'' , '''32''' : 2 (1991) pp. 209–212</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> S. Poljak, V. Rödl, "On the arc-chromatic number of a digraph" ''JCT B'' , '''31''' (1981) pp. 190–198</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> D.J. Miller, "The categorical product of graphs" ''Canad. J. Math.'' , '''20''' (1968) pp. 1511–1521</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> R. Haggkvist, P. Hell, D.J. Miller, V.N. Lara, "On multiplicative graphs and the product conjecture" ''Combinatorica'' , '''8''' : 1 (1988) pp. 63–74</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> D. Duffus, N.W. Sauer, "Lattices arising in categorial investigations of Hedetniemi's conjecture" ''Discrete Math.'' , '''153''' (1996)</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> P. Hell, H. Zhou, X. Zhu, "Homomorphisms to oriented cycles" ''Combinatorica'' (??)</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> N.W. Sauer, X. Zhu, "Multiplicative posets" ''Order'' , '''8''' (1992) pp. 349–358</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> D. Duffus, B. Sands, R. Woodrow, "On the chromatic number of the product of graphs" ''J. Graph Th.'' , '''9''' (1985) pp. 487–495</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> N.W. Sauer, X. Zhu, "An approach to Hedetniemi's conjecture" ''J. Graph Th.'' , '''16''' : 5 (1992) pp. 423–436</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> G. Sabidussi, "Graph multiplication" ''Math. Z.'' , '''72''' (1960) pp. 446–457</TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> R.J. Nowakowski, D. Rall, "Associative graph products and their independence, domination and coloring numbers" ''J. Graph Th.'' (??)</TD></TR></table> |
Revision as of 15:24, 22 September 2014
For two graphs $A$ and $B$ (cf. Graph), their categorial product $A\times B$ is the graph with vertex set $V(A\times B)=V(A)\times V(B)$ while an edge $(a_0,b_0)$ is adjacent to an edge $(a_1,b_1)$ if and only if $a_0$ is adjacent to $a_1$ and $b_0$ is adjacent to $b_1$. If the graph $A$ has a good $n$-colouring $\gamma$ (cf. Graph colouring), then $A\times B$ has a good $n$-colouring $\gamma^*$, given by $\gamma^*(a,b)=\gamma(a)$. As this statement also holds for good $n$-colourings of $B$, it follows that the chromatic number $\chi(A\times B)\leq\min\{\chi(A),\chi(B)\}$. Hedetniemi's conjecture, [a1], is that for all finite graphs $A$ and $B$:
$$\chi(A\times B)=\min\{\chi(A),\chi(B)\}.$$
The corresponding statement for infinite graphs is not true [a2], but little is known about the relationship between the cardinalities of the chromatic numbers of $A$ and $B$ and the chromatic number of $A\times B$.
It is obvious that the chromatic number of the product of two $2$-chromatic graphs is $2$. L. Lovász [a3] showed that the chromatic number of the product of two $3$-chromatic graphs is $3$ and in [a4] it is proven that the chromatic number of the product of two $4$-chromatic graphs is $4$. It is not known whether the chromatic number of the product of two $n$-chromatic graphs is always $n$ for any $n\geq5$. The lack of understanding of this problem is even more embarrassing than that.
Let $f(n)$ be the largest number such that whenever $A$ and $B$ are two $n$-chromatic graphs, then the chromatic number of $A\times B$ is larger than or equal to $f(n)$. Clearly, if $n\geq4$, then $4\leq f(n)\leq n$ and Hedetniemi's conjecture says that $f(n)=n$. About $f(n)$ it is only known that either $f(n)\leq9$ for all $n$ or $f(n)$ is unbounded, [a5] and [a6].
Write $A\mapsto B$ if there is a homomorphism from the graph $A$ to the graph $B$ (a function from $A$ to $B$ which preserves the edges). Write $A\not\mapsto B$ if there is no homomorphism from $A$ to $B$. A graph $M$ is called multiplicative, [a7], [a8], if $A\not\mapsto M$ and $B\not\mapsto M$ imply $A\times B\not\mapsto M$. Note that a graph $A$ has a good $n$-colouring if and only if $A\mapsto K_n$. Hence Hedetniemi's conjecture is equivalent to asking whether the complete graph $K_n$ (cf. also Graph) is multiplicative.
Two graphs $A$ and $B$ are equivalent, $A\sim B$, if $A\mapsto B$ and $B\mapsto A$. It is not difficult to check that the equivalence classes of finite graphs form a distributive lattice under the order relation $\mapsto$ and that a graph is multiplicative if and only if it is meet-irreducible in this lattice. Once this general setting of the problem has been realized, it is not difficult to see that Hedetniemi's conjecture has a natural generalization, [a8], to the problem of finding the meet-irreducible elements in the distributive lattices of various types of relational structures. This line of investigation leads to a setting in topos theory and, to a certain extent, in logic, [a9].
Of course this introduces the even more general task of trying to understand the distributive lattice of, say, all finite relational structures of a given type and, in connection with this, the problem of deciding whether there is a homomorphism from a given relational structure to another one of the same type. In this context one of the more interesting types of relational structures are finite directed graphs, [a10]. Multiplicative partially ordered sets have been investigated in [a11].
For graphs, Hedetniemi's conjecture has been confirmed for various special cases and several interesting observations have been made. See [a12], [a13], [a14]. For a general discussion of graph products, see [a15].
References
| [a1] | S. Hedetniemi, "Homomorphisms of graphs and automata" Univ. Michigan Technical Report , 03105–44–T (1966) |
| [a2] | A. Hajnal, "The chromatic number of the product of two $KAPAJA_1$-chromatic graphs can be countable" Combinatorica , 5 (1985) pp. 137–140 |
| [a3] | L. Lovász, "Operations with structures" Acta Math. Acad. Sci. Hung. (1967) pp. 321–328 |
| [a4] | M.H. El-Zahar, N.W. Sauer, "The chromatic number of the product of two 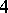 -chromatic graphs is -chromatic graphs is  " Combinatorica , 5 : 2 (1985) pp. 121–126 " Combinatorica , 5 : 2 (1985) pp. 121–126 |
| [a5] | S. Poljak, "Coloring digraphs by iterated antichains" Comment. Math. Univ. Carolin. , 32 : 2 (1991) pp. 209–212 |
| [a6] | S. Poljak, V. Rödl, "On the arc-chromatic number of a digraph" JCT B , 31 (1981) pp. 190–198 |
| [a7] | D.J. Miller, "The categorical product of graphs" Canad. J. Math. , 20 (1968) pp. 1511–1521 |
| [a8] | R. Haggkvist, P. Hell, D.J. Miller, V.N. Lara, "On multiplicative graphs and the product conjecture" Combinatorica , 8 : 1 (1988) pp. 63–74 |
| [a9] | D. Duffus, N.W. Sauer, "Lattices arising in categorial investigations of Hedetniemi's conjecture" Discrete Math. , 153 (1996) |
| [a10] | P. Hell, H. Zhou, X. Zhu, "Homomorphisms to oriented cycles" Combinatorica (??) |
| [a11] | N.W. Sauer, X. Zhu, "Multiplicative posets" Order , 8 (1992) pp. 349–358 |
| [a12] | D. Duffus, B. Sands, R. Woodrow, "On the chromatic number of the product of graphs" J. Graph Th. , 9 (1985) pp. 487–495 |
| [a13] | N.W. Sauer, X. Zhu, "An approach to Hedetniemi's conjecture" J. Graph Th. , 16 : 5 (1992) pp. 423–436 |
| [a14] | G. Sabidussi, "Graph multiplication" Math. Z. , 72 (1960) pp. 446–457 |
| [a15] | R.J. Nowakowski, D. Rall, "Associative graph products and their independence, domination and coloring numbers" J. Graph Th. (??) |
Hedetniemi conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hedetniemi_conjecture&oldid=13925