Difference between revisions of "Hecke operator"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 65 formulas out of 67 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 67 formulas, 65 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|partial}} | |
| + | Let $M ( k )$ be the vector space of (entire) modular forms of weight $k$, see [[Modular form|Modular form]] or [[#References|[a1]]]. Then the Hecke operator $T _ { n }$ is defined for $f \in M ( k )$ by | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h130/h130060/h1300605.png"/></td> <td style="width:5%;text-align:right;" valign="top">(a1)</td></tr></table> | |
| − | + | where $\tau \in H$, the upper half-plane. One (easily) proves that $T _ { n } f \in M ( k )$ if $f \in M ( k )$. | |
| + | |||
| + | If $f ( z ) = \sum _ { m = 0 } ^ { \infty } c ( m ) q ^ { m } ( z )$, $q ( z ) = e ^ { 2 \pi i z }$, is the Fourier expansion of $f$, then | ||
| + | |||
| + | \begin{equation*} T _ { n } f ( z ) = \sum _ { m = 0 } ^ { \infty } \gamma _ { n } ( m ) q ^ { m } ( z ), \end{equation*} | ||
with | with | ||
| − | + | \begin{equation*} \gamma _ { n } ( m ) = \sum _ { d | ( n , m ) } d ^ { k - 1 } c \left( \frac { m n } { d ^ { 2 } } \right). \end{equation*} | |
Note that | Note that | ||
| − | + | \begin{equation*} T _ { n } T _ { m } = \sum _ { d | ( n , m ) } d ^ { k - 1 } T _ { m n / d^2 } , \end{equation*} | |
| − | so that, in particular, the | + | so that, in particular, the $T _ { n }$ commute. |
The discriminant form | The discriminant form | ||
| − | + | \begin{equation*} \Delta ( z ) = ( 2 \pi ) ^ { 12 } \sum _ { m = 1 } ^ { \infty } \tau ( m ) q ^ { m } ( z ) \in M ( 12 ), \end{equation*} | |
| − | where | + | where $\tau ( m )$ is the Ramanujan function, is a simultaneous eigenfunction of all $T _ { n }$. |
| − | Formula (a1) can be regarded as coming from an operation on lattices in the complex plane, | + | Formula (a1) can be regarded as coming from an operation on lattices in the complex plane, $\widetilde{T} _ { n } ( L ) = \sum L ^ { \prime }$, where the sum is over all sublattices of $L$ of index $n$. This geometric definition, [[#References|[a4]]], makes (a1) easier to understand. |
| − | There are Hecke operators in much more general settings, e.g. for suitable subgroups of the [[Modular group|modular group]] | + | There are Hecke operators in much more general settings, e.g. for suitable subgroups of the [[Modular group|modular group]] $\Gamma$. A quite abstract group setting follows, [[#References|[a6]]]. |
| − | Let | + | Let $G$ be a [[Group|group]] and $D$ a subgroup. Another subgroup $D ^ { \prime }$ is commensurable with $D$ if $D \cap D ^ { \prime }$ is of finite index in both $D$ and $D ^ { \prime }$. Let $\widetilde { D } = \{ \alpha \in G : \alpha D \alpha ^ { - 1 } \text { is commensurable with} \ D\}$. This is a subgroup of $G$ that contains $D$. |
| − | Now, let | + | Now, let $R$ be the $\bf Z$-module of all formal sums $\sum c _ { \alpha } D \alpha D$, i.e. the free Abelian group on the double cosets of $D$ in $\widetilde { D }$. There is an associative multiplication on $R$, defined as follows. Let $u = D \alpha D$, $v = D \beta D$. Then the product $u v = D \alpha D \beta D$ is clearly a (disjoint) union of double cosets. It gives a product $u . v$, provided multiplicities are taken into account. More precisely, let $D \alpha D = \coprod _ { \alpha ^ { \prime } \in A } D \alpha ^ { \prime }$, $D \beta D = \coprod _ { \beta ^ { \prime } \in A } D \beta ^ { \prime }$. Then |
| − | + | \begin{equation*} ( D \alpha D ) ( D \beta D ) = D \alpha D \beta D = D \alpha ( \bigcup _ { \beta ^ { \prime } } D \beta ^ { \prime } ) = \end{equation*} | |
| − | + | \begin{equation*} = \bigcup _ { \beta ^ { \prime } } D \alpha D \beta ^ { \prime } = \bigcup _ { \alpha ^ { \prime } , \beta ^ { \prime } } D \alpha ^ { \prime } \beta ^ { \prime }. \end{equation*} | |
| − | Now, let | + | Now, let $\mu ( u \cdot v , w ) = \# \{ ( \alpha ^ { \prime } , \beta ^ { \prime } ) \in A \times B : D \alpha ^ { \prime } \beta ^ { \prime } = D \xi \,\text { with } w = D \xi D \}$. Then $u\cdot v = \sum _ { w } \mu ( u \cdot v , w ) w$. (The restriction of the $D \alpha D$ to $\alpha \in \widetilde{ D }$ is needed to keep things, e.g. the sets $A$, $B$, finite.) |
| − | Let | + | Let $X$ be a subset of $\widetilde { D }$ containing $D$ and multiplicatively closed. Then one defines $R _ { 0 } ( X , D )$ as the submodule of $R$ spanned by the $D \xi D$ for $\xi \in X$. This gives a subring of $R$. Finally, one defines $R ( X , D )$, the Hecke algebra of $( X , D )$ as $R_0 ( X , D ) \otimes \mathbf{Q}$. |
| − | In many situations the double cosets | + | In many situations the double cosets $D \xi D$ act on forms, functions, etc., which gives Hecke operators. See [[#References|[a5]]] for an example in the case of double cosets with respect to the principal congruence subgroup |
| − | + | \begin{equation*} \Gamma ( n ) = \end{equation*} | |
| − | + | \begin{equation*} = \left\{ \left( \begin{array} { l l } { a } & { b } \\ { c } & { d } \end{array} \right) \in \operatorname{SL} ( 2 , \mathbf{Z} ) : \left( \begin{array} { c c } { a } & { b } \\ { c } & { d } \end{array} \right) \equiv \left( \begin{array} { l l } { 1 } & { 0 } \\ { 0 } & { 1 } \end{array} \right) ( \operatorname { mod } n ) \right\}, \end{equation*} | |
which gives rise to the (usual) Hecke operators for modular forms. | which gives rise to the (usual) Hecke operators for modular forms. | ||
| Line 54: | Line 62: | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> T.M. Apostol, "Modular functions and Dirichlet series in number theory" , Springer (1976) pp. 120ff</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> N. Hurt, "Quantum chaos and mesoscopic systems" , Kluwer Acad. Publ. (1997) pp. 101; 163ff</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> M.I. Knopp, "Modular functions in analytic number theory" , Markham Publ. (1970)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> A. Ogg, "Modular forms and Dirichlet series" , Benjamin (1969) pp. Chap. II</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> R.A. Rankin, "Modular forms and functions" , Cambridge Univ. Press (1977) pp. Chap. 9</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> G. Shimura, "Euler products and Eisenstein series" , Amer. Math. Soc. (1997) pp. Sect. 11</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> A.B. Venkov, "Spectral theory of automorphic functions" , Kluwer Acad. Publ. (1990) pp. 34; 59</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> D. Bump, "Automorphic forms and representations" , Cambridge Univ. Press (1997)</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> N.E. Hurt, "Exponential sums and coding theory. A review" ''Acta Applic. Math.'' , '''46''' (1997) pp. 49–91</td></tr></table> |
Revision as of 16:55, 1 July 2020
Let $M ( k )$ be the vector space of (entire) modular forms of weight $k$, see Modular form or [a1]. Then the Hecke operator $T _ { n }$ is defined for $f \in M ( k )$ by
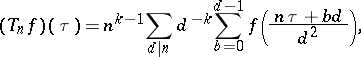 | (a1) |
where $\tau \in H$, the upper half-plane. One (easily) proves that $T _ { n } f \in M ( k )$ if $f \in M ( k )$.
If $f ( z ) = \sum _ { m = 0 } ^ { \infty } c ( m ) q ^ { m } ( z )$, $q ( z ) = e ^ { 2 \pi i z }$, is the Fourier expansion of $f$, then
\begin{equation*} T _ { n } f ( z ) = \sum _ { m = 0 } ^ { \infty } \gamma _ { n } ( m ) q ^ { m } ( z ), \end{equation*}
with
\begin{equation*} \gamma _ { n } ( m ) = \sum _ { d | ( n , m ) } d ^ { k - 1 } c \left( \frac { m n } { d ^ { 2 } } \right). \end{equation*}
Note that
\begin{equation*} T _ { n } T _ { m } = \sum _ { d | ( n , m ) } d ^ { k - 1 } T _ { m n / d^2 } , \end{equation*}
so that, in particular, the $T _ { n }$ commute.
The discriminant form
\begin{equation*} \Delta ( z ) = ( 2 \pi ) ^ { 12 } \sum _ { m = 1 } ^ { \infty } \tau ( m ) q ^ { m } ( z ) \in M ( 12 ), \end{equation*}
where $\tau ( m )$ is the Ramanujan function, is a simultaneous eigenfunction of all $T _ { n }$.
Formula (a1) can be regarded as coming from an operation on lattices in the complex plane, $\widetilde{T} _ { n } ( L ) = \sum L ^ { \prime }$, where the sum is over all sublattices of $L$ of index $n$. This geometric definition, [a4], makes (a1) easier to understand.
There are Hecke operators in much more general settings, e.g. for suitable subgroups of the modular group $\Gamma$. A quite abstract group setting follows, [a6].
Let $G$ be a group and $D$ a subgroup. Another subgroup $D ^ { \prime }$ is commensurable with $D$ if $D \cap D ^ { \prime }$ is of finite index in both $D$ and $D ^ { \prime }$. Let $\widetilde { D } = \{ \alpha \in G : \alpha D \alpha ^ { - 1 } \text { is commensurable with} \ D\}$. This is a subgroup of $G$ that contains $D$.
Now, let $R$ be the $\bf Z$-module of all formal sums $\sum c _ { \alpha } D \alpha D$, i.e. the free Abelian group on the double cosets of $D$ in $\widetilde { D }$. There is an associative multiplication on $R$, defined as follows. Let $u = D \alpha D$, $v = D \beta D$. Then the product $u v = D \alpha D \beta D$ is clearly a (disjoint) union of double cosets. It gives a product $u . v$, provided multiplicities are taken into account. More precisely, let $D \alpha D = \coprod _ { \alpha ^ { \prime } \in A } D \alpha ^ { \prime }$, $D \beta D = \coprod _ { \beta ^ { \prime } \in A } D \beta ^ { \prime }$. Then
\begin{equation*} ( D \alpha D ) ( D \beta D ) = D \alpha D \beta D = D \alpha ( \bigcup _ { \beta ^ { \prime } } D \beta ^ { \prime } ) = \end{equation*}
\begin{equation*} = \bigcup _ { \beta ^ { \prime } } D \alpha D \beta ^ { \prime } = \bigcup _ { \alpha ^ { \prime } , \beta ^ { \prime } } D \alpha ^ { \prime } \beta ^ { \prime }. \end{equation*}
Now, let $\mu ( u \cdot v , w ) = \# \{ ( \alpha ^ { \prime } , \beta ^ { \prime } ) \in A \times B : D \alpha ^ { \prime } \beta ^ { \prime } = D \xi \,\text { with } w = D \xi D \}$. Then $u\cdot v = \sum _ { w } \mu ( u \cdot v , w ) w$. (The restriction of the $D \alpha D$ to $\alpha \in \widetilde{ D }$ is needed to keep things, e.g. the sets $A$, $B$, finite.)
Let $X$ be a subset of $\widetilde { D }$ containing $D$ and multiplicatively closed. Then one defines $R _ { 0 } ( X , D )$ as the submodule of $R$ spanned by the $D \xi D$ for $\xi \in X$. This gives a subring of $R$. Finally, one defines $R ( X , D )$, the Hecke algebra of $( X , D )$ as $R_0 ( X , D ) \otimes \mathbf{Q}$.
In many situations the double cosets $D \xi D$ act on forms, functions, etc., which gives Hecke operators. See [a5] for an example in the case of double cosets with respect to the principal congruence subgroup
\begin{equation*} \Gamma ( n ) = \end{equation*}
\begin{equation*} = \left\{ \left( \begin{array} { l l } { a } & { b } \\ { c } & { d } \end{array} \right) \in \operatorname{SL} ( 2 , \mathbf{Z} ) : \left( \begin{array} { c c } { a } & { b } \\ { c } & { d } \end{array} \right) \equiv \left( \begin{array} { l l } { 1 } & { 0 } \\ { 0 } & { 1 } \end{array} \right) ( \operatorname { mod } n ) \right\}, \end{equation*}
which gives rise to the (usual) Hecke operators for modular forms.
In [a6] this setting is used to define Hecke operators for the case of adelic groups.
Modular forms turn up all over mathematics and physics and, hence, so do the Hecke operators. See the references for a variety of uses of them.
References
| [a1] | T.M. Apostol, "Modular functions and Dirichlet series in number theory" , Springer (1976) pp. 120ff |
| [a2] | N. Hurt, "Quantum chaos and mesoscopic systems" , Kluwer Acad. Publ. (1997) pp. 101; 163ff |
| [a3] | M.I. Knopp, "Modular functions in analytic number theory" , Markham Publ. (1970) |
| [a4] | A. Ogg, "Modular forms and Dirichlet series" , Benjamin (1969) pp. Chap. II |
| [a5] | R.A. Rankin, "Modular forms and functions" , Cambridge Univ. Press (1977) pp. Chap. 9 |
| [a6] | G. Shimura, "Euler products and Eisenstein series" , Amer. Math. Soc. (1997) pp. Sect. 11 |
| [a7] | A.B. Venkov, "Spectral theory of automorphic functions" , Kluwer Acad. Publ. (1990) pp. 34; 59 |
| [a8] | D. Bump, "Automorphic forms and representations" , Cambridge Univ. Press (1997) |
| [a9] | N.E. Hurt, "Exponential sums and coding theory. A review" Acta Applic. Math. , 46 (1997) pp. 49–91 |
Hecke operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hecke_operator&oldid=13264