Hardy-Ramanujan theorem
(on the normal number of prime factors of an integer)
For any integer  , let
, let 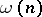 denote the number of distinct prime factors of
denote the number of distinct prime factors of  . The Hardy–Ramanujan theorem [a5] states that the function
. The Hardy–Ramanujan theorem [a5] states that the function 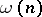 has normal order
has normal order 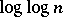 in the sense that, given any
in the sense that, given any 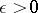 , almost all positive integers
, almost all positive integers  satisfy
satisfy
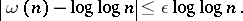 |
Here, "almost all" means that the number of positive integers 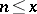 for which the indicated property holds is asymptotically equal to
for which the indicated property holds is asymptotically equal to  as
as 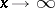 . A stronger, and best-possible, version of this result shows that, given any real-valued function
. A stronger, and best-possible, version of this result shows that, given any real-valued function 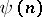 tending to infinity as
tending to infinity as 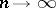 , almost all positive integers
, almost all positive integers  satisfy
satisfy
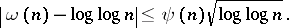 |
The same estimate holds for the function 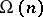 , the total number of prime factors of
, the total number of prime factors of  , i.e., the number of prime factors of
, i.e., the number of prime factors of  counted with multiplicity.
counted with multiplicity.
The Hardy–Ramanujan theorem led to the development of probabilistic number theory, a branch of number theory in which properties of integers are studied from a probabilistic point of view (see [a1] or [a6] for a general reference and also Number theory, probabilistic methods in). One of the main theorems in this area, and a far-reaching generalization of the Hardy–Ramanujan theorem, is the Erdös–Kac theorem, which states that the functions 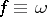 and
and 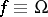 (and, in fact, a large class of additive functions
(and, in fact, a large class of additive functions 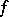 ; cf. Additive arithmetic function) satisfy
; cf. Additive arithmetic function) satisfy
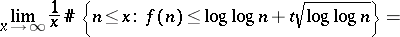 |
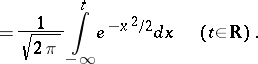 |
This shows that the values of 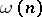 and
and 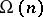 are, in a sense, normally distributed with mean
are, in a sense, normally distributed with mean 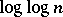 and standard deviation
and standard deviation 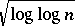 (cf. also Normal distribution).
(cf. also Normal distribution).
Another generalization of the Hardy–Ramanujan theorem, due to P. Erdös ([a2]; see also [a4], Chapt. 1), describes the size of the prime factors of a random integer. For 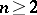 , let
, let 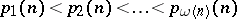 denote the sequence of distinct prime factors of
denote the sequence of distinct prime factors of  . Let
. Let 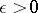 be given, and let
be given, and let 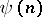 be a function tending arbitrarily slowly to infinity as
be a function tending arbitrarily slowly to infinity as 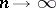 . Then, for almost-all positive integers
. Then, for almost-all positive integers  , the inequalities
, the inequalities
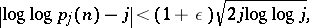 |
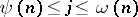 |
hold. A related result, due to J. Galambos [a3], is that the numbers 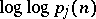 are, in a suitable sense, normally distributed with mean
are, in a suitable sense, normally distributed with mean 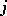 and standard deviation
and standard deviation 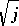 ; see [a3].
; see [a3].
References
| [a1] | P.D.T.A. Elliott, "Probabilistic number theory" , I–II , Springer (1979-1980) |
| [a2] | P. Erdös, "On the distribution function of additive functions" Ann. of Math. , 47 (1946) pp. 1–20 |
| [a3] | J. Galambos, "The sequences of prime divisors of integers" Acta Arith. , 31 (1976) pp. 213–218 |
| [a4] | R.R. Hall, G. Tenenbaum, "Divisors" , Tracts in Math. , 90 , Cambridge Univ. Press (1988) |
| [a5] | G.H. Hardy, S. Ramanujan, "The normal number of prime factors of a number  " Quart. J. Math. , 48 (1917) pp. 76–92 " Quart. J. Math. , 48 (1917) pp. 76–92 |
| [a6] | G. Tenenbaum, "Introduction to analytic and probabilistic number theory" , Cambridge Univ. Press (1995) |
Hardy-Ramanujan theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hardy-Ramanujan_theorem&oldid=13663