Haken manifold
sufficiently-large  -manifold, sufficiently-large three-dimensional manifold
-manifold, sufficiently-large three-dimensional manifold
A compact, 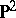 -irreducible three-dimensional manifold which contains a properly embedded, incompressible, two-sided surface.
-irreducible three-dimensional manifold which contains a properly embedded, incompressible, two-sided surface.
All objects and mappings are in the piecewise-linear category (cf. also Piecewise-linear topology). The surface 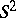 denotes the two-dimensional sphere, while
denotes the two-dimensional sphere, while 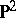 denotes the projective plane. A surface
denotes the projective plane. A surface 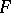 properly embedded in a three-dimensional manifold
properly embedded in a three-dimensional manifold 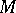 is two-sided in
is two-sided in 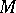 if it separates its regular neighbourhood in
if it separates its regular neighbourhood in 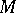 . A three-dimensional manifold
. A three-dimensional manifold 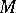 is reducible (reducible with respect to connected sum decomposition) if it contains a properly embedded two-dimensional sphere that does not bound a three-dimensional cell in
is reducible (reducible with respect to connected sum decomposition) if it contains a properly embedded two-dimensional sphere that does not bound a three-dimensional cell in  . Otherwise, the three-dimensional manifold
. Otherwise, the three-dimensional manifold 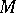 is irreducible. If the three-dimensional manifold
is irreducible. If the three-dimensional manifold 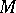 is irreducible and does not contain an embedded, two-sided
is irreducible and does not contain an embedded, two-sided 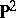 , it is said to be
, it is said to be 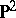 -irreducible. An orientable three-dimensional manifold is
-irreducible. An orientable three-dimensional manifold is 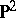 -irreducible if it is irreducible. A surface
-irreducible if it is irreducible. A surface 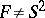 which is properly embedded in a three-dimensional manifold
which is properly embedded in a three-dimensional manifold 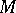 is compressible in
is compressible in 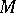 if there is a disc
if there is a disc 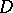 embedded in
embedded in 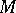 such that
such that 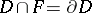 and the simple closed curve
and the simple closed curve 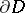 does not bound a disc in
does not bound a disc in 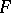 . Otherwise, such a surface
. Otherwise, such a surface 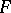 is said to be incompressible in
is said to be incompressible in 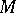 . For two-sided surfaces it follows from the Dehn lemma that this geometric condition is equivalent to the inclusion mapping of fundamental groups,
. For two-sided surfaces it follows from the Dehn lemma that this geometric condition is equivalent to the inclusion mapping of fundamental groups, 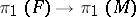 , being injective.
, being injective.
The three-dimensional cell is a Haken manifold, as is any compact, 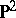 -irreducible three-dimensional manifold with non-empty boundary. In fact, a sufficient condition for a compact,
-irreducible three-dimensional manifold with non-empty boundary. In fact, a sufficient condition for a compact, 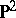 -irreducible three-dimensional manifold
-irreducible three-dimensional manifold 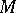 to be a Haken manifold is that its first homology group with rational coefficients,
to be a Haken manifold is that its first homology group with rational coefficients, 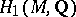 , be non-zero. This condition is not necessary. Any closed three-dimensional manifold which is not a Haken manifold is said to be a non-Haken manifold. It is conjectured that every closed,
, be non-zero. This condition is not necessary. Any closed three-dimensional manifold which is not a Haken manifold is said to be a non-Haken manifold. It is conjectured that every closed, 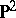 -irreducible three-dimensional manifold with infinite fundamental group has a finite sheeted covering space (cf. also Covering surface) that is a Haken manifold.
-irreducible three-dimensional manifold with infinite fundamental group has a finite sheeted covering space (cf. also Covering surface) that is a Haken manifold.
An embedded, incompressible surface in a three-dimensional manifold is a very useful tool. However, in the case of three-dimensional manifolds with non-empty boundary, it is necessary to add an additional condition related to the boundary to achieve the same geometric character of the incompressible surface in a closed three-dimensional manifold. A properly embedded surface 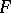 in a three-dimensional manifold
in a three-dimensional manifold 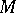 with non-empty boundary is boundary compressible, written
with non-empty boundary is boundary compressible, written 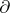 -compressible, if there is a disc
-compressible, if there is a disc 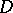 embedded in
embedded in 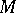 such that
such that 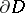 is the union of two arcs
is the union of two arcs 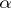 and
and 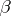 ,
, 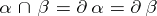 ,
, 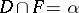 ,
, 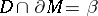 , and
, and  does not cobound a disc in
does not cobound a disc in 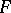 with an arc in
with an arc in  . If a properly embedded surface
. If a properly embedded surface  in a three-dimensional manifold
in a three-dimensional manifold 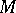 is not
is not 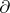 -compressible, it is said to be boundary incompressible (
-compressible, it is said to be boundary incompressible (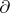 -incompressible). There is an algebraic interpretation of this geometric condition in terms of relative fundamental groups analogous to that given above in the case of an incompressible surface. Any compact,
-incompressible). There is an algebraic interpretation of this geometric condition in terms of relative fundamental groups analogous to that given above in the case of an incompressible surface. Any compact, 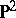 -irreducible three-dimensional manifold
-irreducible three-dimensional manifold 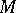 with non-empty boundary, other than the three-dimensional cell, contains a properly embedded, incompressible and
with non-empty boundary, other than the three-dimensional cell, contains a properly embedded, incompressible and 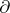 -incompressible surface that is not a disc parallel into
-incompressible surface that is not a disc parallel into 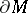 .
.
Just as two-dimensional manifolds have families of embedded simple closed curves that split them into more simple pieces, the existence of incompressible and 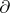 -incompressible surfaces in Haken manifolds allow them to be split into more simple pieces. If
-incompressible surfaces in Haken manifolds allow them to be split into more simple pieces. If 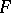 is a properly embedded, two-sided surface in a three-dimensional manifold
is a properly embedded, two-sided surface in a three-dimensional manifold 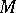 and
and 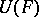 is the interior of some regular neighbourhood of
is the interior of some regular neighbourhood of 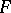 in
in 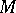 , then
, then 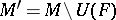 is the three-dimensional manifold obtained by splitting
is the three-dimensional manifold obtained by splitting 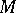 at
at 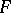 . A partial hierarchy for
. A partial hierarchy for 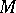 is a finite or infinite sequence of manifold pairs
is a finite or infinite sequence of manifold pairs
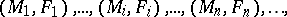 |
where 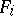 is a properly embedded, two-sided, incompressible surface in
is a properly embedded, two-sided, incompressible surface in 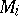 which is not parallel into the boundary of
which is not parallel into the boundary of 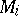 , and
, and 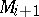 is obtained from
is obtained from 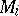 by splitting
by splitting 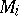 at
at  . A partial hierarchy is said to be a hierarchy for
. A partial hierarchy is said to be a hierarchy for 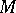 if for some
if for some  , each component of
, each component of 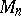 is a a three-dimensional cell. Necessarily, a hierarchy for
is a a three-dimensional cell. Necessarily, a hierarchy for 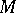 is a finite partial hierarchy,
is a finite partial hierarchy, 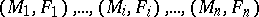 , and
, and  is called the length of the hierarchy.
is called the length of the hierarchy.
The fundamental theorem for Haken manifolds is that every Haken manifold has a hierarchy, 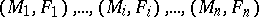 , where each
, where each 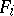 is incompressible and
is incompressible and 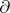 -incompressible in
-incompressible in 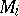 . The existence of a hierarchy admits inductive methods of analysis and proof. This is exhibited in many of the major results regarding three-dimensional manifolds. For example, the problem of determining if two given three-dimensional manifolds are homeomorphic (the homeomorphism problem), the problem of determining if a given loop in a three-dimensional manifold is contractible (the word problem), and the problem of determining if a closed, orientable, irreducible, atoroidal (having no embedded, incompressible tori) three-dimensional manifold admits a metric with constant negative curvature, (uniformization), have all been solved for Haken manifolds but remain open (as of 2000) for closed, orientable, irreducible three-dimensional manifolds in general. The study of Haken manifolds is quite rich and includes a large part of the knowledge and understanding of three-dimensional manifolds.
. The existence of a hierarchy admits inductive methods of analysis and proof. This is exhibited in many of the major results regarding three-dimensional manifolds. For example, the problem of determining if two given three-dimensional manifolds are homeomorphic (the homeomorphism problem), the problem of determining if a given loop in a three-dimensional manifold is contractible (the word problem), and the problem of determining if a closed, orientable, irreducible, atoroidal (having no embedded, incompressible tori) three-dimensional manifold admits a metric with constant negative curvature, (uniformization), have all been solved for Haken manifolds but remain open (as of 2000) for closed, orientable, irreducible three-dimensional manifolds in general. The study of Haken manifolds is quite rich and includes a large part of the knowledge and understanding of three-dimensional manifolds.
References
| [a1] | W. Haken, "Theorie der Normal Flächen I" Acta Math. , 105 (1961) pp. 245–375 |
| [a2] | F. Waldhausen, "On irreducible  -manifolds which are sufficiently large" Ann. of Math. , 87 (1968) pp. 56–88 -manifolds which are sufficiently large" Ann. of Math. , 87 (1968) pp. 56–88 |
| [a3] | W. Thurston, "Three-dimensional manifolds, Kleinian groups and hyperbolic geometry" Bull. Amer. Math. Soc. (N.S.) , 6 (1982) pp. 357–381 |
| [a4] | F. Waldhausen, "The word problem in fundamental groups of sufficiently large irreducible 3-manifolds" Ann. of Math. , 88 (1968) pp. 272–280 |
| [a5] | A.T. Fomenko, S.V. Matveev, "Algorithmic and computer methods for three-manifolds" , Kluwer Acad. Publ. (1997) |
Haken manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Haken_manifold&oldid=12727