Fredholm theorems
for integral equations
Theorem 1.
The homogeneous equation
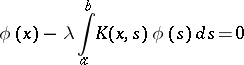 | (1) |
and its transposed equation
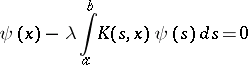 | (2) |
have, for a fixed value of the parameter 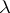 , either only the trivial solution, or have the same finite number of linearly independent solutions:
, either only the trivial solution, or have the same finite number of linearly independent solutions: 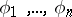 ;
;  .
.
Theorem 2.
For a solution of the inhomogeneous equation
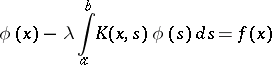 | (3) |
to exist it is necessary and sufficient that its right-hand side be orthogonal to a complete system of linearly independent solutions of the corresponding homogeneous transposed equation (2):
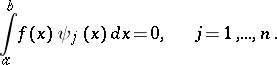 | (4) |
Theorem 3.
(the Fredholm alternative). Either the inhomogeneous equation (3) has a solution, whatever its right-hand side 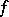 , or the corresponding homogeneous equation (1) has non-trivial solutions.
, or the corresponding homogeneous equation (1) has non-trivial solutions.
Theorem 4.
The set of characteristic numbers of equation (1) is at most countable, with a single possible limit point at infinity.
For the Fredholm theorems to hold in the function space 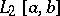 it is sufficient that the kernel
it is sufficient that the kernel 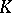 of equation (3) be square-integrable on the set
of equation (3) be square-integrable on the set 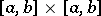 (
( and
and 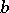 may be infinite). When this condition is violated, (3) may turn out to be a non-Fredholm integral equation. When the parameter
may be infinite). When this condition is violated, (3) may turn out to be a non-Fredholm integral equation. When the parameter 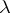 and the functions involved in (3) take complex values, then instead of the transposed equation (2) one often considers the adjoint equation to (1):
and the functions involved in (3) take complex values, then instead of the transposed equation (2) one often considers the adjoint equation to (1):
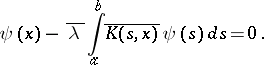 |
In this case condition (4) is replaced by
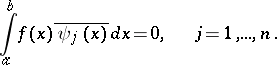 |
These theorems were proved by E.I. Fredholm [1].
References
| [1] | E.I. Fredholm, "Sur une classe d'equations fonctionnelles" Acta Math. , 27 (1903) pp. 365–390 |
Comments
Instead of the phrases "transposed equation" and "adjoint equation" one sometimes uses "adjoint equation of a Fredholm integral equationadjoint equation" and "conjugate equation of a Fredholm integral equationconjugate equation" (cf. [a4]); in the latter terminology 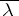 is replaced by
is replaced by 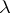 .
.
References
| [a1] | I.C. Gohberg, S. Goldberg, "Basic operator theory" , Birkhäuser (1981) |
| [a2] | K. Jörgens, "Lineare Integraloperatoren" , Teubner (1970) |
| [a3] | V.I. Smirnov, "A course of higher mathematics" , 4 , Addison-Wesley (1964) (Translated from Russian) |
| [a4] | P.P. Zabreiko (ed.) A.I. Koshelev (ed.) M.A. Krasnoselskii (ed.) S.G. Mikhlin (ed.) L.S. Rakovshchik (ed.) V.Ya. Stet'senko (ed.) T.O. Shaposhnikova (ed.) R.S. Anderssen (ed.) , Integral equations - a reference text , Noordhoff (1975) (Translated from Russian) |
Fredholm theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fredholm_theorems&oldid=12814