Difference between revisions of "Equivariant cohomology"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | e0360902.png | ||
| + | $#A+1 = 30 n = 3 | ||
| + | $#C+1 = 30 : ~/encyclopedia/old_files/data/E036/E.0306090 Equivariant cohomology | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A [[Cohomology|cohomology]] that takes the action of some group into account. More precisely, an equivariant cohomology in the category of $ G $- | |
| + | spaces (that is, topological spaces on which the continuous action of a group $ G $ | ||
| + | is defined) and equivariant mappings is a sequence of contravariant functors $ H _ {G} ^ {n} $( | ||
| + | taking values in the category of Abelian groups) and natural transformations | ||
| − | + | $$ | |
| + | H _ {G} ^ {n} ( L) \rightarrow H _ {G} ^ {n+} 1 ( K , L ) ,\ \ | ||
| + | L \subseteq K , | ||
| + | $$ | ||
| + | |||
| + | with the following properties: a) equivariantly-homotopic mappings of pairs induce identity homomorphisms of the groups $ H _ {G} ^ {n} $; | ||
| + | b) an inclusion of the form | ||
| + | |||
| + | $$ | ||
| + | ( K , K \cap L ) \subseteq ( K \cup L , L ) | ||
| + | $$ | ||
induces an isomorphism | induces an isomorphism | ||
| − | + | $$ | |
| + | H _ {G} ^ {n} ( K \cup L , L ) \cong \ | ||
| + | H _ {G} ^ {n} ( K , K \cap L ) ; | ||
| + | $$ | ||
| − | and c) for every pair | + | and c) for every pair $ ( K , L ) $ |
| + | the following cohomology sequence is exact: | ||
| − | + | $$ | |
| + | {} \dots \rightarrow H _ {G} ^ {n} ( K , L ) \rightarrow H _ {G} ^ {n} ( K) \rightarrow \ | ||
| + | H _ {G} ^ {n} ( L) \rightarrow H _ {G} ^ {n+} 1 ( K , L ) \rightarrow \dots . | ||
| + | $$ | ||
| − | Let | + | Let $ \pi : E _ {G} \rightarrow B _ {G} $ |
| + | be a universal [[G-fibration| $ G $- | ||
| + | fibration]] and let $ K _ {G} $ | ||
| + | be the space associated with the universal fibre space $ \pi $ | ||
| + | with fibre $ K $( | ||
| + | that is, the quotient space $ E _ {G} \times K $ | ||
| + | under the action of $ G $ | ||
| + | given by $ g ( l , k ) = ( l g ^ {-} 1 , g k ) $). | ||
| + | Then the functors $ H _ {G} ^ {n} ( K) = H ^ {n} ( K _ {G} ) $ | ||
| + | yield an equivariant cohomology theory; here $ H ^ {n} $ | ||
| + | is an arbitrary cohomology theory. | ||
| − | For any fixed group | + | For any fixed group $ G $ |
| + | the collection of groups $ H _ {G} ^ {n} ( G / F ) $ | ||
| + | together with all possible homomorphisms induced by inclusions $ F _ {1} \subseteq F _ {2} $ | ||
| + | of subgroups of $ G $ | ||
| + | is usually called the system of coefficients for the $ H _ {G} ^ {*} $- | ||
| + | theory. In some cases the functors $ H _ {G} ^ {n} $ | ||
| + | are uniquely defined by their systems of coefficients (for example, when $ G $ | ||
| + | is finite and $ H _ {G} ^ {n} ( G / F ) = 0 $ | ||
| + | for $ n > 0 $). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> G.E. Bredon, "Equivariant cohomology theories" , Springer (1967)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> W.Y. Hsiang, "Cohomology theory of topological transformation groups" , Springer (1975)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> G.E. Bredon, "Equivariant cohomology theories" , Springer (1967)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> W.Y. Hsiang, "Cohomology theory of topological transformation groups" , Springer (1975)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
The principal use of equivariant cohomology is in equivariant obstruction theory and in such problems of equivariant (stable) homotopy theory as the solution of the Segal conjecture by G. Carlsson [[#References|[a1]]] (see also [[#References|[a2]]] and [[Homotopy|Homotopy]]). | The principal use of equivariant cohomology is in equivariant obstruction theory and in such problems of equivariant (stable) homotopy theory as the solution of the Segal conjecture by G. Carlsson [[#References|[a1]]] (see also [[#References|[a2]]] and [[Homotopy|Homotopy]]). | ||
| − | Quite generally, in many parts of mathematics it is useful to consider also family and equivariant versions of various constructions and results. The various family (relative) and equivariant versions of parts of mathematics are then often also important tools in the non-equivariant and non-family settings. An example of this is the use of equivariant | + | Quite generally, in many parts of mathematics it is useful to consider also family and equivariant versions of various constructions and results. The various family (relative) and equivariant versions of parts of mathematics are then often also important tools in the non-equivariant and non-family settings. An example of this is the use of equivariant $ K $- |
| + | theory in proofs of the Atiyah–Singer index and fixed-points theorems, cf., e.g., [[#References|[a3]]]. | ||
| − | Thus, many theories, e.g. cohomology theories, have equivariant versions, e.g. equivariant (stable) homotopy theory [[#References|[a1]]], equivariant | + | Thus, many theories, e.g. cohomology theories, have equivariant versions, e.g. equivariant (stable) homotopy theory [[#References|[a1]]], equivariant $ K $- |
| + | theory [[#References|[a3]]], [[#References|[a4]]], equivariant cobordism [[#References|[a5]]], [[#References|[a7]]]. And there are equivariant versions of many theorems and constructions such as equivariant surgery [[#References|[a1]]], [[#References|[a7]]], equivariant smoothing [[#References|[a6]]] and equivariant transversality [[#References|[a7]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G. Carlsson, "Equivariant stable homotopy and Segal's Burnside ring conjecture" ''Ann. of Math.'' , '''120''' (1984) pp. 189–224</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L.G. Lewis, J.P. May, M. Steinberger, "Equivariant stable homotopy theory" , ''Lect. notes in math.'' , '''1213''' , Springer (1986) (With contributions by J.E. McClure)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> T. Petrie, J.D. Randall, "Transformation groups on manifolds" , M. Dekker (1984)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> T. tom Dieck, "Transformation groups and representation theory" , Springer (1979)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> T. Petrie, "Pseudoequivalences of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e036/e036090/e03609034.png" />-manifolds" R.J. Milgram (ed.) , ''Algebraic and geometric topology'' , '''33.1''' , Amer. Math. Soc. (1978) pp. 169–210</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> R. Lashof, M. Rothenberg, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e036/e036090/e03609035.png" />-smoothing theory" R.J. Milgram (ed.) , ''Algebraic and geometric topology'' , '''33.1''' , Amer. Math. Soc. (1978) pp. 211–266</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> W. Browder, F. Quinn, "A surgery theory for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e036/e036090/e03609036.png" />-manifolds and stratified sets" , ''Manifolds (Tokyo)'' , Univ. Tokyo Press (1973) pp. 27–36</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G. Carlsson, "Equivariant stable homotopy and Segal's Burnside ring conjecture" ''Ann. of Math.'' , '''120''' (1984) pp. 189–224</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L.G. Lewis, J.P. May, M. Steinberger, "Equivariant stable homotopy theory" , ''Lect. notes in math.'' , '''1213''' , Springer (1986) (With contributions by J.E. McClure)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> T. Petrie, J.D. Randall, "Transformation groups on manifolds" , M. Dekker (1984)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> T. tom Dieck, "Transformation groups and representation theory" , Springer (1979)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> T. Petrie, "Pseudoequivalences of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e036/e036090/e03609034.png" />-manifolds" R.J. Milgram (ed.) , ''Algebraic and geometric topology'' , '''33.1''' , Amer. Math. Soc. (1978) pp. 169–210</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> R. Lashof, M. Rothenberg, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e036/e036090/e03609035.png" />-smoothing theory" R.J. Milgram (ed.) , ''Algebraic and geometric topology'' , '''33.1''' , Amer. Math. Soc. (1978) pp. 211–266</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> W. Browder, F. Quinn, "A surgery theory for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e036/e036090/e03609036.png" />-manifolds and stratified sets" , ''Manifolds (Tokyo)'' , Univ. Tokyo Press (1973) pp. 27–36</TD></TR></table> | ||
Revision as of 19:37, 5 June 2020
A cohomology that takes the action of some group into account. More precisely, an equivariant cohomology in the category of $ G $-
spaces (that is, topological spaces on which the continuous action of a group $ G $
is defined) and equivariant mappings is a sequence of contravariant functors $ H _ {G} ^ {n} $(
taking values in the category of Abelian groups) and natural transformations
$$ H _ {G} ^ {n} ( L) \rightarrow H _ {G} ^ {n+} 1 ( K , L ) ,\ \ L \subseteq K , $$
with the following properties: a) equivariantly-homotopic mappings of pairs induce identity homomorphisms of the groups $ H _ {G} ^ {n} $; b) an inclusion of the form
$$ ( K , K \cap L ) \subseteq ( K \cup L , L ) $$
induces an isomorphism
$$ H _ {G} ^ {n} ( K \cup L , L ) \cong \ H _ {G} ^ {n} ( K , K \cap L ) ; $$
and c) for every pair $ ( K , L ) $ the following cohomology sequence is exact:
$$ {} \dots \rightarrow H _ {G} ^ {n} ( K , L ) \rightarrow H _ {G} ^ {n} ( K) \rightarrow \ H _ {G} ^ {n} ( L) \rightarrow H _ {G} ^ {n+} 1 ( K , L ) \rightarrow \dots . $$
Let $ \pi : E _ {G} \rightarrow B _ {G} $ be a universal $ G $- fibration and let $ K _ {G} $ be the space associated with the universal fibre space $ \pi $ with fibre $ K $( that is, the quotient space $ E _ {G} \times K $ under the action of $ G $ given by $ g ( l , k ) = ( l g ^ {-} 1 , g k ) $). Then the functors $ H _ {G} ^ {n} ( K) = H ^ {n} ( K _ {G} ) $ yield an equivariant cohomology theory; here $ H ^ {n} $ is an arbitrary cohomology theory.
For any fixed group $ G $ the collection of groups $ H _ {G} ^ {n} ( G / F ) $ together with all possible homomorphisms induced by inclusions $ F _ {1} \subseteq F _ {2} $ of subgroups of $ G $ is usually called the system of coefficients for the $ H _ {G} ^ {*} $- theory. In some cases the functors $ H _ {G} ^ {n} $ are uniquely defined by their systems of coefficients (for example, when $ G $ is finite and $ H _ {G} ^ {n} ( G / F ) = 0 $ for $ n > 0 $).
References
| [1] | G.E. Bredon, "Equivariant cohomology theories" , Springer (1967) |
| [2] | W.Y. Hsiang, "Cohomology theory of topological transformation groups" , Springer (1975) |
Comments
The principal use of equivariant cohomology is in equivariant obstruction theory and in such problems of equivariant (stable) homotopy theory as the solution of the Segal conjecture by G. Carlsson [a1] (see also [a2] and Homotopy).
Quite generally, in many parts of mathematics it is useful to consider also family and equivariant versions of various constructions and results. The various family (relative) and equivariant versions of parts of mathematics are then often also important tools in the non-equivariant and non-family settings. An example of this is the use of equivariant $ K $- theory in proofs of the Atiyah–Singer index and fixed-points theorems, cf., e.g., [a3].
Thus, many theories, e.g. cohomology theories, have equivariant versions, e.g. equivariant (stable) homotopy theory [a1], equivariant $ K $- theory [a3], [a4], equivariant cobordism [a5], [a7]. And there are equivariant versions of many theorems and constructions such as equivariant surgery [a1], [a7], equivariant smoothing [a6] and equivariant transversality [a7].
References
| [a1] | G. Carlsson, "Equivariant stable homotopy and Segal's Burnside ring conjecture" Ann. of Math. , 120 (1984) pp. 189–224 |
| [a2] | L.G. Lewis, J.P. May, M. Steinberger, "Equivariant stable homotopy theory" , Lect. notes in math. , 1213 , Springer (1986) (With contributions by J.E. McClure) |
| [a3] | T. Petrie, J.D. Randall, "Transformation groups on manifolds" , M. Dekker (1984) |
| [a4] | T. tom Dieck, "Transformation groups and representation theory" , Springer (1979) |
| [a5] | T. Petrie, "Pseudoequivalences of 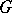 -manifolds" R.J. Milgram (ed.) , Algebraic and geometric topology , 33.1 , Amer. Math. Soc. (1978) pp. 169–210 -manifolds" R.J. Milgram (ed.) , Algebraic and geometric topology , 33.1 , Amer. Math. Soc. (1978) pp. 169–210 |
| [a6] | R. Lashof, M. Rothenberg, "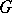 -smoothing theory" R.J. Milgram (ed.) , Algebraic and geometric topology , 33.1 , Amer. Math. Soc. (1978) pp. 211–266 -smoothing theory" R.J. Milgram (ed.) , Algebraic and geometric topology , 33.1 , Amer. Math. Soc. (1978) pp. 211–266 |
| [a7] | W. Browder, F. Quinn, "A surgery theory for 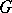 -manifolds and stratified sets" , Manifolds (Tokyo) , Univ. Tokyo Press (1973) pp. 27–36 -manifolds and stratified sets" , Manifolds (Tokyo) , Univ. Tokyo Press (1973) pp. 27–36 |
Equivariant cohomology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Equivariant_cohomology&oldid=18258