Difference between revisions of "De Finetti theorem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | d1100201.png | ||
| + | $#A+1 = 102 n = 2 | ||
| + | $#C+1 = 102 : ~/encyclopedia/old_files/data/D110/D.1100020 De Finetti theorem | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | The following question may be asked: Are the convex combinations of laws of independent identically-distributed random variables the only exchangeable probability measures? The answer is no if < | + | {{TEX|auto}} |
| + | {{TEX|done}} | ||
| + | |||
| + | Consider a sequence of $ N $ | ||
| + | independent identically-distributed random variables $ ( X _ {j} ) $, | ||
| + | $ j = 1 \dots N $, | ||
| + | with $ N \leq \infty $( | ||
| + | cf. [[Random variable|Random variable]]). Clearly, their law is invariant under permutation, i.e. for any finite subset $ F $ | ||
| + | of $ \{ 1 \dots N \} $ | ||
| + | and for any permutation $ \pi $ | ||
| + | of $ F $, | ||
| + | the [[Joint distribution|joint distribution]] of $ ( X _ {\pi ( j ) } ) $( | ||
| + | $ j \in F $) | ||
| + | is the same as the joint distribution of $ ( X _ {j} ) $( | ||
| + | $ j \in F $). | ||
| + | Denoting by $ P $ | ||
| + | the joint law of the $ ( X _ {j} ) $' | ||
| + | s, one can express the above-stated invariance property as follows: $ P \circ \pi = P $. | ||
| + | Clearly, this property of $ P $ | ||
| + | is preserved under convex combinations. A sequence of random variables (or, equivalently, their [[Probability distribution|probability distribution]]) whose finite-dimensional joint laws are invariant under permutations is called exchangeable or symmetric. | ||
| + | |||
| + | The following question may be asked: Are the convex combinations of laws of independent identically-distributed random variables the only exchangeable probability measures? The answer is no if $ N < \infty $, | ||
| + | and yes if $ N = \infty $. | ||
| + | The latter statement is De Finetti's theorem. Thus, an equivalent statement of De Finetti's theorem is that the extremal points of the convex set of exchangeable probability measures on an infinite product space are the laws of sequences of independent identically-distributed random variables. | ||
De Finetti's theorem asserts, moreover, that this convex set is a [[Simplex|simplex]], i.e. any of its points is the barycentre of a unique [[Probability measure|probability measure]], called the mixing measure, concentrated on the extremal points. This statement remains true for probability measures that are invariant under groups much more general than the (finite) permutations on the natural integers, while the product structure of the extremals seems to be specific to the permutation group. | De Finetti's theorem asserts, moreover, that this convex set is a [[Simplex|simplex]], i.e. any of its points is the barycentre of a unique [[Probability measure|probability measure]], called the mixing measure, concentrated on the extremal points. This statement remains true for probability measures that are invariant under groups much more general than the (finite) permutations on the natural integers, while the product structure of the extremals seems to be specific to the permutation group. | ||
| − | A slightly tronger statement is as follows: exchangeable random variables are conditionally independent on the | + | A slightly tronger statement is as follows: exchangeable random variables are conditionally independent on the $ \sigma $- |
| + | algebra at infinity. | ||
| − | The following inequality, which might be called the conditional De Finetti theorem and is valid for any finite sequence of exchangeable random variables, explains why De Finetti's theorem (in its stronger formulation) holds exactly if | + | The following inequality, which might be called the conditional De Finetti theorem and is valid for any finite sequence of exchangeable random variables, explains why De Finetti's theorem (in its stronger formulation) holds exactly if $ N = \infty $ |
| + | but only approximately if $ N < \infty $: | ||
| − | + | $$ \tag{a1 } | |
| + | \left \| { {\mathsf E} _ {N} ( b _ {1} \dots b _ {m} ) - {\mathsf E} _ {N} ( b _ {1} ) \dots {\mathsf E} _ {N} ( b _ {m} ) } \right \| \leq | ||
| + | $$ | ||
| − | + | $$ | |
| + | \leq | ||
| + | { | ||
| + | \frac{m ^ {2} }{N} | ||
| + | } \left \| {b _ {1} \dots b _ {m} } \right \| , | ||
| + | $$ | ||
| − | where | + | where $ {\mathsf E} _ {N} $ |
| + | is the conditional expectation onto the $ \sigma $- | ||
| + | algebra generated by the symmetric measurable functions of the first $ N $ | ||
| + | random variables; $ \| \cdot \| $ | ||
| + | is the sup-norm; and $ b _ {j} $ | ||
| + | is a bounded measurable function of the $ j $ | ||
| + | th random variable ( $ 1 \leq j \leq m $). | ||
| + | Intuitively, as $ N \rightarrow \infty $, | ||
| + | $ {\mathsf E} _ {N} \rightarrow {\mathsf E} _ \infty $( | ||
| + | the conditional expectation onto the fixed point $ \sigma $- | ||
| + | algebra of the whole permutation group), while the right-hand side of (a1) tends to zero. Thus, the inequality (a1) implies that $ {\mathsf E} _ \infty $ | ||
| + | factorizes in products of functions of the single random variable. This is the conditional independence asserted in De Finetti's theorem. The triviality of the fixed-point $ \sigma $- | ||
| + | algebra characterizes the extremal symmetric measures which, therefore, also factorize. The Hewitt–Savage lemma, often quoted in connection with De Finetti's theorem, asserts that the fixed-point $ \sigma $- | ||
| + | algebra coincides with the tail $ \sigma $- | ||
| + | algebra, i.e. the fixed-point $ \sigma $- | ||
| + | algebra of the shift (which maps the $ j $ | ||
| + | th random variable into the $ ( j + 1 ) $ | ||
| + | st), whose triviality characterizes ergodic measures (cf. [[Invariant measure|Invariant measure]]). | ||
De Finetti's theorem has been generalized in a number of ways, in particular: | De Finetti's theorem has been generalized in a number of ways, in particular: | ||
| Line 19: | Line 75: | ||
1) for finitely-additive measures ([[#References|[a4]]], cf. also the subtle counterexample in [[#References|[a3]]]); | 1) for finitely-additive measures ([[#References|[a4]]], cf. also the subtle counterexample in [[#References|[a3]]]); | ||
| − | 2) replacing independence by | + | 2) replacing independence by $ m $- |
| + | dependence [[#References|[a5]]]; | ||
3) for Markov chains [[#References|[a2]]]; | 3) for Markov chains [[#References|[a2]]]; | ||
| − | 4) for conditional expectations rather than measures; for a continuous (even multi-dimensional) index set rather than | + | 4) for conditional expectations rather than measures; for a continuous (even multi-dimensional) index set rather than $ \mathbf N $[[#References|[a1]]]; |
5) for measures that are quasi-invariant, rather than invariant, under the permutation group; | 5) for measures that are quasi-invariant, rather than invariant, under the permutation group; | ||
| Line 33: | Line 90: | ||
Since the symmetric random variables are convex combinations of independent identically-distributed random variables, many theorems (e.g. limit theorems) which are valid for the latter continue to be true for the former; however, the corresponding proofs often require additional ingenuity. | Since the symmetric random variables are convex combinations of independent identically-distributed random variables, many theorems (e.g. limit theorems) which are valid for the latter continue to be true for the former; however, the corresponding proofs often require additional ingenuity. | ||
| − | In physics, the main application of De Finetti's theorem is to the so-called mean field models, characterized as follows: One starts from a homogeneous product measure | + | In physics, the main application of De Finetti's theorem is to the so-called mean field models, characterized as follows: One starts from a homogeneous product measure $ \mu _ {o} $, |
| + | called the free measure and interpreted as the distribution of a sequence of independent identically-distributed random variables $ ( X _ {j} ) $. | ||
| + | One perturbs it by a Radon–Nikodým density (Gibbs factor) of the form $ { \mathop{\rm exp} } \{ - H _ {N} \} /Z _ {N} $, | ||
| + | where $ Z _ {N} $ | ||
| + | is a normalization factor and $ H _ {N} $ | ||
| + | is a function of $ X _ {1} + \dots + X _ {N} $. | ||
| + | Such a function is called a mean field type interaction (when the sum is replaced by an arbitrary symmetric function of the $ X _ {j} $' | ||
| + | s, one speaks of generalized mean field models). Under mild growth conditions on the $ H _ {N} $, | ||
| + | the sequence of perturbed probability measures | ||
| − | + | $$ | |
| + | \mu _ {N} = \mu _ {o} \left ( { | ||
| + | \frac{ { \mathop{\rm exp} } \{ - H _ {N} \} }{Z _ {N} } | ||
| + | } \cdot \right ) | ||
| + | $$ | ||
has a limit which is necessarily a symmetric probability measure hence, by De Finetti's theorem, the barycentre of a family of homogeneous product measures. The a priori knowledge of the structure of the limit and the simplicity of this structure allows one to calculate or estimate explicitly many quantities of physical interest. | has a limit which is necessarily a symmetric probability measure hence, by De Finetti's theorem, the barycentre of a family of homogeneous product measures. The a priori knowledge of the structure of the limit and the simplicity of this structure allows one to calculate or estimate explicitly many quantities of physical interest. | ||
| − | The multi-dimensional and the | + | The multi-dimensional and the $ m $- |
| + | dependent versions of De Finetti's theorem have both been proved directly by a quantum probabilistic approach (a further confirmation of the fruitfulness of this approach for most traditional problems in classical probability; cf. [[Quantum probability|Quantum probability]]). | ||
| − | The independent increment stationary processes are the continuous analogue of the independent identically-distributed sequences. Moreover, on the general class of increment processes, i.e. random-variable-valued finitely-additive measures indexed by bounded closed intervals of | + | The independent increment stationary processes are the continuous analogue of the independent identically-distributed sequences. Moreover, on the general class of increment processes, i.e. random-variable-valued finitely-additive measures indexed by bounded closed intervals of $ \mathbf R $, |
| + | one can naturally define an action of the permutation group by permuting among themselves intervals that are translates of each another. An increment process is called exchangeable if it is invariant under the above-mentioned action of the permutation group. The continuous version of De Finetti's theorem asserts that the extremal points of an exchangeable increment process are independent increment stationary processes. With minor verbal changes in the assumptions, the result can be extended by replacing the $ 1 $- | ||
| + | dimensional index set $ \mathbf R $, | ||
| + | acted upon by translations, by a more general topological space acted upon by a more general group. | ||
| − | A natural generalization of the notion of independence is the notion of | + | A natural generalization of the notion of independence is the notion of $ m $- |
| + | dependence. A sequence $ ( X _ {j} ) $ | ||
| + | of random variables is called $ m $- | ||
| + | dependent (cf. [[M-dependent-process| $ m $- | ||
| + | dependent process]]) if the random variables whose indices are more than $ m $ | ||
| + | apart are independent. This means that, for any natural integer $ K $ | ||
| + | and for any sequence of intervals $ [ m _ {1} ,n _ {1} ] \dots [ m _ {K} ,n _ {K} ] \subseteq \mathbf N $ | ||
| + | such that | ||
| − | + | $$ | |
| + | { \mathop{\rm dist} } ( [ m _ \alpha ,n _ \alpha ] , [ m _ {\alpha ^ \prime } ,n _ {\alpha ^ \prime } ] ) \geq m | ||
| + | $$ | ||
| − | if | + | if $ [ m _ \alpha ,n _ \alpha ] \neq [ m _ {\alpha ^ \prime } ,n _ {\alpha ^ \prime } ] $( |
| + | $ \alpha, \alpha ^ \prime = 1 \dots K $), | ||
| + | the blocks of random variables $ ( X _ {j} ) $, | ||
| + | $ j \in [ m _ \alpha ,n _ \alpha ] $, | ||
| + | $ \alpha = 1 \dots K $, | ||
| + | are independent (these definitions are formulated so as to make clear the multi-dimensional generalization). | ||
| − | The sequence | + | The sequence $ ( X _ {j} ) $ |
| + | is called $ m $- | ||
| + | symmetric if, for any $ K \in \mathbf N $ | ||
| + | and for any permutation $ \pi $ | ||
| + | on $ \{ 1 \dots K \} $, | ||
| + | one has | ||
| − | + | $$ | |
| + | \varphi ( a _ {[ \pi ( m _ {1} ) , \pi ( n _ {1} ) ] } \dots a _ {[ \pi ( m _ {K} ) , \pi ( n _ {K} ) ] } ) = | ||
| + | $$ | ||
| − | + | $$ | |
| + | = | ||
| + | \varphi ( a _ {[ m _ {1} ,n _ {1} ] } \dots a _ {[ m _ {K} ,n _ {K} ] } ) | ||
| + | $$ | ||
| − | for any function | + | for any function $ a _ {[ m _ {j} ,n _ {j} ] } $ |
| + | of the random variables $ X _ \alpha $, | ||
| + | $ \alpha \in [ m _ {j} ,n _ {j} ] $( | ||
| + | $ j = 1 \dots K $). | ||
| − | Clearly, | + | Clearly, $ 1 $- |
| + | independence is usual independence. | ||
| − | Denote by | + | Denote by $ {\mathcal S} _ {m} $ |
| + | the set of all shift-invariant $ m $- | ||
| + | symmetric probability measures with the weak topology. The De Finetti theorem for $ m $- | ||
| + | symmetric random variables states that the closed extremal boundary of the compact convex set $ {\mathcal S} _ {m} $ | ||
| + | consists of all the shift-invariant $ m $- | ||
| + | dependent states. Every $ \varphi \in {\mathcal S} _ {m} $ | ||
| + | admits an integral decomposition | ||
| − | + | $$ | |
| + | \varphi ( a ) = \int\limits {p ( a ) } {d \nu ( p ) } ( a \in {\mathcal A} ) | ||
| + | $$ | ||
| − | with a unique probability Radon measure | + | with a unique probability Radon measure $ \nu $ |
| + | on the shift-invariant $ m $- | ||
| + | dependent states. | ||
| − | The proof [[#References|[a5]]] depends on Ressel's characterization of completely positive-definite bounded functions on an Abelian semi-group | + | The proof [[#References|[a5]]] depends on Ressel's characterization of completely positive-definite bounded functions on an Abelian semi-group $ S $, |
| + | [[#References|[a6]]], according to which for any such function there exists a unique Radon measure $ \nu $ | ||
| + | over the space of non-negative semi-characters on $ S $ | ||
| + | such that $ F ( s ) = \int {p ( s ) } {d \nu ( p ) } $. | ||
| + | Recall that, for an Abelian semi-group $ S $ | ||
| + | written additively, a function $ f : S \rightarrow \mathbf C $ | ||
| + | is called completely positive-definite if $ \sum _ {j,k } ^ {n} c _ {j} c _ {k} F ( s + s _ {j} + s _ {k} ) \geq 0 $ | ||
| + | for all $ n \geq 1 $, | ||
| + | $ s,s _ {1} \dots s _ {n} \in S $ | ||
| + | and $ c _ {1} \dots c _ {n} \in \mathbf C $ | ||
| + | and that a semi-character is a function $ p : S \rightarrow \mathbf C $ | ||
| + | for which $ p ( s + t ) = p ( s ) p ( t ) $ | ||
| + | and $ p ( 0 ) = 1 $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L. Accardi, Y.G. Lu, "A continuous version of De Finetti's theorem" ''Ann. of Probab.'' , '''21''' (1993) pp. 1478–1493</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P. Diaconis, D. Freedman, "A dozen De Finetti-style results in search of a theory" ''Ann. Inst. Henri Poincare Suppl. au N.2'' , '''23''' (1987) pp. 397–423</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> L.E. Dubins, D.A. Freedman, "Exchangeable processes need not be mixtures of independent, identically distributed random variables" ''Z. Wahrscheinlichkeitsth. verw. Gebiete'' , '''48''' (1979) pp. 115–132</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> E. Hewitt, L.F. Savage, "Symmetric measures on Cartesian products" ''Trans. Amer. Math. Soc.'' , '''80''' (1955) pp. 470–501</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> D. Petz, "A De Finetti-type theorem with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110020/d110020107.png" />-dependent states" ''Probab. Th. Rel. Fields'' , '''85''' (1990) pp. 65–72</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> P. Ressel, "De Finetti-type theorems: an analytical approach" ''Ann. of Probab.'' , '''13''' (1985) pp. 898–922</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> E. Störmer, "Symmetric states of infinite tensor products of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110020/d110020108.png" />-algebras" ''J. Funct. Anal.'' , '''3''' (1969) pp. 48–68</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> ?. Bühlman, "Austauschbare Stochastische Variablen und ihre Grenzwertsatze" ''Univ. California Publ. Stat.'' (1960) pp. 31–36</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> D.A. Freedman, "Invariance under mixing which generalize De Finetti's theorem: continuous time parameter" ''Ann. Math. Stat.'' , '''33''' (1962) pp. 916–923</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> D.A. Freedman, "Invariance under mixing which generalize De Finetti's theorem: continuous time parameter" ''Ann. Math. Stat.'' , '''34''' (1963) pp. 1194–1216</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L. Accardi, Y.G. Lu, "A continuous version of De Finetti's theorem" ''Ann. of Probab.'' , '''21''' (1993) pp. 1478–1493</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P. Diaconis, D. Freedman, "A dozen De Finetti-style results in search of a theory" ''Ann. Inst. Henri Poincare Suppl. au N.2'' , '''23''' (1987) pp. 397–423</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> L.E. Dubins, D.A. Freedman, "Exchangeable processes need not be mixtures of independent, identically distributed random variables" ''Z. Wahrscheinlichkeitsth. verw. Gebiete'' , '''48''' (1979) pp. 115–132</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> E. Hewitt, L.F. Savage, "Symmetric measures on Cartesian products" ''Trans. Amer. Math. Soc.'' , '''80''' (1955) pp. 470–501</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> D. Petz, "A De Finetti-type theorem with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110020/d110020107.png" />-dependent states" ''Probab. Th. Rel. Fields'' , '''85''' (1990) pp. 65–72</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> P. Ressel, "De Finetti-type theorems: an analytical approach" ''Ann. of Probab.'' , '''13''' (1985) pp. 898–922</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> E. Störmer, "Symmetric states of infinite tensor products of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110020/d110020108.png" />-algebras" ''J. Funct. Anal.'' , '''3''' (1969) pp. 48–68</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> ?. Bühlman, "Austauschbare Stochastische Variablen und ihre Grenzwertsatze" ''Univ. California Publ. Stat.'' (1960) pp. 31–36</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> D.A. Freedman, "Invariance under mixing which generalize De Finetti's theorem: continuous time parameter" ''Ann. Math. Stat.'' , '''33''' (1962) pp. 916–923</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> D.A. Freedman, "Invariance under mixing which generalize De Finetti's theorem: continuous time parameter" ''Ann. Math. Stat.'' , '''34''' (1963) pp. 1194–1216</TD></TR></table> | ||
Revision as of 17:32, 5 June 2020
Consider a sequence of $ N $
independent identically-distributed random variables $ ( X _ {j} ) $,
$ j = 1 \dots N $,
with $ N \leq \infty $(
cf. Random variable). Clearly, their law is invariant under permutation, i.e. for any finite subset $ F $
of $ \{ 1 \dots N \} $
and for any permutation $ \pi $
of $ F $,
the joint distribution of $ ( X _ {\pi ( j ) } ) $(
$ j \in F $)
is the same as the joint distribution of $ ( X _ {j} ) $(
$ j \in F $).
Denoting by $ P $
the joint law of the $ ( X _ {j} ) $'
s, one can express the above-stated invariance property as follows: $ P \circ \pi = P $.
Clearly, this property of $ P $
is preserved under convex combinations. A sequence of random variables (or, equivalently, their probability distribution) whose finite-dimensional joint laws are invariant under permutations is called exchangeable or symmetric.
The following question may be asked: Are the convex combinations of laws of independent identically-distributed random variables the only exchangeable probability measures? The answer is no if $ N < \infty $, and yes if $ N = \infty $. The latter statement is De Finetti's theorem. Thus, an equivalent statement of De Finetti's theorem is that the extremal points of the convex set of exchangeable probability measures on an infinite product space are the laws of sequences of independent identically-distributed random variables.
De Finetti's theorem asserts, moreover, that this convex set is a simplex, i.e. any of its points is the barycentre of a unique probability measure, called the mixing measure, concentrated on the extremal points. This statement remains true for probability measures that are invariant under groups much more general than the (finite) permutations on the natural integers, while the product structure of the extremals seems to be specific to the permutation group.
A slightly tronger statement is as follows: exchangeable random variables are conditionally independent on the $ \sigma $- algebra at infinity.
The following inequality, which might be called the conditional De Finetti theorem and is valid for any finite sequence of exchangeable random variables, explains why De Finetti's theorem (in its stronger formulation) holds exactly if $ N = \infty $ but only approximately if $ N < \infty $:
$$ \tag{a1 } \left \| { {\mathsf E} _ {N} ( b _ {1} \dots b _ {m} ) - {\mathsf E} _ {N} ( b _ {1} ) \dots {\mathsf E} _ {N} ( b _ {m} ) } \right \| \leq $$
$$ \leq { \frac{m ^ {2} }{N} } \left \| {b _ {1} \dots b _ {m} } \right \| , $$
where $ {\mathsf E} _ {N} $ is the conditional expectation onto the $ \sigma $- algebra generated by the symmetric measurable functions of the first $ N $ random variables; $ \| \cdot \| $ is the sup-norm; and $ b _ {j} $ is a bounded measurable function of the $ j $ th random variable ( $ 1 \leq j \leq m $). Intuitively, as $ N \rightarrow \infty $, $ {\mathsf E} _ {N} \rightarrow {\mathsf E} _ \infty $( the conditional expectation onto the fixed point $ \sigma $- algebra of the whole permutation group), while the right-hand side of (a1) tends to zero. Thus, the inequality (a1) implies that $ {\mathsf E} _ \infty $ factorizes in products of functions of the single random variable. This is the conditional independence asserted in De Finetti's theorem. The triviality of the fixed-point $ \sigma $- algebra characterizes the extremal symmetric measures which, therefore, also factorize. The Hewitt–Savage lemma, often quoted in connection with De Finetti's theorem, asserts that the fixed-point $ \sigma $- algebra coincides with the tail $ \sigma $- algebra, i.e. the fixed-point $ \sigma $- algebra of the shift (which maps the $ j $ th random variable into the $ ( j + 1 ) $ st), whose triviality characterizes ergodic measures (cf. Invariant measure).
De Finetti's theorem has been generalized in a number of ways, in particular:
1) for finitely-additive measures ([a4], cf. also the subtle counterexample in [a3]);
2) replacing independence by $ m $- dependence [a5];
3) for Markov chains [a2];
4) for conditional expectations rather than measures; for a continuous (even multi-dimensional) index set rather than $ \mathbf N $[a1];
5) for measures that are quasi-invariant, rather than invariant, under the permutation group;
6) to quantum versions [a7].
Moreover, active research is still (1996) devoted to the problem of characterizing the extremal points of various types of symmetric finite sequences of random variables, the so-called finite De Finetti theorem.
Since the symmetric random variables are convex combinations of independent identically-distributed random variables, many theorems (e.g. limit theorems) which are valid for the latter continue to be true for the former; however, the corresponding proofs often require additional ingenuity.
In physics, the main application of De Finetti's theorem is to the so-called mean field models, characterized as follows: One starts from a homogeneous product measure $ \mu _ {o} $, called the free measure and interpreted as the distribution of a sequence of independent identically-distributed random variables $ ( X _ {j} ) $. One perturbs it by a Radon–Nikodým density (Gibbs factor) of the form $ { \mathop{\rm exp} } \{ - H _ {N} \} /Z _ {N} $, where $ Z _ {N} $ is a normalization factor and $ H _ {N} $ is a function of $ X _ {1} + \dots + X _ {N} $. Such a function is called a mean field type interaction (when the sum is replaced by an arbitrary symmetric function of the $ X _ {j} $' s, one speaks of generalized mean field models). Under mild growth conditions on the $ H _ {N} $, the sequence of perturbed probability measures
$$ \mu _ {N} = \mu _ {o} \left ( { \frac{ { \mathop{\rm exp} } \{ - H _ {N} \} }{Z _ {N} } } \cdot \right ) $$
has a limit which is necessarily a symmetric probability measure hence, by De Finetti's theorem, the barycentre of a family of homogeneous product measures. The a priori knowledge of the structure of the limit and the simplicity of this structure allows one to calculate or estimate explicitly many quantities of physical interest.
The multi-dimensional and the $ m $- dependent versions of De Finetti's theorem have both been proved directly by a quantum probabilistic approach (a further confirmation of the fruitfulness of this approach for most traditional problems in classical probability; cf. Quantum probability).
The independent increment stationary processes are the continuous analogue of the independent identically-distributed sequences. Moreover, on the general class of increment processes, i.e. random-variable-valued finitely-additive measures indexed by bounded closed intervals of $ \mathbf R $, one can naturally define an action of the permutation group by permuting among themselves intervals that are translates of each another. An increment process is called exchangeable if it is invariant under the above-mentioned action of the permutation group. The continuous version of De Finetti's theorem asserts that the extremal points of an exchangeable increment process are independent increment stationary processes. With minor verbal changes in the assumptions, the result can be extended by replacing the $ 1 $- dimensional index set $ \mathbf R $, acted upon by translations, by a more general topological space acted upon by a more general group.
A natural generalization of the notion of independence is the notion of $ m $- dependence. A sequence $ ( X _ {j} ) $ of random variables is called $ m $- dependent (cf. $ m $- dependent process) if the random variables whose indices are more than $ m $ apart are independent. This means that, for any natural integer $ K $ and for any sequence of intervals $ [ m _ {1} ,n _ {1} ] \dots [ m _ {K} ,n _ {K} ] \subseteq \mathbf N $ such that
$$ { \mathop{\rm dist} } ( [ m _ \alpha ,n _ \alpha ] , [ m _ {\alpha ^ \prime } ,n _ {\alpha ^ \prime } ] ) \geq m $$
if $ [ m _ \alpha ,n _ \alpha ] \neq [ m _ {\alpha ^ \prime } ,n _ {\alpha ^ \prime } ] $( $ \alpha, \alpha ^ \prime = 1 \dots K $), the blocks of random variables $ ( X _ {j} ) $, $ j \in [ m _ \alpha ,n _ \alpha ] $, $ \alpha = 1 \dots K $, are independent (these definitions are formulated so as to make clear the multi-dimensional generalization).
The sequence $ ( X _ {j} ) $ is called $ m $- symmetric if, for any $ K \in \mathbf N $ and for any permutation $ \pi $ on $ \{ 1 \dots K \} $, one has
$$ \varphi ( a _ {[ \pi ( m _ {1} ) , \pi ( n _ {1} ) ] } \dots a _ {[ \pi ( m _ {K} ) , \pi ( n _ {K} ) ] } ) = $$
$$ = \varphi ( a _ {[ m _ {1} ,n _ {1} ] } \dots a _ {[ m _ {K} ,n _ {K} ] } ) $$
for any function $ a _ {[ m _ {j} ,n _ {j} ] } $ of the random variables $ X _ \alpha $, $ \alpha \in [ m _ {j} ,n _ {j} ] $( $ j = 1 \dots K $).
Clearly, $ 1 $- independence is usual independence.
Denote by $ {\mathcal S} _ {m} $ the set of all shift-invariant $ m $- symmetric probability measures with the weak topology. The De Finetti theorem for $ m $- symmetric random variables states that the closed extremal boundary of the compact convex set $ {\mathcal S} _ {m} $ consists of all the shift-invariant $ m $- dependent states. Every $ \varphi \in {\mathcal S} _ {m} $ admits an integral decomposition
$$ \varphi ( a ) = \int\limits {p ( a ) } {d \nu ( p ) } ( a \in {\mathcal A} ) $$
with a unique probability Radon measure $ \nu $ on the shift-invariant $ m $- dependent states.
The proof [a5] depends on Ressel's characterization of completely positive-definite bounded functions on an Abelian semi-group $ S $, [a6], according to which for any such function there exists a unique Radon measure $ \nu $ over the space of non-negative semi-characters on $ S $ such that $ F ( s ) = \int {p ( s ) } {d \nu ( p ) } $. Recall that, for an Abelian semi-group $ S $ written additively, a function $ f : S \rightarrow \mathbf C $ is called completely positive-definite if $ \sum _ {j,k } ^ {n} c _ {j} c _ {k} F ( s + s _ {j} + s _ {k} ) \geq 0 $ for all $ n \geq 1 $, $ s,s _ {1} \dots s _ {n} \in S $ and $ c _ {1} \dots c _ {n} \in \mathbf C $ and that a semi-character is a function $ p : S \rightarrow \mathbf C $ for which $ p ( s + t ) = p ( s ) p ( t ) $ and $ p ( 0 ) = 1 $.
References
| [a1] | L. Accardi, Y.G. Lu, "A continuous version of De Finetti's theorem" Ann. of Probab. , 21 (1993) pp. 1478–1493 |
| [a2] | P. Diaconis, D. Freedman, "A dozen De Finetti-style results in search of a theory" Ann. Inst. Henri Poincare Suppl. au N.2 , 23 (1987) pp. 397–423 |
| [a3] | L.E. Dubins, D.A. Freedman, "Exchangeable processes need not be mixtures of independent, identically distributed random variables" Z. Wahrscheinlichkeitsth. verw. Gebiete , 48 (1979) pp. 115–132 |
| [a4] | E. Hewitt, L.F. Savage, "Symmetric measures on Cartesian products" Trans. Amer. Math. Soc. , 80 (1955) pp. 470–501 |
| [a5] | D. Petz, "A De Finetti-type theorem with  -dependent states" Probab. Th. Rel. Fields , 85 (1990) pp. 65–72 -dependent states" Probab. Th. Rel. Fields , 85 (1990) pp. 65–72 |
| [a6] | P. Ressel, "De Finetti-type theorems: an analytical approach" Ann. of Probab. , 13 (1985) pp. 898–922 |
| [a7] | E. Störmer, "Symmetric states of infinite tensor products of 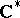 -algebras" J. Funct. Anal. , 3 (1969) pp. 48–68 -algebras" J. Funct. Anal. , 3 (1969) pp. 48–68 |
| [a8] | ?. Bühlman, "Austauschbare Stochastische Variablen und ihre Grenzwertsatze" Univ. California Publ. Stat. (1960) pp. 31–36 |
| [a9] | D.A. Freedman, "Invariance under mixing which generalize De Finetti's theorem: continuous time parameter" Ann. Math. Stat. , 33 (1962) pp. 916–923 |
| [a10] | D.A. Freedman, "Invariance under mixing which generalize De Finetti's theorem: continuous time parameter" Ann. Math. Stat. , 34 (1963) pp. 1194–1216 |
De Finetti theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=De_Finetti_theorem&oldid=12884