Difference between revisions of "Cyclotomic field"
m (link) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | c0275701.png | ||
| + | $#A+1 = 151 n = 3 | ||
| + | $#C+1 = 151 : ~/encyclopedia/old_files/data/C027/C.0207570 Cyclotomic field, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | The special position of cyclotomic fields among all algebraic number fields is illustrated by the [[Kronecker–Weber theorem]], which states that a finite extension | + | A field $ K _ {n} = \mathbf Q ( \zeta _ {n} ) $ |
| + | obtained from the field $ \mathbf Q $ | ||
| + | of rational numbers by adjoining a primitive $ n $- | ||
| + | th root of unity $ \zeta _ {n} $, | ||
| + | where $ n $ | ||
| + | is a natural number. The term (local) cyclotomic field is also sometimes applied to the fields $ \mathbf Q _ {p} ( \zeta _ {n} ) $, | ||
| + | where $ \mathbf Q _ {p} $ | ||
| + | is the field of rational $ p $- | ||
| + | adic numbers. Since $ K _ {n} = K _ {2n} $ | ||
| + | when $ n $ | ||
| + | is odd, it is usually assumed that $ n \not\equiv 2 $( | ||
| + | $ \mathop{\rm mod} 4 $). | ||
| + | Distinct $ n $ | ||
| + | then correspond to non-isomorphic fields $ K _ {n} $. | ||
| + | |||
| + | Cyclotomic fields arise naturally in the cyclotomy problem — the division of a circle into $ n $ | ||
| + | equal parts is equivalent to the construction of a primitive root $ \zeta _ {n} $ | ||
| + | in the complex plane. The structure of cyclotomic fields is "fairly simple" , and they therefore provide convenient experimental material in formulating general concepts in number theory. For example, the concept of an algebraic integer and a divisor first arose in the study of cyclotomic fields. | ||
| + | |||
| + | The special position of cyclotomic fields among all algebraic number fields is illustrated by the [[Kronecker–Weber theorem]], which states that a finite extension $ K/ \mathbf Q $ | ||
| + | is Abelian if and only if $ K \subset K _ {n} $ | ||
| + | for some $ n $. | ||
| + | An analogous proposition holds for local cyclotomic fields. | ||
==Algebraic theory.== | ==Algebraic theory.== | ||
| − | The field | + | The field $ K _ {n} $ |
| + | is an Abelian extension of $ \mathbf Q $ | ||
| + | with Galois group | ||
| − | + | $$ | |
| + | G ( K _ {n} / \mathbf Q ) \simeq \ | ||
| + | ( \mathbf Z /n \mathbf Z ) ^ {*} , | ||
| + | $$ | ||
| − | where | + | where $ ( \mathbf Z /n \mathbf Z ) ^ {*} $ |
| + | is the multiplicative group of the ring of residues modulo $ n $. | ||
| + | In particular, the degree $ [ K _ {n} : \mathbf Q ] $ | ||
| + | is $ \phi ( n) $, | ||
| + | where $ \phi ( n) $ | ||
| + | is Euler's function. The field $ K _ {n} $ | ||
| + | is totally imaginary and of degree 2 over its maximal totally real subfield $ K _ {n} ^ {+} = \mathbf Q ( \zeta _ {n} + \zeta _ {n} ^ {-} 1 ) $. | ||
| − | If | + | If $ n = p _ {1} ^ {t _ {1} } \dots p _ {s} ^ {t _ {s} } $ |
| + | is the factorization of $ n $ | ||
| + | into prime numbers, then $ K _ {n} $ | ||
| + | is the linearly disjoint compositum of the fields $ K _ {p _ {1} ^ {t _ {1} } } \dots K _ {p _ {s} ^ {t _ {s} } } $. | ||
| + | In the field $ K _ {p ^ {t} } $ | ||
| + | the prime divisor $ p $ | ||
| + | has ramification index $ e = ( p - 1) p ^ {t - 1 } = \phi ( p ^ {t} ) $. | ||
| + | In the same field one has the following equality of principal divisors: $ ( p) = ( 1 - \zeta _ {p ^ {t} } ) ^ {e} $. | ||
| + | All other prime divisors of $ \mathbf Q $ | ||
| + | are unramified in $ K _ {p ^ {t} } $, | ||
| + | whence it follows that $ p $ | ||
| + | is ramified in $ K _ {n} $ | ||
| + | if and only if $ p\mid n $. | ||
| − | The numbers | + | The numbers $ 1, \zeta _ {n} \dots \zeta _ {n} ^ {\phi ( n) - 1 } $ |
| + | form an integral basis for the field $ K _ {n} $. | ||
| + | The discriminant of $ K _ {p ^ {t} } $ | ||
| + | is equal to $ \pm p ^ {p ^ {t - 1 } ( pt - t - 1) } $. | ||
| + | If $ E $ | ||
| + | and $ F $ | ||
| + | are fields which are linearly disjoint over $ \mathbf Q $ | ||
| + | with relatively prime discriminants $ D _ {E} $ | ||
| + | and $ D _ {F} $, | ||
| + | then $ D _ {EF} = D _ {E} ^ {n} D _ {F} ^ {m} $, | ||
| + | where $ n = [ F: \mathbf Q ] $, | ||
| + | $ m = [ E: \mathbf Q ] $. | ||
| + | This makes it possible to calculate $ D _ {K _ {n} } $ | ||
| + | for arbitrary $ n $( | ||
| + | see [[#References|[3]]]). | ||
| − | For the field | + | For the field $ K _ {p ^ {t} } $, |
| + | the numbers | ||
| − | + | $$ | |
| − | + | \frac{( 1 - \zeta _ {p ^ {t} } ^ {a} ) }{( 1 - \zeta _ {p ^ {t} } | |
| + | ^ {b} ) } | ||
| + | , | ||
| + | $$ | ||
| − | + | where $ a, b \not\equiv 0 ( \mathop{\rm mod} p) $, | |
| + | generate a subgroup of finite index in the group of all units. The elements of this subgroup are known as circular units or cyclotomic units. | ||
| − | + | The decomposition law for cyclotomic fields, that is, the law according to which the prime divisors $ ( p) $ | |
| + | in $ \mathbf Q $ | ||
| + | factorize into prime divisors in $ K _ {n} $, | ||
| + | is a particular case of the general decomposition law in Abelian extensions, established in class field theory (see [[#References|[4]]]). Explicitly: If $ ( p, n) = 1 $ | ||
| + | and if $ f $ | ||
| + | is the least natural number such that $ p ^ {f} \equiv 1 $( | ||
| + | $ \mathop{\rm mod} n $), | ||
| + | then in $ K _ {n} $, | ||
| − | + | $$ | |
| + | ( p) = \ | ||
| + | \mathfrak p _ {1} \dots \mathfrak p _ {g} , | ||
| + | $$ | ||
| − | + | where the prime divisors $ \mathfrak p _ {1} \dots \mathfrak p _ {g} $ | |
| + | are pairwise distinct, $ N ( \mathfrak p _ {i} ) = p ^ {f} $ | ||
| + | and $ fg = \phi ( n) $. | ||
| + | Thus, the factorization type of $ ( p) $ | ||
| + | depends only on the residue of $ p $( | ||
| + | $ \mathop{\rm mod} n $). | ||
| + | If $ p\mid n $, | ||
| + | the exact form of the factorization of $ ( p) $ | ||
| + | can be obtained, using the facts that $ K _ {n} = K _ {m} K _ {p ^ {t} } $, | ||
| + | where $ ( m, p) = 1 $ | ||
| + | and $ ( p) $ | ||
| + | is totally ramified in $ K _ {p ^ {t} } $. | ||
| − | + | If $ K $ | |
| + | is the maximal Abelian extension of $ \mathbf Q $, | ||
| + | then $ K = \cup _ {n} K _ {n} $ | ||
| + | and | ||
| − | + | $$ | |
| + | G ( K/ \mathbf Q ) \simeq \ | ||
| + | \lim\limits _ \leftarrow G ( K _ {n} / \mathbf Q ) \simeq \ | ||
| + | \lim\limits ( \mathbf Z /n \mathbf Z ) ^ {*} \simeq \ | ||
| + | \widehat{\mathbf Z} {} ^ {*} , | ||
| + | $$ | ||
| + | |||
| + | where $ \widehat{\mathbf Z} $ | ||
| + | is the completion of the ring of integers $ \mathbf Z $ | ||
| + | with respect to all ideals of finite index. In particular, for any prime number $ l $ | ||
| + | there is a unique extension $ \mathbf Q _ {\infty , l } / \mathbf Q $ | ||
| + | with Galois group isomorphic to the group of $ l $- | ||
| + | adic integers $ \mathbf Z _ {l} $. | ||
According to [[Class field theory|class field theory]], there exists a reciprocity map | According to [[Class field theory|class field theory]], there exists a reciprocity map | ||
| − | + | $$ | |
| + | \psi : J _ {\mathbf Q} \rightarrow \ | ||
| + | G ( K/ \mathbf Q ), | ||
| + | $$ | ||
| − | where | + | where $ J _ {\mathbf Q} $ |
| + | is the idèle group of $ \mathbf Q $. | ||
| + | In the case of a cyclotomic field $ \psi $ | ||
| + | admits a simple explicit description (see [[#References|[4]]]). | ||
==Analytic theory.== | ==Analytic theory.== | ||
| − | Many results regarding the structure of the divisor class group of | + | Many results regarding the structure of the divisor class group of $ K _ {n} $ |
| + | can be proved by analytic methods. If $ h _ {n} $ | ||
| + | is the class number of $ K _ {n} $, | ||
| + | then | ||
| − | + | $$ | |
| + | h _ {n} = \ | ||
| + | 2 ^ {-} t \pi ^ {-} t R ^ {-} 1 w | ||
| + | \sqrt {| D | } | ||
| + | \prod _ {\chi \neq \chi _ {0} } | ||
| + | L ( 1, \chi ), | ||
| + | $$ | ||
| − | here | + | here $ w, D $ |
| + | and $ R $ | ||
| + | are, respectively, the number of roots of unity, the discriminant and the regulator of $ K _ {n} $, | ||
| + | $ t = \phi ( n)/2 $, | ||
| + | and $ L ( 1, \chi ) $ | ||
| + | is the Dirichlet $ L $- | ||
| + | function for the character $ \chi $, | ||
| + | where $ \chi $ | ||
| + | runs through all non-trivial primitive multiplicative characters modulo $ n $. | ||
| + | The function $ L ( 1, \chi ) $ | ||
| + | in turn can be expressed explicitly in terms of Gauss sums (see [[#References|[7]]]). This solves the problem of calculating $ h _ {n} $, | ||
| + | given $ n $. | ||
| − | There is a natural decomposition of | + | There is a natural decomposition of $ h _ {n} $ |
| + | into two factors, $ h _ {n} = h _ {n} ^ {-} h _ {n} ^ {+} $; | ||
| + | the first and second factor of the class number, where $ h _ {n} ^ {+} $ | ||
| + | is interpreted as the class number of the field $ K _ {n} ^ {+} $. | ||
| + | If $ n = p ^ {t} $ | ||
| + | then $ h _ {n} ^ {+} = [ E : E _ {0} ] $, | ||
| + | where $ E $ | ||
| + | is the group of units of $ K _ {p ^ {t} } ^ {+} $ | ||
| + | and $ E _ {0} $ | ||
| + | is the group of real cyclotomic units (any cyclotomic unit becomes real if multiplied by a suitable root of unity). | ||
| − | In questions related to the Fermat problem, an important role is played by the divisibility of the class number of | + | In questions related to the Fermat problem, an important role is played by the divisibility of the class number of $ K _ {l} $ |
| + | by $ l $, | ||
| + | where $ l $ | ||
| + | is prime. It is known that $ h _ {l} \equiv 0 $( | ||
| + | $ \mathop{\rm mod} l $) | ||
| + | for infinitely many prime numbers $ l $( | ||
| + | such numbers $ l $ | ||
| + | are said to be irregular). As to the set of regular prime numbers $ l $, | ||
| + | i.e. numbers for which $ h _ {l} \not\equiv 0 $( | ||
| + | $ \mathop{\rm mod} l $), | ||
| + | it is not known (1982) whether it is finite or infinite. It has been conjectured that $ h _ {l} ^ {+} \not\equiv 0 $( | ||
| + | $ \mathop{\rm mod} l $) | ||
| + | for all $ l $, | ||
| + | and this has been confirmed in a large number of cases. The factor $ h _ {l} ^ {-} $ | ||
| + | is more amenable to investigation. There exists a relatively simple criterion for the divisibility of $ h _ {l} ^ {-} $( | ||
| + | and $ h _ {l} $) | ||
| + | by $ l $ | ||
| + | in terms of Bernoulli numbers ([[#References|[7]]]). It is known that $ h _ {l} ^ {-} \rightarrow \infty $ | ||
| + | as $ l \rightarrow \infty $ | ||
| + | and that $ h _ {l} = 1 $ | ||
| + | if and only if $ l \leq 19 $( | ||
| + | see [[#References|[6]]]). | ||
| − | The so-called | + | The so-called $ p $- |
| + | adic $ L $- | ||
| + | functions have been successfully applied to the study of the class groups of cyclotomic fields (see [[#References|[5]]], [[#References|[8]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> E. Kummer, "Ueber die Zerlegung der aus Wurzeln der Einheit gebildeten komplexen Zahlen in ihre Primfaktoren" ''J. Reine Angew. Math.'' , '''35''' (1847) pp. 327–367</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Weyl, "Algebraic theory of numbers" , Princeton Univ. Press (1959) {{MR|1617068}} {{MR|0002354}} {{ZBL|0921.11001}} {{ZBL|0063.08223}} {{ZBL|0054.02002}} {{ZBL|66.1210.02}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S. Lang, "Algebraic number theory" , Addison-Wesley (1970) {{MR|0282947}} {{ZBL|0211.38404}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> J.W.S. Cassels (ed.) A. Fröhlich (ed.) , ''Algebraic number theory'' , Acad. Press (1967) {{MR|0215665}} {{ZBL|0153.07403}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> I.R. Shafarevich, "The zeta-function" , Moscow (1969) (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> K. Uchida, "Class numbers of imaginary abelian number fields III" ''Tôhoku Math. J.'' , '''23''' (1971) pp. 573–580 {{MR|0288097}} {{ZBL|0241.12002}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1975) (Translated from Russian) (German translation: Birkhäuser, 1966) {{MR|1355542}} {{MR|1534414}} {{MR|0195803}} {{ZBL|0614.00005}} {{ZBL|0592.12001}} {{ZBL|0145.04901}} {{ZBL|0145.04902}} {{ZBL|0121.04202}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> K. Iwasawa, "Lectures on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027570/c027570143.png" />-adic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027570/c027570144.png" />-functions" , Springer (1972) {{MR|360526}} {{ZBL|}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> S. Lang, "Cyclotomic fields" , Springer (1978) {{MR|0485768}} {{ZBL|0395.12005}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E. Kummer, "Ueber die Zerlegung der aus Wurzeln der Einheit gebildeten komplexen Zahlen in ihre Primfaktoren" ''J. Reine Angew. Math.'' , '''35''' (1847) pp. 327–367</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Weyl, "Algebraic theory of numbers" , Princeton Univ. Press (1959) {{MR|1617068}} {{MR|0002354}} {{ZBL|0921.11001}} {{ZBL|0063.08223}} {{ZBL|0054.02002}} {{ZBL|66.1210.02}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S. Lang, "Algebraic number theory" , Addison-Wesley (1970) {{MR|0282947}} {{ZBL|0211.38404}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> J.W.S. Cassels (ed.) A. Fröhlich (ed.) , ''Algebraic number theory'' , Acad. Press (1967) {{MR|0215665}} {{ZBL|0153.07403}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> I.R. Shafarevich, "The zeta-function" , Moscow (1969) (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> K. Uchida, "Class numbers of imaginary abelian number fields III" ''Tôhoku Math. J.'' , '''23''' (1971) pp. 573–580 {{MR|0288097}} {{ZBL|0241.12002}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1975) (Translated from Russian) (German translation: Birkhäuser, 1966) {{MR|1355542}} {{MR|1534414}} {{MR|0195803}} {{ZBL|0614.00005}} {{ZBL|0592.12001}} {{ZBL|0145.04901}} {{ZBL|0145.04902}} {{ZBL|0121.04202}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> K. Iwasawa, "Lectures on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027570/c027570143.png" />-adic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027570/c027570144.png" />-functions" , Springer (1972) {{MR|360526}} {{ZBL|}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> S. Lang, "Cyclotomic fields" , Springer (1978) {{MR|0485768}} {{ZBL|0395.12005}} </TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | It is still not known whether there are infinitely many regular primes (1987), but it is conjectured that the density of the set of regular primes inside the set of all primes is | + | It is still not known whether there are infinitely many regular primes (1987), but it is conjectured that the density of the set of regular primes inside the set of all primes is $ e ^ {-} 1/2 \approx 0.6065 $, |
| + | see [[#References|[a5]]]. It has been proved (for $ n \not\equiv 2 $ | ||
| + | $ \mathop{\rm mod} 4 $) | ||
| + | that $ h _ {n} = 1 $ | ||
| + | if and only if $ \phi ( n) \leq 20 $ | ||
| + | or $ n = 35, 45 $ | ||
| + | or $ 84 $, | ||
| + | see [[#References|[a3]]], [[#References|[a5]]]. An important theorem that describes the structure of the class groups of cyclotomic fields in terms of $ p $- | ||
| + | adic $ L $- | ||
| + | functions has been proved by B. Mazur and A. Wiles (see [[#References|[a1]]], [[#References|[a4]]]) with the help of methods from algebraic geometry. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Coates, "The work of Mazur and Wiles on cyclotomic fields." ''Sem. Bourbaki'' , '''33''' : 575 (1980/81) ''Lecture Notes in Math.'' , '''901''' (1981) pp. 220–242 {{MR|0647499}} {{ZBL|0506.12001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> S. Lang, "Cyclotomic fields" , '''II''' , Springer (1980) {{MR|0566952}} {{ZBL|0435.12001}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J.M. Masley, H.L. Montgomery, "Cyclotomic fields with unique factorization" ''J. Reine Angew. Math.'' , '''286–287''' (1976) pp. 248–256 {{MR|0429824}} {{ZBL|0335.12013}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> B. Mazur, A. Wiles, "Class fields of abelian extensions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027570/c027570154.png" />" ''Invent. Math.'' , '''76''' (1984) pp. 179–330 {{MR|0742853}} {{ZBL|0545.12005}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> L.C. Washington, "Cyclotomic fields" , Springer (1982) {{MR|0718674}} {{ZBL|0502.12003}} {{ZBL|0484.12001}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Coates, "The work of Mazur and Wiles on cyclotomic fields." ''Sem. Bourbaki'' , '''33''' : 575 (1980/81) ''Lecture Notes in Math.'' , '''901''' (1981) pp. 220–242 {{MR|0647499}} {{ZBL|0506.12001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> S. Lang, "Cyclotomic fields" , '''II''' , Springer (1980) {{MR|0566952}} {{ZBL|0435.12001}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J.M. Masley, H.L. Montgomery, "Cyclotomic fields with unique factorization" ''J. Reine Angew. Math.'' , '''286–287''' (1976) pp. 248–256 {{MR|0429824}} {{ZBL|0335.12013}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> B. Mazur, A. Wiles, "Class fields of abelian extensions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027570/c027570154.png" />" ''Invent. Math.'' , '''76''' (1984) pp. 179–330 {{MR|0742853}} {{ZBL|0545.12005}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> L.C. Washington, "Cyclotomic fields" , Springer (1982) {{MR|0718674}} {{ZBL|0502.12003}} {{ZBL|0484.12001}} </TD></TR></table> | ||
Revision as of 17:31, 5 June 2020
A field $ K _ {n} = \mathbf Q ( \zeta _ {n} ) $
obtained from the field $ \mathbf Q $
of rational numbers by adjoining a primitive $ n $-
th root of unity $ \zeta _ {n} $,
where $ n $
is a natural number. The term (local) cyclotomic field is also sometimes applied to the fields $ \mathbf Q _ {p} ( \zeta _ {n} ) $,
where $ \mathbf Q _ {p} $
is the field of rational $ p $-
adic numbers. Since $ K _ {n} = K _ {2n} $
when $ n $
is odd, it is usually assumed that $ n \not\equiv 2 $(
$ \mathop{\rm mod} 4 $).
Distinct $ n $
then correspond to non-isomorphic fields $ K _ {n} $.
Cyclotomic fields arise naturally in the cyclotomy problem — the division of a circle into $ n $ equal parts is equivalent to the construction of a primitive root $ \zeta _ {n} $ in the complex plane. The structure of cyclotomic fields is "fairly simple" , and they therefore provide convenient experimental material in formulating general concepts in number theory. For example, the concept of an algebraic integer and a divisor first arose in the study of cyclotomic fields.
The special position of cyclotomic fields among all algebraic number fields is illustrated by the Kronecker–Weber theorem, which states that a finite extension $ K/ \mathbf Q $ is Abelian if and only if $ K \subset K _ {n} $ for some $ n $. An analogous proposition holds for local cyclotomic fields.
Algebraic theory.
The field $ K _ {n} $ is an Abelian extension of $ \mathbf Q $ with Galois group
$$ G ( K _ {n} / \mathbf Q ) \simeq \ ( \mathbf Z /n \mathbf Z ) ^ {*} , $$
where $ ( \mathbf Z /n \mathbf Z ) ^ {*} $ is the multiplicative group of the ring of residues modulo $ n $. In particular, the degree $ [ K _ {n} : \mathbf Q ] $ is $ \phi ( n) $, where $ \phi ( n) $ is Euler's function. The field $ K _ {n} $ is totally imaginary and of degree 2 over its maximal totally real subfield $ K _ {n} ^ {+} = \mathbf Q ( \zeta _ {n} + \zeta _ {n} ^ {-} 1 ) $.
If $ n = p _ {1} ^ {t _ {1} } \dots p _ {s} ^ {t _ {s} } $ is the factorization of $ n $ into prime numbers, then $ K _ {n} $ is the linearly disjoint compositum of the fields $ K _ {p _ {1} ^ {t _ {1} } } \dots K _ {p _ {s} ^ {t _ {s} } } $. In the field $ K _ {p ^ {t} } $ the prime divisor $ p $ has ramification index $ e = ( p - 1) p ^ {t - 1 } = \phi ( p ^ {t} ) $. In the same field one has the following equality of principal divisors: $ ( p) = ( 1 - \zeta _ {p ^ {t} } ) ^ {e} $. All other prime divisors of $ \mathbf Q $ are unramified in $ K _ {p ^ {t} } $, whence it follows that $ p $ is ramified in $ K _ {n} $ if and only if $ p\mid n $.
The numbers $ 1, \zeta _ {n} \dots \zeta _ {n} ^ {\phi ( n) - 1 } $ form an integral basis for the field $ K _ {n} $. The discriminant of $ K _ {p ^ {t} } $ is equal to $ \pm p ^ {p ^ {t - 1 } ( pt - t - 1) } $. If $ E $ and $ F $ are fields which are linearly disjoint over $ \mathbf Q $ with relatively prime discriminants $ D _ {E} $ and $ D _ {F} $, then $ D _ {EF} = D _ {E} ^ {n} D _ {F} ^ {m} $, where $ n = [ F: \mathbf Q ] $, $ m = [ E: \mathbf Q ] $. This makes it possible to calculate $ D _ {K _ {n} } $ for arbitrary $ n $( see [3]).
For the field $ K _ {p ^ {t} } $, the numbers
$$ \frac{( 1 - \zeta _ {p ^ {t} } ^ {a} ) }{( 1 - \zeta _ {p ^ {t} } ^ {b} ) } , $$
where $ a, b \not\equiv 0 ( \mathop{\rm mod} p) $, generate a subgroup of finite index in the group of all units. The elements of this subgroup are known as circular units or cyclotomic units.
The decomposition law for cyclotomic fields, that is, the law according to which the prime divisors $ ( p) $ in $ \mathbf Q $ factorize into prime divisors in $ K _ {n} $, is a particular case of the general decomposition law in Abelian extensions, established in class field theory (see [4]). Explicitly: If $ ( p, n) = 1 $ and if $ f $ is the least natural number such that $ p ^ {f} \equiv 1 $( $ \mathop{\rm mod} n $), then in $ K _ {n} $,
$$ ( p) = \ \mathfrak p _ {1} \dots \mathfrak p _ {g} , $$
where the prime divisors $ \mathfrak p _ {1} \dots \mathfrak p _ {g} $ are pairwise distinct, $ N ( \mathfrak p _ {i} ) = p ^ {f} $ and $ fg = \phi ( n) $. Thus, the factorization type of $ ( p) $ depends only on the residue of $ p $( $ \mathop{\rm mod} n $). If $ p\mid n $, the exact form of the factorization of $ ( p) $ can be obtained, using the facts that $ K _ {n} = K _ {m} K _ {p ^ {t} } $, where $ ( m, p) = 1 $ and $ ( p) $ is totally ramified in $ K _ {p ^ {t} } $.
If $ K $ is the maximal Abelian extension of $ \mathbf Q $, then $ K = \cup _ {n} K _ {n} $ and
$$ G ( K/ \mathbf Q ) \simeq \ \lim\limits _ \leftarrow G ( K _ {n} / \mathbf Q ) \simeq \ \lim\limits ( \mathbf Z /n \mathbf Z ) ^ {*} \simeq \ \widehat{\mathbf Z} {} ^ {*} , $$
where $ \widehat{\mathbf Z} $ is the completion of the ring of integers $ \mathbf Z $ with respect to all ideals of finite index. In particular, for any prime number $ l $ there is a unique extension $ \mathbf Q _ {\infty , l } / \mathbf Q $ with Galois group isomorphic to the group of $ l $- adic integers $ \mathbf Z _ {l} $.
According to class field theory, there exists a reciprocity map
$$ \psi : J _ {\mathbf Q} \rightarrow \ G ( K/ \mathbf Q ), $$
where $ J _ {\mathbf Q} $ is the idèle group of $ \mathbf Q $. In the case of a cyclotomic field $ \psi $ admits a simple explicit description (see [4]).
Analytic theory.
Many results regarding the structure of the divisor class group of $ K _ {n} $ can be proved by analytic methods. If $ h _ {n} $ is the class number of $ K _ {n} $, then
$$ h _ {n} = \ 2 ^ {-} t \pi ^ {-} t R ^ {-} 1 w \sqrt {| D | } \prod _ {\chi \neq \chi _ {0} } L ( 1, \chi ), $$
here $ w, D $ and $ R $ are, respectively, the number of roots of unity, the discriminant and the regulator of $ K _ {n} $, $ t = \phi ( n)/2 $, and $ L ( 1, \chi ) $ is the Dirichlet $ L $- function for the character $ \chi $, where $ \chi $ runs through all non-trivial primitive multiplicative characters modulo $ n $. The function $ L ( 1, \chi ) $ in turn can be expressed explicitly in terms of Gauss sums (see [7]). This solves the problem of calculating $ h _ {n} $, given $ n $.
There is a natural decomposition of $ h _ {n} $ into two factors, $ h _ {n} = h _ {n} ^ {-} h _ {n} ^ {+} $; the first and second factor of the class number, where $ h _ {n} ^ {+} $ is interpreted as the class number of the field $ K _ {n} ^ {+} $. If $ n = p ^ {t} $ then $ h _ {n} ^ {+} = [ E : E _ {0} ] $, where $ E $ is the group of units of $ K _ {p ^ {t} } ^ {+} $ and $ E _ {0} $ is the group of real cyclotomic units (any cyclotomic unit becomes real if multiplied by a suitable root of unity).
In questions related to the Fermat problem, an important role is played by the divisibility of the class number of $ K _ {l} $ by $ l $, where $ l $ is prime. It is known that $ h _ {l} \equiv 0 $( $ \mathop{\rm mod} l $) for infinitely many prime numbers $ l $( such numbers $ l $ are said to be irregular). As to the set of regular prime numbers $ l $, i.e. numbers for which $ h _ {l} \not\equiv 0 $( $ \mathop{\rm mod} l $), it is not known (1982) whether it is finite or infinite. It has been conjectured that $ h _ {l} ^ {+} \not\equiv 0 $( $ \mathop{\rm mod} l $) for all $ l $, and this has been confirmed in a large number of cases. The factor $ h _ {l} ^ {-} $ is more amenable to investigation. There exists a relatively simple criterion for the divisibility of $ h _ {l} ^ {-} $( and $ h _ {l} $) by $ l $ in terms of Bernoulli numbers ([7]). It is known that $ h _ {l} ^ {-} \rightarrow \infty $ as $ l \rightarrow \infty $ and that $ h _ {l} = 1 $ if and only if $ l \leq 19 $( see [6]).
The so-called $ p $- adic $ L $- functions have been successfully applied to the study of the class groups of cyclotomic fields (see [5], [8]).
References
| [1] | E. Kummer, "Ueber die Zerlegung der aus Wurzeln der Einheit gebildeten komplexen Zahlen in ihre Primfaktoren" J. Reine Angew. Math. , 35 (1847) pp. 327–367 |
| [2] | H. Weyl, "Algebraic theory of numbers" , Princeton Univ. Press (1959) MR1617068 MR0002354 Zbl 0921.11001 Zbl 0063.08223 Zbl 0054.02002 Zbl 66.1210.02 |
| [3] | S. Lang, "Algebraic number theory" , Addison-Wesley (1970) MR0282947 Zbl 0211.38404 |
| [4] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1967) MR0215665 Zbl 0153.07403 |
| [5] | I.R. Shafarevich, "The zeta-function" , Moscow (1969) (In Russian) |
| [6] | K. Uchida, "Class numbers of imaginary abelian number fields III" Tôhoku Math. J. , 23 (1971) pp. 573–580 MR0288097 Zbl 0241.12002 |
| [7] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1975) (Translated from Russian) (German translation: Birkhäuser, 1966) MR1355542 MR1534414 MR0195803 Zbl 0614.00005 Zbl 0592.12001 Zbl 0145.04901 Zbl 0145.04902 Zbl 0121.04202 |
| [8] | K. Iwasawa, "Lectures on 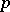 -adic -adic 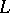 -functions" , Springer (1972) MR360526 -functions" , Springer (1972) MR360526 |
| [9] | S. Lang, "Cyclotomic fields" , Springer (1978) MR0485768 Zbl 0395.12005 |
Comments
It is still not known whether there are infinitely many regular primes (1987), but it is conjectured that the density of the set of regular primes inside the set of all primes is $ e ^ {-} 1/2 \approx 0.6065 $, see [a5]. It has been proved (for $ n \not\equiv 2 $ $ \mathop{\rm mod} 4 $) that $ h _ {n} = 1 $ if and only if $ \phi ( n) \leq 20 $ or $ n = 35, 45 $ or $ 84 $, see [a3], [a5]. An important theorem that describes the structure of the class groups of cyclotomic fields in terms of $ p $- adic $ L $- functions has been proved by B. Mazur and A. Wiles (see [a1], [a4]) with the help of methods from algebraic geometry.
References
| [a1] | J. Coates, "The work of Mazur and Wiles on cyclotomic fields." Sem. Bourbaki , 33 : 575 (1980/81) Lecture Notes in Math. , 901 (1981) pp. 220–242 MR0647499 Zbl 0506.12001 |
| [a2] | S. Lang, "Cyclotomic fields" , II , Springer (1980) MR0566952 Zbl 0435.12001 |
| [a3] | J.M. Masley, H.L. Montgomery, "Cyclotomic fields with unique factorization" J. Reine Angew. Math. , 286–287 (1976) pp. 248–256 MR0429824 Zbl 0335.12013 |
| [a4] | B. Mazur, A. Wiles, "Class fields of abelian extensions of 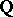 " Invent. Math. , 76 (1984) pp. 179–330 MR0742853 Zbl 0545.12005 " Invent. Math. , 76 (1984) pp. 179–330 MR0742853 Zbl 0545.12005 |
| [a5] | L.C. Washington, "Cyclotomic fields" , Springer (1982) MR0718674 Zbl 0502.12003 Zbl 0484.12001 |
Cyclotomic field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cyclotomic_field&oldid=39901