Covering
A mapping  of a space
of a space  onto a space
onto a space  such that each point
such that each point  has a neighbourhood
has a neighbourhood  the pre-image of which under
the pre-image of which under  is a union of open subsets that are mapped homeomorphically onto
is a union of open subsets that are mapped homeomorphically onto  by
by  . Equivalently:
. Equivalently:  is a locally trivial fibre bundle with discrete fibre.
is a locally trivial fibre bundle with discrete fibre.
Coverings are usually considered on the assumption that 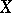 and
and 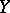 are connected; it is also usually assumed that
are connected; it is also usually assumed that  is locally connected and locally simply-connected. Under these assumptions one can establish a relationship between the fundamental groups
is locally connected and locally simply-connected. Under these assumptions one can establish a relationship between the fundamental groups 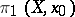 and
and  : If
: If  , then the induced homomorphism
, then the induced homomorphism 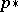 maps
maps 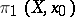 isomorphically onto a subgroup of
isomorphically onto a subgroup of 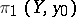 and, by varying the point
and, by varying the point 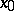 in
in 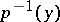 , one obtains exactly all subgroups in the corresponding class of conjugate subgroups. If this class consists of a single subgroup
, one obtains exactly all subgroups in the corresponding class of conjugate subgroups. If this class consists of a single subgroup 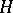 (i.e. if
(i.e. if 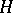 is a normal divisor), the covering is said to be regular. In that case one obtains a free action of the group
is a normal divisor), the covering is said to be regular. In that case one obtains a free action of the group 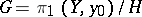 on
on 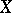 , with
, with 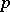 playing the role of the quotient mapping onto the orbit space
playing the role of the quotient mapping onto the orbit space 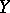 . This action is generated by lifting loops: If one associates with a loop
. This action is generated by lifting loops: If one associates with a loop 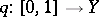 ,
, 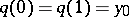 , the unique path
, the unique path 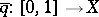 such that
such that 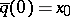 and
and 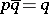 , then the point
, then the point 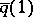 will depend only on the class of the loop in
will depend only on the class of the loop in 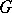 and on
and on 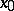 . Thus, each element of
. Thus, each element of  corresponds to a permutation of points in
corresponds to a permutation of points in  . This permutation has no fixed points if
. This permutation has no fixed points if 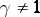 , and it depends continuously on
, and it depends continuously on 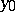 . One obtains a homeomorphism of
. One obtains a homeomorphism of 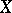 .
.
In the general case this construction defines only a permutation in 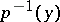 , i.e. there is an action of
, i.e. there is an action of  on
on 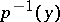 , known as the monodromy of the covering. A special case of a regular covering is a universal covering, for which
, known as the monodromy of the covering. A special case of a regular covering is a universal covering, for which 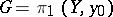 . In general, given any subgroup
. In general, given any subgroup  , one can construct a unique covering
, one can construct a unique covering 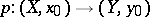 for which
for which 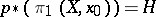 . The points of
. The points of 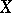 are the classes of paths
are the classes of paths 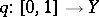 ,
, 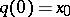 : Two paths
: Two paths 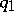 and
and 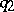 are identified if
are identified if 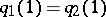 and if the loop
and if the loop  lies in an element of
lies in an element of  . The point
. The point 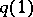 for the paths of one class is taken as the image of this class; this defines
for the paths of one class is taken as the image of this class; this defines 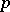 . The topology in
. The topology in 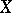 is uniquely determined by the condition that
is uniquely determined by the condition that 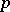 be a covering; it is here that the local simple-connectedness of
be a covering; it is here that the local simple-connectedness of 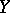 is essential. For any mapping
is essential. For any mapping 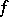 of an arcwise-connected space
of an arcwise-connected space 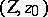 into
into 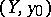 , its lifting into a mapping
, its lifting into a mapping 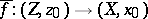 exists if and only if
exists if and only if 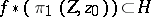 . A partial order relation can be defined on the coverings of
. A partial order relation can be defined on the coverings of 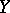 (a covering of a covering is a covering); this relation is dual to the inclusion of subgroups in
(a covering of a covering is a covering); this relation is dual to the inclusion of subgroups in 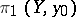 . In particular, the universal covering is the unique maximal element.
. In particular, the universal covering is the unique maximal element.
Examples. The parametrization 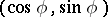 of the circle defines a covering of the circle by the real line,
of the circle defines a covering of the circle by the real line, 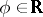 , often described in the complex form
, often described in the complex form 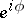 and called the exponential covering. Similarly, the torus is covered by the plane. Identification of antipodal points on a sphere yields a covering by the sphere of a projective space of corresponding dimension. In general, free actions of discrete groups are a source of regular coverings (over the orbit space); not every such action yields a covering (the orbit space may be non-separable), but finite groups do.
and called the exponential covering. Similarly, the torus is covered by the plane. Identification of antipodal points on a sphere yields a covering by the sphere of a projective space of corresponding dimension. In general, free actions of discrete groups are a source of regular coverings (over the orbit space); not every such action yields a covering (the orbit space may be non-separable), but finite groups do.
Comments
A covering is also a termed a covering projection. Every covering has the homotopy lifting property (cf. Covering homotopy) and hence is a Hurewicz fibre space or fibration.
References
| [a1] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) pp. Chapt. 2 |
Covering. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Covering&oldid=13627