Courant-Friedrichs-Lewy condition
A necessary condition for the stability of difference schemes in the class of infinitely-differentiable coefficients. Let  be the dependence region for the value of the solution with respect to one of the coefficients (in particular, the latter might be an initial condition) and let
be the dependence region for the value of the solution with respect to one of the coefficients (in particular, the latter might be an initial condition) and let 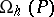 be the dependence region of the value
be the dependence region of the value  of the solution to the corresponding difference equation. A necessary condition for
of the solution to the corresponding difference equation. A necessary condition for 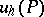 to be convergent to
to be convergent to 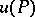 is that, as the grid spacing
is that, as the grid spacing 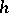 is diminished, the dependence region of the difference equation covers the dependence region of the differential equation, in the sense that
is diminished, the dependence region of the difference equation covers the dependence region of the differential equation, in the sense that
 |
References
| [1] | R. Courant, K.O. Friedrichs, H. Lewy, "Ueber die partiellen Differenzgleichungen der mathematische Physik" Math Ann. , 100 (1928) pp. 32–74 |
| [2] | S.K. Godunov, V.S. Ryaben'kii, "The theory of difference schemes" , North-Holland (1964) (Translated from Russian) |
Comments
The Courant–Friedrichs–Lewy condition is essential for the convergence and stability of explicit difference schemes for hyperbolic equations cf. [a1]–[a5]. Reference [a2] is the translation of [1] into English.
References
| [a1] | R. Courant, K.O. Friedrichs, "Supersonic flow and shock waves" , Interscience (1948) |
| [a2] | R. Courant, K.O. Friedrichs, H. Lewy, "On the partial difference equations of mathematical physics" , NYO-7689 , Inst. Math. Sci. New York Univ. (1956) (Translated from German) |
| [a3] | G.E. Forsythe, W.R. Wasow, "Finite difference methods for partial differential equations" , Wiley (1960) |
| [a4] | A.R. Mitchell, D.F. Griffiths, "The finite difference method in partial equations" , Wiley (1980) |
| [a5] | R.D. Richtmeyer, K.W. Morton, "Difference methods for initial value problems" , Wiley (1967) |
Courant-Friedrichs-Lewy condition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Courant-Friedrichs-Lewy_condition&oldid=22307