Difference between revisions of "Correlation inequalities"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | c1104201.png | ||
| + | $#A+1 = 209 n = 1 | ||
| + | $#C+1 = 209 : ~/encyclopedia/old_files/data/C110/C.1100420 Correlation inequalities | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | As general definitions, one says with respect to a probability measure | + | {{TEX|auto}} |
| + | {{TEX|done}} | ||
| + | |||
| + | [[Correlation|Correlation]] between variables in multivariate statistics (cf. also [[Multi-dimensional statistical analysis|Multi-dimensional statistical analysis]]) [[#References|[a19]]] has motivated classes of inequalities on subsets of a base set $ S $ | ||
| + | that are referred to as correlation inequalities. They are often stated deterministically but usually have probabilistic interpretations. For example, suppose $ S $ | ||
| + | is the family of all subsets of a finite set $ \{ 1 \dots n \} $, | ||
| + | and let $ A $ | ||
| + | and $ B $ | ||
| + | be order ideals or down-sets in $ ( S, \subset ) $: | ||
| + | $ a \subset b \in A $ | ||
| + | implies $ a \in A $, | ||
| + | $ a \subset b \in B $ | ||
| + | implies $ a \in B $, | ||
| + | with $ A, B \subseteq S $. | ||
| + | Then, [[#References|[a13]]], [[#References|[a16]]], $ 2 ^ {n} | {A \cap B } | \geq | A | \cdot | B | $. | ||
| + | When $ \mu $ | ||
| + | is the uniform probability measure (cf. also [[Probability measure|Probability measure]]) on $ 2 ^ {S} $, | ||
| + | so that $ \mu ( a ) = \mu ( \{ a \} ) = 2 ^ {- n } $ | ||
| + | for every $ a \in S $, | ||
| + | and $ \mu ( A ) = | A | 2 ^ {- n } $, | ||
| + | one has $ \mu ( A \cap B ) \geq \mu ( A ) \mu ( B ) $. | ||
| + | Hence, with respect to $ \mu $, | ||
| + | $ A $ | ||
| + | and $ B $ | ||
| + | are correlated whenever both are down-sets. | ||
| + | |||
| + | As general definitions, one says with respect to a probability measure $ \mu $ | ||
| + | on an algebra $ {\mathcal E} $ | ||
| + | of subsets of $ S $ | ||
| + | that $ A, B \in {\mathcal E} $ | ||
| + | are positively correlated if $ \mu ( A \cap B ) > \mu ( A ) \mu ( B ) $ | ||
| + | and non-negatively correlated if $ \mu ( A \cap B ) \geq \mu ( A ) \mu ( B ) $. | ||
| + | Inequality reversals define negative correlation and non-positive correlation, respectively. The instances of these inequalities and generalizations described below assume that $ S $ | ||
| + | is a finite set partially ordered by $ \prec $ | ||
| + | so that $ \prec $ | ||
| + | is irreflexive (never $ a \prec a $) | ||
| + | and transitive: $ a \prec b $ | ||
| + | and $ b \prec c $ | ||
| + | imply $ a \prec c $. | ||
==Inequalities for distributive lattices.== | ==Inequalities for distributive lattices.== | ||
| − | Let | + | Let $ ( S, \prec ) $ |
| + | be a [[Distributive lattice|distributive lattice]] with join $ a \lor b $ | ||
| + | and meet $ a \wedge b $ | ||
| + | defined by | ||
| − | + | $$ | |
| + | a \lor b = \min \left \{ {z \in S } : {a \cle z, b \cle z } \right \} , | ||
| + | $$ | ||
| − | + | $$ | |
| + | a \wedge b = \max \left \{ {z \in S } : {z \cle a, z \cle b } \right \} . | ||
| + | $$ | ||
| − | Distributivity says that | + | Distributivity says that $ a \wedge ( b \lor c ) = ( a \wedge b ) \lor ( a \wedge c ) $ |
| + | for all $ a,b,c \in S $. | ||
| + | A mapping $ f : S \rightarrow \mathbf R $ | ||
| + | is non-decreasing if $ a \prec b $ | ||
| + | implies $ f ( a ) \leq f ( b ) $ | ||
| + | for all $ a,b \in S $, | ||
| + | and $ f ( A ) $ | ||
| + | is defined as $ \sum _ {a \in A } f ( a ) $ | ||
| + | for $ A \subseteq S $, | ||
| + | with $ f ( \emptyset ) = 0 $. | ||
| + | The join and meet $ \lor $ | ||
| + | and $ \wedge $ | ||
| + | can be extended to subsets $ A, B \subseteq S $ | ||
| + | by | ||
| − | + | $$ | |
| + | A \lor B = \left \{ {a \lor b } : {a \in A, b \in B } \right \} , | ||
| + | $$ | ||
| − | + | $$ | |
| + | A \wedge B = \left \{ {a \wedge b } : {a \in A, b \in B } \right \} , | ||
| + | $$ | ||
| − | with the understanding that | + | with the understanding that $ A \lor B = A \wedge B = \emptyset $ |
| + | if $ A $ | ||
| + | or $ B $ | ||
| + | is empty. | ||
| − | The pre-eminent correlation inequality is the [[Ahlswede–Daykin inequality|Ahlswede–Daykin inequality]] [[#References|[a1]]], also called the four-functions inequality [[#References|[a2]]]. It says that if | + | The pre-eminent correlation inequality is the [[Ahlswede–Daykin inequality|Ahlswede–Daykin inequality]] [[#References|[a1]]], also called the four-functions inequality [[#References|[a2]]]. It says that if $ {f _ {1} , f _ {2} , f _ {3} , f _ {4} } : S \rightarrow {[ 0, \infty ) } $ |
| + | satisfy | ||
| − | + | $$ | |
| + | f _ {1} ( a ) f _ {2} ( b ) \leq f _ {3} ( a \lor b ) f _ {4} ( a \wedge b ) \textrm{ for all } a, b \in S, | ||
| + | $$ | ||
then | then | ||
| − | + | $$ | |
| + | f _ {1} ( A ) f _ {2} ( B ) \leq f _ {3} ( A \lor B ) f _ {4} ( A \wedge B ) \textrm{ for all } A, B \subseteq S . | ||
| + | $$ | ||
| − | This is a very powerful result that allows efficient proofs of many other correlation inequalities [[#References|[a2]]], [[#References|[a7]]], [[#References|[a10]]], [[#References|[a23]]]. One unusual application [[#References|[a8]]] concerns match sets of orders of a deck of | + | This is a very powerful result that allows efficient proofs of many other correlation inequalities [[#References|[a2]]], [[#References|[a7]]], [[#References|[a10]]], [[#References|[a23]]]. One unusual application [[#References|[a8]]] concerns match sets of orders of a deck of $ 52 $ |
| + | cards numbered $ 1 $ | ||
| + | through $ 52 $. | ||
| + | For each order, $ M = \{ k : {\textrm{ card } k \textrm{ is the } k \textrm{ th card at the top of the deck } } \} $. | ||
| + | Let $ A = \{ M : {\textrm{ an even } k \in M } \} $ | ||
| + | and $ B = \{ M : {\textrm{ an odd } k \in M } \} $. | ||
| + | When $ \mu $ | ||
| + | is the uniform distribution on the $ 52! $ | ||
| + | orders, $ \mu ( A \cap B ) \geq \mu ( A ) \mu ( B ) $. | ||
| + | Hence, if the match set of a well-shuffled deck contains an odd number, this can only increase our confidence that it contains an even number. | ||
| − | The most important correlation inequality historically is the [[FKG inequality|FKG inequality]] [[#References|[a9]]] (also known as the Fortuin–Kasteleyn–Ginibre inequality), which says that if | + | The most important correlation inequality historically is the [[FKG inequality|FKG inequality]] [[#References|[a9]]] (also known as the Fortuin–Kasteleyn–Ginibre inequality), which says that if $ \eta : S \rightarrow {[ 0, \infty ) } $ |
| + | is log supermodular, i.e., | ||
| − | + | $$ | |
| + | \eta ( a ) \eta ( b ) \leq \eta ( a \lor b ) \eta ( a \wedge b ) \textrm{ for all } a,b \in S, | ||
| + | $$ | ||
| − | and if | + | and if $ f : S \rightarrow \mathbf R $ |
| + | and $ g : S \rightarrow \mathbf R $ | ||
| + | are non-decreasing, then | ||
| − | + | $$ | |
| + | \left [ \sum _ { S } \eta ( a ) f ( a ) \right ] \left [ \sum _ { S } \eta ( a ) g ( a ) \right ] \leq | ||
| + | $$ | ||
| − | + | $$ | |
| + | \leq | ||
| + | \left [ \sum _ { S } \eta ( a ) \right ] \left [ \sum _ { S } \eta ( a ) f ( a ) g ( a ) \right ] . | ||
| + | $$ | ||
| − | This can be written in terms of the [[Mathematical expectation|mathematical expectation]] operation | + | This can be written in terms of the [[Mathematical expectation|mathematical expectation]] operation $ {\mathsf E} _ \eta $ |
| + | as $ {\mathsf E} _ \eta ( f ) {\mathsf E} _ \eta ( g ) \leq {\mathsf E} _ \eta ( fg ) $, | ||
| + | when $ S $ | ||
| + | is a [[Boolean algebra|Boolean algebra]] and $ \eta $ | ||
| + | is a log supermodular [[Probability measure|probability measure]] with $ \lor = \cup $ | ||
| + | and $ \wedge = \cap $. | ||
| + | Suitable definitions of $ f $ | ||
| + | and $ g $ | ||
| + | with $ \{ 0,1 \} $ | ||
| + | co-domains show that $ A, B \subseteq S $ | ||
| + | are non-negatively correlated when both are up-sets or order filters, given log supermodularity. | ||
| − | Another notable result is the [[Holley inequality|Holley inequality]] [[#References|[a12]]]. Suppose | + | Another notable result is the [[Holley inequality|Holley inequality]] [[#References|[a12]]]. Suppose $ {\eta _ {1} } : S \rightarrow {[ 0, \infty ) } $ |
| + | and $ {\eta _ {2} } : S \rightarrow {[ 0, \infty ) } $ | ||
| + | satisfy $ \sum _ {S} \eta _ {1} ( a ) = \sum _ {S} \eta _ {2} ( a ) $ | ||
| + | along with the following inequality that generalizes log supermodularity and is itself generalized by the four-function Ahlswede–Daykin hypothesis: | ||
| − | + | $$ | |
| + | \eta _ {1} ( a ) \eta _ {2} ( b ) \leq \eta _ {1} ( a \lor b ) \eta _ {2} ( a \wedge b ) \textrm{ for all } a,b \in S . | ||
| + | $$ | ||
| − | Then the Holley inequality says that for every non-decreasing | + | Then the Holley inequality says that for every non-decreasing $ f : S \rightarrow \mathbf R $, |
| − | + | $$ | |
| + | \sum _ { S } f ( a ) \eta _ {1} ( a ) \geq \sum _ { S } f ( a ) \eta _ {2} ( a ) . | ||
| + | $$ | ||
| − | Simple proofs of the FKG and Holley inequalities follow from the Ahlswede–Daykin inequality by suitable choices of | + | Simple proofs of the FKG and Holley inequalities follow from the Ahlswede–Daykin inequality by suitable choices of $ f _ {1} $ |
| + | through $ f _ {4} $. | ||
| + | Also, when $ f _ {i} = \eta $ | ||
| + | for all $ i $, | ||
| + | log supermodularity on $ S $ | ||
| + | implies log supermodularity on the subsets of $ S $; | ||
| + | when $ f _ {i} \equiv 1 $ | ||
| + | for all $ i $, | ||
| + | one obtains $ | A | \cdot | B | \leq | {A \lor B } | \cdot | {A \wedge B } | $ | ||
| + | for all $ A,B \subseteq S $, | ||
| + | which is equivalent to distributivity [[#References|[a5]]] for an ordered lattice $ ( S, \prec ) $. | ||
==Systems of subsets.== | ==Systems of subsets.== | ||
| − | Several inequalities for | + | Several inequalities for $ ( S, \subset ) $ |
| + | when $ S $ | ||
| + | is the family of subsets of $ \{ 1 \dots n \} $ | ||
| + | have already been given. Log supermodularity for a probability measure $ \mu $ | ||
| + | on $ 2 ^ {S} $ | ||
| + | is defined as $ \mu ( a ) \mu ( b ) \leq \mu ( a \cup b ) \mu ( a \cap b ) $ | ||
| + | for all $ a,b \in S $, | ||
| + | and when this holds, the FKG inequality says that $ {\mathsf E} _ \mu ( f ) {\mathsf E} _ \mu ( g ) \leq {\mathsf E} _ \mu ( fg ) $ | ||
| + | for non-decreasing $ f : S \rightarrow \mathbf R $ | ||
| + | and $ g : S \rightarrow \mathbf R $ | ||
| + | and implies that $ \mu ( A ) \mu ( B ) \leq \mu ( A \lor B ) \mu ( A \wedge B ) $ | ||
| + | for all $ A,B \subseteq S $. | ||
| + | In addition, if $ A $ | ||
| + | and $ B $ | ||
| + | are down-sets or up-sets, then $ \mu ( A \cap B ) \geq \mu ( A ) \mu ( B ) $. | ||
| + | When $ \mu $ | ||
| + | is uniform, in which case log supermodularity is automatic, $ 2 ^ {n} | {A \cap B } | \leq | A | \cdot | B | $ | ||
| + | if $ A $ | ||
| + | is an up-set and $ B $ | ||
| + | is a down-set, so the two are non-positively correlated when the complementary orientations obtain. | ||
| − | Another inequality involves set differences [[#References|[a14]]]. Let | + | Another inequality involves set differences [[#References|[a14]]]. Let $ A - B = \{ {a \setminus b } : {a \in A, b \in B } \} $ |
| + | for $ A, B \subseteq S $. | ||
| + | Then $ | {A - B } | \cdot | {B - A } | \geq | A | \cdot | B | $, | ||
| + | and, in particular, $ | {A - A } | \geq | A | $. | ||
| − | The match set of a permutation | + | The match set of a permutation $ \sigma $ |
| + | on $ \{ 1 \dots n \} $ | ||
| + | is defined as $ M ( \sigma ) = \{ {i \in \{ 1 \dots n \} } : {\sigma ( i ) = i } \} $. | ||
| + | Assuming that all $ n! $ | ||
| + | permutations are equally likely, let $ \mu ( a ) $ | ||
| + | for $ a \subseteq \{ 1 \dots n \} $ | ||
| + | be the probability that $ M ( \sigma ) = a $. | ||
| + | Note that $ \mu ( a ) = 0 $ | ||
| + | when $ | a | = n - 1 $ | ||
| + | and hence that $ \mu $ | ||
| + | is not log supermodular. However, there still is an FKG-like inequality [[#References|[a8]]], because $ \mu ( A \cap B ) \geq \mu ( A ) \mu ( B ) $ | ||
| + | whenever $ A,B \subseteq S $ | ||
| + | are up-sets. This illustrates the non-necessity of log supermodularity in certain cases for a correlation inequality to hold. | ||
==Linear extensions.== | ==Linear extensions.== | ||
| − | Another class of correlation inequalities arises when | + | Another class of correlation inequalities arises when $ S $ |
| + | is the set of linear extensions of a finite partially ordered set $ ( X, \prec ) $ | ||
| + | and all members of $ S $ | ||
| + | are equally likely. $ ( X, < _ {0} ) $ | ||
| + | is a linear extension of $ ( X, \prec ) $ | ||
| + | if $ ( X, < _ {0} ) $ | ||
| + | is a partially ordered set, $ \prec \subseteq < _ {0} $ | ||
| + | and, for all distinct $ x,y \in X $, | ||
| + | $ x < _ {0} y $ | ||
| + | or $ y < _ {0} x $. | ||
| + | Let $ N $ | ||
| + | be the number of linear extensions of $ ( X, \prec ) $, | ||
| + | so the probability law for $ S $ | ||
| + | is $ \mu ( a ) = 1/N $. | ||
| + | By additivity, $ \mu ( A ) = \sum _ {A} \mu ( a ) $ | ||
| + | for each subset $ A $ | ||
| + | of linear extensions. | ||
| − | A premier correlation inequality in this setting is the [[Fishburn–Shepp inequality|Fishburn–Shepp inequality]] [[#References|[a6]]], [[#References|[a18]]], also known as the | + | A premier correlation inequality in this setting is the [[Fishburn–Shepp inequality|Fishburn–Shepp inequality]] [[#References|[a6]]], [[#References|[a18]]], also known as the $ xyz $ |
| + | inequality. One says that $ x,y \in X $ | ||
| + | are incomparable if $ x \neq y $ | ||
| + | and neither $ x \prec y $ | ||
| + | nor $ y \prec x $, | ||
| + | and denotes by $ ( x _ {1} < _ {0} y _ {1} \dots x _ {m} < _ {0} y _ {m} ) $ | ||
| + | the set of all linear extensions of $ ( X, \prec ) $ | ||
| + | that satisfy the $ x _ {i} < _ {0} y _ {i} $ | ||
| + | relations. The Fishburn–Shepp inequality says that if $ x $, | ||
| + | $ y $ | ||
| + | and $ z $ | ||
| + | are mutually incomparable in $ ( X, \prec ) $, | ||
| + | then | ||
| − | < | + | $$ |
| + | \mu ( x < _ {0} y ) \mu ( x < _ {0} z ) < \mu ( x < _ {0} y, x < _ {0} z ) , | ||
| + | $$ | ||
| − | so events < | + | so events $ A = ( x < _ {0} y ) $ |
| + | and $ B = ( x < _ {0} z ) $ | ||
| + | are positively correlated. Rewritten as $ \mu ( A \cap B ) / \mu ( A ) > \mu ( B ) $, | ||
| + | one sees that the probability of $ x < _ {0} z $ | ||
| + | in a randomly chosen linear extension increases when it is true also that $ x < _ {0} y $. | ||
| + | Examples in [[#References|[a10]]], [[#References|[a17]]], [[#References|[a18]]] show that other plausible positive or non-negative correlations need not be true. | ||
| − | Inequalities involving two-part partitions of | + | Inequalities involving two-part partitions of $ X $ |
| + | are featured in [[#References|[a11]]], [[#References|[a17]]]. Suppose $ \{ X _ {1} , X _ {2} \} $ | ||
| + | is a non-trivial [[Partition|partition]] of $ X $. | ||
| + | Let $ A = ( a _ {1} < _ {0} b _ {1} \dots a _ {j} < _ {0} b _ {j} ) $ | ||
| + | and $ B = ( c _ {1} < _ {0} d _ {1} \dots c _ {k} < _ {0} d _ {k} ) $ | ||
| + | for $ a _ {i} , c _ {i} \in X _ {1} $ | ||
| + | and $ b _ {i} , d _ {i} \in X _ {2} $. | ||
| + | If the restriction of $ \prec $ | ||
| + | in $ ( X, \prec ) $ | ||
| + | to each $ X _ {i} $ | ||
| + | is a linear order (cf. also [[Order (on a set)|Order (on a set)]]), then $ A $ | ||
| + | and $ B $ | ||
| + | are non-negatively correlated, i.e. $ \mu ( A \cap B ) \geq \mu ( A ) \mu ( B ) $. | ||
| + | The same is true if $ \prec = \prec _ {1} \cup \prec _ {2} $, | ||
| + | where $ \prec _ {i} $ | ||
| + | is a partial order on $ X _ {i} $. | ||
| − | Other inequalities which use two ordering relations on a fixed | + | Other inequalities which use two ordering relations on a fixed $ Y \subseteq X $ |
| + | that are associated with $ \prec $ | ||
| + | are in [[#References|[a3]]], [[#References|[a4]]], [[#References|[a7]]], [[#References|[a22]]], [[#References|[a23]]]. One of these, [[#References|[a3]]], shows that the plausible inequality | ||
| − | < | + | $$ |
| + | \mu ( x < _ {0} y < _ {0} z < _ {0} w ) \leq \mu ( x < _ {0} y < _ {0} z ) \mu ( z < _ {0} w ) , | ||
| + | $$ | ||
| − | which is suggested by the non-strict rendering < | + | which is suggested by the non-strict rendering $ \mu ( x < _ {0} y < _ {0} z ) \leq \mu ( x < _ {0} y ) \mu ( y < _ {0} z ) $ |
| + | of the Fishburn–Shepp inequality, can be contradicted whenever $ n \geq 5 $. | ||
==An inequality from percolation theory.== | ==An inequality from percolation theory.== | ||
| − | A final inequality comes from percolation theory [[#References|[a20]]], [[#References|[a21]]] and provides a nice contrast to the FKG inequality version | + | A final inequality comes from percolation theory [[#References|[a20]]], [[#References|[a21]]] and provides a nice contrast to the FKG inequality version $ | A | \cdot | B | \leq 2 ^ {n} | {A \cap B } | $ |
| + | when $ A $ | ||
| + | and $ B $ | ||
| + | are up-sets in the family of subsets of $ \{ 1 \dots n \} $. | ||
| + | For convenience, the subsets of $ \{ 1 \dots n \} $ | ||
| + | are written in characteristic vector form, so that $ S = \{ 0, 1 \} ^ {n} $. | ||
| + | The cylinder set determined by $ x \in S $ | ||
| + | and $ K \subseteq \{ 1 \dots n \} $ | ||
| + | is defined as | ||
| − | + | $$ | |
| + | c ( x, K ) = \left \{ {y \in S } : {y _ {j} = x _ {j} \textrm{ for all } j \in K } \right \} , | ||
| + | $$ | ||
| − | and the disjoint intersection of | + | and the disjoint intersection of $ A, B \subseteq S $ |
| + | is defined by | ||
| − | + | $$ | |
| + | A \square B = \left \{ {x \in S } : c ( x, K ) \subseteq A,\right . | ||
| + | $$ | ||
| − | + | $$ | |
| + | \left . | ||
| + | c ( x, \{ 1 \dots n \} \setminus K ) \subseteq B \textrm{ for some } K \right \} . | ||
| + | $$ | ||
The inequality, conjectured in [[#References|[a20]]], [[#References|[a21]]] and proved in [[#References|[a15]]], is | The inequality, conjectured in [[#References|[a20]]], [[#References|[a21]]] and proved in [[#References|[a15]]], is | ||
| − | + | $$ | |
| + | 2 ^ {n} \left | {A \square B } \right | \leq \left | A \right | \cdot \left | B \right | \textrm{ for all } A, B \subseteq S . | ||
| + | $$ | ||
| − | Thus, whereas some | + | Thus, whereas some $ A, B \subseteq S $ |
| + | are positively correlated by the usual definition based on $ A \cap B $, | ||
| + | all $ A, B \subseteq S $ | ||
| + | are "non-positively correlated" with respect to the disjoint intersection $ A \square B $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Ahlswede, D.E. Daykin, "An inequality for the weights of two families, their unions and intersections" ''Z. Wahrscheinlichkeitsth. verw. Gebiete'' , '''43''' (1978) pp. 183–185</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> B. Bollobás, "Combinatorics" , Cambridge Univ. Press (1986)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> G.R. Brightwell, "Universal correlations in finite posets" ''Order'' , '''2''' (1985) pp. 129–144</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> G.R. Brightwell, "Some correlation inequalities in finite posets" ''Order'' , '''2''' (1986) pp. 387–402</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> D.E. Daykin, "A lattice is distributive if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c110/c110420/c110420211.png" />" ''Nanta Math.'' , '''10''' (1977) pp. 58–60</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> P.C. Fishburn, "A correlational inequality for linear extensions of a poset" ''Order'' , '''1''' (1984) pp. 127–137</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> P.C. Fishburn, "Correlation in partially ordered sets" ''Discrete Appl. Math.'' , '''39''' (1992) pp. 173–191</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> P.C. Fishburn, P.G. Doyle, L.A. Shepp, "The match set of a random permutation has the FKG property" ''Ann. of Probab.'' , '''16''' (1988) pp. 1194–1214</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> C.M. Fortuin, P.N. Kasteleyn, J. Ginibre, "Correlation inequalities for some partially ordered sets" ''Comm. Math. Phys.'' , '''22''' (1971) pp. 89–103</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> R.L. Graham, "Applications of the FKG inequality and its relatives" , ''Proc. 12th Internat. Symp. Math. Programming'' , Springer (1983) pp. 115–131</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> R.L Graham, A.C. Yao, F.F. Yao, "Some monotonicity properties of partial orders" ''SIAM J. Alg. Discrete Methods'' , '''1''' (1980) pp. 251–258</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> R. Holley, "Remarks on the FKG inequalities" ''Comm. Math. Phys.'' , '''36''' (1974) pp. 227–231</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> D.J. Kleitman, "Families of non-disjoint sets" ''J. Combin. Th.'' , '''1''' (1966) pp. 153–155</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> J. Marica, J. Schönheim, "Differences of sets and a problem of Graham" ''Canad. Math. Bull.'' , '''12''' (1969) pp. 635–637</TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> D. Reimer, ''in preparation'' (to appear)</TD></TR><TR><TD valign="top">[a16]</TD> <TD valign="top"> P.D. Seymour, "On incomparable collections of sets" ''Mathematika'' , '''20''' (1973) pp. 208–209</TD></TR><TR><TD valign="top">[a17]</TD> <TD valign="top"> L.A. Shepp, "The FKG property and some monotonicity properties of partial orders" ''SIAM J. Alg. Discrete Methods'' , '''1''' (1980) pp. 295–299</TD></TR><TR><TD valign="top">[a18]</TD> <TD valign="top"> L.A. Shepp, "The XYZ conjecture and the FKG inequality" ''Ann. of Probab.'' , '''10''' (1982) pp. 824–827</TD></TR><TR><TD valign="top">[a19]</TD> <TD valign="top"> R.F. Tate, "Correlation methods" W.H. Kruskal (ed.) J.M. Tanur (ed.) , ''Internat. Encycl. Stat.'' , '''1''' , Free Press (1978) pp. 615–628</TD></TR><TR><TD valign="top">[a20]</TD> <TD valign="top"> J. van der Berg, U. Fiebig, "On a combinatorial conjecture concerning disjoint occurrences of events" ''Ann. of Probab.'' , '''15''' (1987) pp. 354–374</TD></TR><TR><TD valign="top">[a21]</TD> <TD valign="top"> J. van der Berg, H. Kesten, "Inequalities with applications to percolation and reliability" ''J. Appl. Probab.'' , '''22''' (1985) pp. 556–569</TD></TR><TR><TD valign="top">[a22]</TD> <TD valign="top"> P.M. Winkler, "Correlation among partial orders" ''SIAM J. Alg. Discrete Methods'' , '''4''' (1983) pp. 1–7</TD></TR><TR><TD valign="top">[a23]</TD> <TD valign="top"> P M. Winkler, "Correlation and order" ''Contemp. Math.'' , '''57''' (1986) pp. 151–174</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Ahlswede, D.E. Daykin, "An inequality for the weights of two families, their unions and intersections" ''Z. Wahrscheinlichkeitsth. verw. Gebiete'' , '''43''' (1978) pp. 183–185</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> B. Bollobás, "Combinatorics" , Cambridge Univ. Press (1986)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> G.R. Brightwell, "Universal correlations in finite posets" ''Order'' , '''2''' (1985) pp. 129–144</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> G.R. Brightwell, "Some correlation inequalities in finite posets" ''Order'' , '''2''' (1986) pp. 387–402</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> D.E. Daykin, "A lattice is distributive if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c110/c110420/c110420211.png" />" ''Nanta Math.'' , '''10''' (1977) pp. 58–60</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> P.C. Fishburn, "A correlational inequality for linear extensions of a poset" ''Order'' , '''1''' (1984) pp. 127–137</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> P.C. Fishburn, "Correlation in partially ordered sets" ''Discrete Appl. Math.'' , '''39''' (1992) pp. 173–191</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> P.C. Fishburn, P.G. Doyle, L.A. Shepp, "The match set of a random permutation has the FKG property" ''Ann. of Probab.'' , '''16''' (1988) pp. 1194–1214</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> C.M. Fortuin, P.N. Kasteleyn, J. Ginibre, "Correlation inequalities for some partially ordered sets" ''Comm. Math. Phys.'' , '''22''' (1971) pp. 89–103</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> R.L. Graham, "Applications of the FKG inequality and its relatives" , ''Proc. 12th Internat. Symp. Math. Programming'' , Springer (1983) pp. 115–131</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> R.L Graham, A.C. Yao, F.F. Yao, "Some monotonicity properties of partial orders" ''SIAM J. Alg. Discrete Methods'' , '''1''' (1980) pp. 251–258</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> R. Holley, "Remarks on the FKG inequalities" ''Comm. Math. Phys.'' , '''36''' (1974) pp. 227–231</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> D.J. Kleitman, "Families of non-disjoint sets" ''J. Combin. Th.'' , '''1''' (1966) pp. 153–155</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> J. Marica, J. Schönheim, "Differences of sets and a problem of Graham" ''Canad. Math. Bull.'' , '''12''' (1969) pp. 635–637</TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> D. Reimer, ''in preparation'' (to appear)</TD></TR><TR><TD valign="top">[a16]</TD> <TD valign="top"> P.D. Seymour, "On incomparable collections of sets" ''Mathematika'' , '''20''' (1973) pp. 208–209</TD></TR><TR><TD valign="top">[a17]</TD> <TD valign="top"> L.A. Shepp, "The FKG property and some monotonicity properties of partial orders" ''SIAM J. Alg. Discrete Methods'' , '''1''' (1980) pp. 295–299</TD></TR><TR><TD valign="top">[a18]</TD> <TD valign="top"> L.A. Shepp, "The XYZ conjecture and the FKG inequality" ''Ann. of Probab.'' , '''10''' (1982) pp. 824–827</TD></TR><TR><TD valign="top">[a19]</TD> <TD valign="top"> R.F. Tate, "Correlation methods" W.H. Kruskal (ed.) J.M. Tanur (ed.) , ''Internat. Encycl. Stat.'' , '''1''' , Free Press (1978) pp. 615–628</TD></TR><TR><TD valign="top">[a20]</TD> <TD valign="top"> J. van der Berg, U. Fiebig, "On a combinatorial conjecture concerning disjoint occurrences of events" ''Ann. of Probab.'' , '''15''' (1987) pp. 354–374</TD></TR><TR><TD valign="top">[a21]</TD> <TD valign="top"> J. van der Berg, H. Kesten, "Inequalities with applications to percolation and reliability" ''J. Appl. Probab.'' , '''22''' (1985) pp. 556–569</TD></TR><TR><TD valign="top">[a22]</TD> <TD valign="top"> P.M. Winkler, "Correlation among partial orders" ''SIAM J. Alg. Discrete Methods'' , '''4''' (1983) pp. 1–7</TD></TR><TR><TD valign="top">[a23]</TD> <TD valign="top"> P M. Winkler, "Correlation and order" ''Contemp. Math.'' , '''57''' (1986) pp. 151–174</TD></TR></table> | ||
Revision as of 17:31, 5 June 2020
Correlation between variables in multivariate statistics (cf. also Multi-dimensional statistical analysis) [a19] has motivated classes of inequalities on subsets of a base set $ S $
that are referred to as correlation inequalities. They are often stated deterministically but usually have probabilistic interpretations. For example, suppose $ S $
is the family of all subsets of a finite set $ \{ 1 \dots n \} $,
and let $ A $
and $ B $
be order ideals or down-sets in $ ( S, \subset ) $:
$ a \subset b \in A $
implies $ a \in A $,
$ a \subset b \in B $
implies $ a \in B $,
with $ A, B \subseteq S $.
Then, [a13], [a16], $ 2 ^ {n} | {A \cap B } | \geq | A | \cdot | B | $.
When $ \mu $
is the uniform probability measure (cf. also Probability measure) on $ 2 ^ {S} $,
so that $ \mu ( a ) = \mu ( \{ a \} ) = 2 ^ {- n } $
for every $ a \in S $,
and $ \mu ( A ) = | A | 2 ^ {- n } $,
one has $ \mu ( A \cap B ) \geq \mu ( A ) \mu ( B ) $.
Hence, with respect to $ \mu $,
$ A $
and $ B $
are correlated whenever both are down-sets.
As general definitions, one says with respect to a probability measure $ \mu $ on an algebra $ {\mathcal E} $ of subsets of $ S $ that $ A, B \in {\mathcal E} $ are positively correlated if $ \mu ( A \cap B ) > \mu ( A ) \mu ( B ) $ and non-negatively correlated if $ \mu ( A \cap B ) \geq \mu ( A ) \mu ( B ) $. Inequality reversals define negative correlation and non-positive correlation, respectively. The instances of these inequalities and generalizations described below assume that $ S $ is a finite set partially ordered by $ \prec $ so that $ \prec $ is irreflexive (never $ a \prec a $) and transitive: $ a \prec b $ and $ b \prec c $ imply $ a \prec c $.
Inequalities for distributive lattices.
Let $ ( S, \prec ) $ be a distributive lattice with join $ a \lor b $ and meet $ a \wedge b $ defined by
$$ a \lor b = \min \left \{ {z \in S } : {a \cle z, b \cle z } \right \} , $$
$$ a \wedge b = \max \left \{ {z \in S } : {z \cle a, z \cle b } \right \} . $$
Distributivity says that $ a \wedge ( b \lor c ) = ( a \wedge b ) \lor ( a \wedge c ) $ for all $ a,b,c \in S $. A mapping $ f : S \rightarrow \mathbf R $ is non-decreasing if $ a \prec b $ implies $ f ( a ) \leq f ( b ) $ for all $ a,b \in S $, and $ f ( A ) $ is defined as $ \sum _ {a \in A } f ( a ) $ for $ A \subseteq S $, with $ f ( \emptyset ) = 0 $. The join and meet $ \lor $ and $ \wedge $ can be extended to subsets $ A, B \subseteq S $ by
$$ A \lor B = \left \{ {a \lor b } : {a \in A, b \in B } \right \} , $$
$$ A \wedge B = \left \{ {a \wedge b } : {a \in A, b \in B } \right \} , $$
with the understanding that $ A \lor B = A \wedge B = \emptyset $ if $ A $ or $ B $ is empty.
The pre-eminent correlation inequality is the Ahlswede–Daykin inequality [a1], also called the four-functions inequality [a2]. It says that if $ {f _ {1} , f _ {2} , f _ {3} , f _ {4} } : S \rightarrow {[ 0, \infty ) } $ satisfy
$$ f _ {1} ( a ) f _ {2} ( b ) \leq f _ {3} ( a \lor b ) f _ {4} ( a \wedge b ) \textrm{ for all } a, b \in S, $$
then
$$ f _ {1} ( A ) f _ {2} ( B ) \leq f _ {3} ( A \lor B ) f _ {4} ( A \wedge B ) \textrm{ for all } A, B \subseteq S . $$
This is a very powerful result that allows efficient proofs of many other correlation inequalities [a2], [a7], [a10], [a23]. One unusual application [a8] concerns match sets of orders of a deck of $ 52 $ cards numbered $ 1 $ through $ 52 $. For each order, $ M = \{ k : {\textrm{ card } k \textrm{ is the } k \textrm{ th card at the top of the deck } } \} $. Let $ A = \{ M : {\textrm{ an even } k \in M } \} $ and $ B = \{ M : {\textrm{ an odd } k \in M } \} $. When $ \mu $ is the uniform distribution on the $ 52! $ orders, $ \mu ( A \cap B ) \geq \mu ( A ) \mu ( B ) $. Hence, if the match set of a well-shuffled deck contains an odd number, this can only increase our confidence that it contains an even number.
The most important correlation inequality historically is the FKG inequality [a9] (also known as the Fortuin–Kasteleyn–Ginibre inequality), which says that if $ \eta : S \rightarrow {[ 0, \infty ) } $ is log supermodular, i.e.,
$$ \eta ( a ) \eta ( b ) \leq \eta ( a \lor b ) \eta ( a \wedge b ) \textrm{ for all } a,b \in S, $$
and if $ f : S \rightarrow \mathbf R $ and $ g : S \rightarrow \mathbf R $ are non-decreasing, then
$$ \left [ \sum _ { S } \eta ( a ) f ( a ) \right ] \left [ \sum _ { S } \eta ( a ) g ( a ) \right ] \leq $$
$$ \leq \left [ \sum _ { S } \eta ( a ) \right ] \left [ \sum _ { S } \eta ( a ) f ( a ) g ( a ) \right ] . $$
This can be written in terms of the mathematical expectation operation $ {\mathsf E} _ \eta $ as $ {\mathsf E} _ \eta ( f ) {\mathsf E} _ \eta ( g ) \leq {\mathsf E} _ \eta ( fg ) $, when $ S $ is a Boolean algebra and $ \eta $ is a log supermodular probability measure with $ \lor = \cup $ and $ \wedge = \cap $. Suitable definitions of $ f $ and $ g $ with $ \{ 0,1 \} $ co-domains show that $ A, B \subseteq S $ are non-negatively correlated when both are up-sets or order filters, given log supermodularity.
Another notable result is the Holley inequality [a12]. Suppose $ {\eta _ {1} } : S \rightarrow {[ 0, \infty ) } $ and $ {\eta _ {2} } : S \rightarrow {[ 0, \infty ) } $ satisfy $ \sum _ {S} \eta _ {1} ( a ) = \sum _ {S} \eta _ {2} ( a ) $ along with the following inequality that generalizes log supermodularity and is itself generalized by the four-function Ahlswede–Daykin hypothesis:
$$ \eta _ {1} ( a ) \eta _ {2} ( b ) \leq \eta _ {1} ( a \lor b ) \eta _ {2} ( a \wedge b ) \textrm{ for all } a,b \in S . $$
Then the Holley inequality says that for every non-decreasing $ f : S \rightarrow \mathbf R $,
$$ \sum _ { S } f ( a ) \eta _ {1} ( a ) \geq \sum _ { S } f ( a ) \eta _ {2} ( a ) . $$
Simple proofs of the FKG and Holley inequalities follow from the Ahlswede–Daykin inequality by suitable choices of $ f _ {1} $ through $ f _ {4} $. Also, when $ f _ {i} = \eta $ for all $ i $, log supermodularity on $ S $ implies log supermodularity on the subsets of $ S $; when $ f _ {i} \equiv 1 $ for all $ i $, one obtains $ | A | \cdot | B | \leq | {A \lor B } | \cdot | {A \wedge B } | $ for all $ A,B \subseteq S $, which is equivalent to distributivity [a5] for an ordered lattice $ ( S, \prec ) $.
Systems of subsets.
Several inequalities for $ ( S, \subset ) $ when $ S $ is the family of subsets of $ \{ 1 \dots n \} $ have already been given. Log supermodularity for a probability measure $ \mu $ on $ 2 ^ {S} $ is defined as $ \mu ( a ) \mu ( b ) \leq \mu ( a \cup b ) \mu ( a \cap b ) $ for all $ a,b \in S $, and when this holds, the FKG inequality says that $ {\mathsf E} _ \mu ( f ) {\mathsf E} _ \mu ( g ) \leq {\mathsf E} _ \mu ( fg ) $ for non-decreasing $ f : S \rightarrow \mathbf R $ and $ g : S \rightarrow \mathbf R $ and implies that $ \mu ( A ) \mu ( B ) \leq \mu ( A \lor B ) \mu ( A \wedge B ) $ for all $ A,B \subseteq S $. In addition, if $ A $ and $ B $ are down-sets or up-sets, then $ \mu ( A \cap B ) \geq \mu ( A ) \mu ( B ) $. When $ \mu $ is uniform, in which case log supermodularity is automatic, $ 2 ^ {n} | {A \cap B } | \leq | A | \cdot | B | $ if $ A $ is an up-set and $ B $ is a down-set, so the two are non-positively correlated when the complementary orientations obtain.
Another inequality involves set differences [a14]. Let $ A - B = \{ {a \setminus b } : {a \in A, b \in B } \} $ for $ A, B \subseteq S $. Then $ | {A - B } | \cdot | {B - A } | \geq | A | \cdot | B | $, and, in particular, $ | {A - A } | \geq | A | $.
The match set of a permutation $ \sigma $ on $ \{ 1 \dots n \} $ is defined as $ M ( \sigma ) = \{ {i \in \{ 1 \dots n \} } : {\sigma ( i ) = i } \} $. Assuming that all $ n! $ permutations are equally likely, let $ \mu ( a ) $ for $ a \subseteq \{ 1 \dots n \} $ be the probability that $ M ( \sigma ) = a $. Note that $ \mu ( a ) = 0 $ when $ | a | = n - 1 $ and hence that $ \mu $ is not log supermodular. However, there still is an FKG-like inequality [a8], because $ \mu ( A \cap B ) \geq \mu ( A ) \mu ( B ) $ whenever $ A,B \subseteq S $ are up-sets. This illustrates the non-necessity of log supermodularity in certain cases for a correlation inequality to hold.
Linear extensions.
Another class of correlation inequalities arises when $ S $ is the set of linear extensions of a finite partially ordered set $ ( X, \prec ) $ and all members of $ S $ are equally likely. $ ( X, < _ {0} ) $ is a linear extension of $ ( X, \prec ) $ if $ ( X, < _ {0} ) $ is a partially ordered set, $ \prec \subseteq < _ {0} $ and, for all distinct $ x,y \in X $, $ x < _ {0} y $ or $ y < _ {0} x $. Let $ N $ be the number of linear extensions of $ ( X, \prec ) $, so the probability law for $ S $ is $ \mu ( a ) = 1/N $. By additivity, $ \mu ( A ) = \sum _ {A} \mu ( a ) $ for each subset $ A $ of linear extensions.
A premier correlation inequality in this setting is the Fishburn–Shepp inequality [a6], [a18], also known as the $ xyz $ inequality. One says that $ x,y \in X $ are incomparable if $ x \neq y $ and neither $ x \prec y $ nor $ y \prec x $, and denotes by $ ( x _ {1} < _ {0} y _ {1} \dots x _ {m} < _ {0} y _ {m} ) $ the set of all linear extensions of $ ( X, \prec ) $ that satisfy the $ x _ {i} < _ {0} y _ {i} $ relations. The Fishburn–Shepp inequality says that if $ x $, $ y $ and $ z $ are mutually incomparable in $ ( X, \prec ) $, then
$$ \mu ( x < _ {0} y ) \mu ( x < _ {0} z ) < \mu ( x < _ {0} y, x < _ {0} z ) , $$
so events $ A = ( x < _ {0} y ) $ and $ B = ( x < _ {0} z ) $ are positively correlated. Rewritten as $ \mu ( A \cap B ) / \mu ( A ) > \mu ( B ) $, one sees that the probability of $ x < _ {0} z $ in a randomly chosen linear extension increases when it is true also that $ x < _ {0} y $. Examples in [a10], [a17], [a18] show that other plausible positive or non-negative correlations need not be true.
Inequalities involving two-part partitions of $ X $ are featured in [a11], [a17]. Suppose $ \{ X _ {1} , X _ {2} \} $ is a non-trivial partition of $ X $. Let $ A = ( a _ {1} < _ {0} b _ {1} \dots a _ {j} < _ {0} b _ {j} ) $ and $ B = ( c _ {1} < _ {0} d _ {1} \dots c _ {k} < _ {0} d _ {k} ) $ for $ a _ {i} , c _ {i} \in X _ {1} $ and $ b _ {i} , d _ {i} \in X _ {2} $. If the restriction of $ \prec $ in $ ( X, \prec ) $ to each $ X _ {i} $ is a linear order (cf. also Order (on a set)), then $ A $ and $ B $ are non-negatively correlated, i.e. $ \mu ( A \cap B ) \geq \mu ( A ) \mu ( B ) $. The same is true if $ \prec = \prec _ {1} \cup \prec _ {2} $, where $ \prec _ {i} $ is a partial order on $ X _ {i} $.
Other inequalities which use two ordering relations on a fixed $ Y \subseteq X $ that are associated with $ \prec $ are in [a3], [a4], [a7], [a22], [a23]. One of these, [a3], shows that the plausible inequality
$$ \mu ( x < _ {0} y < _ {0} z < _ {0} w ) \leq \mu ( x < _ {0} y < _ {0} z ) \mu ( z < _ {0} w ) , $$
which is suggested by the non-strict rendering $ \mu ( x < _ {0} y < _ {0} z ) \leq \mu ( x < _ {0} y ) \mu ( y < _ {0} z ) $ of the Fishburn–Shepp inequality, can be contradicted whenever $ n \geq 5 $.
An inequality from percolation theory.
A final inequality comes from percolation theory [a20], [a21] and provides a nice contrast to the FKG inequality version $ | A | \cdot | B | \leq 2 ^ {n} | {A \cap B } | $ when $ A $ and $ B $ are up-sets in the family of subsets of $ \{ 1 \dots n \} $. For convenience, the subsets of $ \{ 1 \dots n \} $ are written in characteristic vector form, so that $ S = \{ 0, 1 \} ^ {n} $. The cylinder set determined by $ x \in S $ and $ K \subseteq \{ 1 \dots n \} $ is defined as
$$ c ( x, K ) = \left \{ {y \in S } : {y _ {j} = x _ {j} \textrm{ for all } j \in K } \right \} , $$
and the disjoint intersection of $ A, B \subseteq S $ is defined by
$$ A \square B = \left \{ {x \in S } : c ( x, K ) \subseteq A,\right . $$
$$ \left . c ( x, \{ 1 \dots n \} \setminus K ) \subseteq B \textrm{ for some } K \right \} . $$
The inequality, conjectured in [a20], [a21] and proved in [a15], is
$$ 2 ^ {n} \left | {A \square B } \right | \leq \left | A \right | \cdot \left | B \right | \textrm{ for all } A, B \subseteq S . $$
Thus, whereas some $ A, B \subseteq S $ are positively correlated by the usual definition based on $ A \cap B $, all $ A, B \subseteq S $ are "non-positively correlated" with respect to the disjoint intersection $ A \square B $.
References
| [a1] | R. Ahlswede, D.E. Daykin, "An inequality for the weights of two families, their unions and intersections" Z. Wahrscheinlichkeitsth. verw. Gebiete , 43 (1978) pp. 183–185 |
| [a2] | B. Bollobás, "Combinatorics" , Cambridge Univ. Press (1986) |
| [a3] | G.R. Brightwell, "Universal correlations in finite posets" Order , 2 (1985) pp. 129–144 |
| [a4] | G.R. Brightwell, "Some correlation inequalities in finite posets" Order , 2 (1986) pp. 387–402 |
| [a5] | D.E. Daykin, "A lattice is distributive if and only if 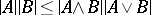 " Nanta Math. , 10 (1977) pp. 58–60 " Nanta Math. , 10 (1977) pp. 58–60 |
| [a6] | P.C. Fishburn, "A correlational inequality for linear extensions of a poset" Order , 1 (1984) pp. 127–137 |
| [a7] | P.C. Fishburn, "Correlation in partially ordered sets" Discrete Appl. Math. , 39 (1992) pp. 173–191 |
| [a8] | P.C. Fishburn, P.G. Doyle, L.A. Shepp, "The match set of a random permutation has the FKG property" Ann. of Probab. , 16 (1988) pp. 1194–1214 |
| [a9] | C.M. Fortuin, P.N. Kasteleyn, J. Ginibre, "Correlation inequalities for some partially ordered sets" Comm. Math. Phys. , 22 (1971) pp. 89–103 |
| [a10] | R.L. Graham, "Applications of the FKG inequality and its relatives" , Proc. 12th Internat. Symp. Math. Programming , Springer (1983) pp. 115–131 |
| [a11] | R.L Graham, A.C. Yao, F.F. Yao, "Some monotonicity properties of partial orders" SIAM J. Alg. Discrete Methods , 1 (1980) pp. 251–258 |
| [a12] | R. Holley, "Remarks on the FKG inequalities" Comm. Math. Phys. , 36 (1974) pp. 227–231 |
| [a13] | D.J. Kleitman, "Families of non-disjoint sets" J. Combin. Th. , 1 (1966) pp. 153–155 |
| [a14] | J. Marica, J. Schönheim, "Differences of sets and a problem of Graham" Canad. Math. Bull. , 12 (1969) pp. 635–637 |
| [a15] | D. Reimer, in preparation (to appear) |
| [a16] | P.D. Seymour, "On incomparable collections of sets" Mathematika , 20 (1973) pp. 208–209 |
| [a17] | L.A. Shepp, "The FKG property and some monotonicity properties of partial orders" SIAM J. Alg. Discrete Methods , 1 (1980) pp. 295–299 |
| [a18] | L.A. Shepp, "The XYZ conjecture and the FKG inequality" Ann. of Probab. , 10 (1982) pp. 824–827 |
| [a19] | R.F. Tate, "Correlation methods" W.H. Kruskal (ed.) J.M. Tanur (ed.) , Internat. Encycl. Stat. , 1 , Free Press (1978) pp. 615–628 |
| [a20] | J. van der Berg, U. Fiebig, "On a combinatorial conjecture concerning disjoint occurrences of events" Ann. of Probab. , 15 (1987) pp. 354–374 |
| [a21] | J. van der Berg, H. Kesten, "Inequalities with applications to percolation and reliability" J. Appl. Probab. , 22 (1985) pp. 556–569 |
| [a22] | P.M. Winkler, "Correlation among partial orders" SIAM J. Alg. Discrete Methods , 4 (1983) pp. 1–7 |
| [a23] | P M. Winkler, "Correlation and order" Contemp. Math. , 57 (1986) pp. 151–174 |
Correlation inequalities. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Correlation_inequalities&oldid=13617