Difference between revisions of "Complex space"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 18: | Line 18: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> B.V. Shabat, "Introduction of complex analysis" , '''1–2''' , Moscow (1976) (In Russian) {{MR|}} {{ZBL|0799.32001}} {{ZBL|0732.32001}} {{ZBL|0732.30001}} {{ZBL|0578.32001}} {{ZBL|0574.30001}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) (Translated from French) {{MR|0205211}} {{MR|0205210}} {{ZBL|0301.54002}} {{ZBL|0301.54001}} {{ZBL|0145.19302}} </TD></TR></table> |
| Line 26: | Line 26: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H. Grauert, R. Remmert, "Theory of Stein spaces" , Springer (1979) (Translated from German) {{MR|0580152}} {{ZBL|0433.32007}} </TD></TR></table> |
Revision as of 21:51, 30 March 2012
complex-analytic space
An analytic space over the field of complex numbers 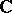 . The simplest and most widely used complex space is the complex number space
. The simplest and most widely used complex space is the complex number space 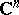 . Its points, or elements, are all possible
. Its points, or elements, are all possible  -tuples
-tuples 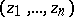 of complex numbers
of complex numbers 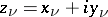 ,
, 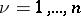 . It is a vector space over
. It is a vector space over 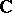 with the operations of addition
with the operations of addition
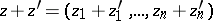 |
and multiplication by a scalar 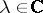 ,
,
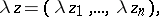 |
as well as a metric space with the Euclidean metric
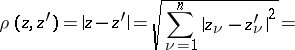 |
 |
In other words, the complex number space 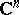 is obtained as the result of complexifying the real number space
is obtained as the result of complexifying the real number space 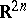 . The complex number space
. The complex number space 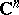 is also the topological product of
is also the topological product of  complex planes
complex planes  ,
, 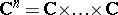 .
.
References
| [1] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian) Zbl 0799.32001 Zbl 0732.32001 Zbl 0732.30001 Zbl 0578.32001 Zbl 0574.30001 |
| [2] | N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) (Translated from French) MR0205211 MR0205210 Zbl 0301.54002 Zbl 0301.54001 Zbl 0145.19302 |
Comments
A more general notion of complex space is contained in [a1]. Roughly it is as follows. Let 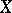 be a Hausdorff space equipped with asheaf
be a Hausdorff space equipped with asheaf 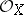 of local
of local 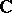 -algebras (a so-called
-algebras (a so-called 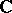 -algebraized space). Two such spaces
-algebraized space). Two such spaces  and
and  are called isomorphic if there is a homeomorphism
are called isomorphic if there is a homeomorphism 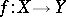 and a sheaf isomorphism
and a sheaf isomorphism 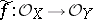 (cf. [a1]). Now, a
(cf. [a1]). Now, a 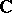 -algebraized space
-algebraized space 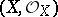 is called a complex manifold if it is locally isomorphic to a standard space
is called a complex manifold if it is locally isomorphic to a standard space 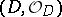 ,
, 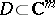 a domain,
a domain, 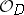 its sheaf of germs of holomorphic functions, i.e. if for every
its sheaf of germs of holomorphic functions, i.e. if for every 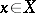 there is a neighbourhood
there is a neighbourhood 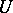 of
of  in
in 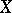 and a domain
and a domain 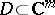 , for some
, for some  , so that the
, so that the 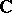 -algebraized spaces
-algebraized spaces 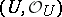 and
and 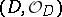 are isomorphic. Let
are isomorphic. Let 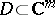 be a domain and
be a domain and  a coherent ideal. The support
a coherent ideal. The support 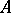 of the (coherent) quotient sheaf
of the (coherent) quotient sheaf 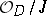 is a closed set in
is a closed set in 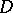 , and the sheaf
, and the sheaf 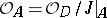 is a (coherent) sheaf of local
is a (coherent) sheaf of local 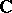 -algebras. The
-algebras. The 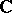 -algebraized space
-algebraized space 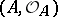 is called a (closed) complex subspace of
is called a (closed) complex subspace of 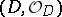 (it is naturally imbedded in
(it is naturally imbedded in 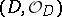 via the quotient sheaf mapping). A complex space
via the quotient sheaf mapping). A complex space 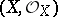 is a
is a 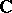 -algebraized space that is locally isomorphic to a complex subspace, i.e. every point
-algebraized space that is locally isomorphic to a complex subspace, i.e. every point 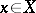 has a neighbourhood
has a neighbourhood 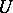 so that
so that 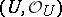 is isomorphic to a complex subspace of a domain in some
is isomorphic to a complex subspace of a domain in some 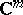 . (See also Sheaf theory; Coherent sheaf.) More on complex spaces, in particular their use in function theory of several variables and algebraic geometry, can be found in [a1]. See also Stein space; Analytic space.
. (See also Sheaf theory; Coherent sheaf.) More on complex spaces, in particular their use in function theory of several variables and algebraic geometry, can be found in [a1]. See also Stein space; Analytic space.
References
| [a1] | H. Grauert, R. Remmert, "Theory of Stein spaces" , Springer (1979) (Translated from German) MR0580152 Zbl 0433.32007 |
Complex space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complex_space&oldid=11574