Difference between revisions of "Cellular algebra"
m (link) |
m (AUTOMATIC EDIT (latexlist): Replaced 43 formulas out of 45 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 45 formulas, 43 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|partial}} | ||
''(in algebraic combinatorics)'' | ''(in algebraic combinatorics)'' | ||
Algebras introduced by B.Yu. Weisfeiler and A.A. Leman [[#References|[a9]]] and initially studied by representatives of the Soviet school of algebraic combinatorics. The first stage of this development was summarized in [[#References|[a8]]]. Important particular examples of cellular algebras are the coherent algebras (cf. also [[Coherent algebra|Coherent algebra]]). | Algebras introduced by B.Yu. Weisfeiler and A.A. Leman [[#References|[a9]]] and initially studied by representatives of the Soviet school of algebraic combinatorics. The first stage of this development was summarized in [[#References|[a8]]]. Important particular examples of cellular algebras are the coherent algebras (cf. also [[Coherent algebra|Coherent algebra]]). | ||
| − | A cellular algebra | + | A cellular algebra $W$ of order $n$ and rank $r$ is a matrix subalgebra of the full matrix algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130060/c1300604.png"/> of $( n \times n )$-matrices over $\mathbf{C}$ such that: |
| − | + | $W$ is closed with respect to the Hermitian adjoint; | |
| − | + | $J \in W$, where $J$ is the all-one matrix; | |
| − | + | $W$ is closed with respect to [[Schur–Hadamard multiplication]] (cf. also [[Coherent algebra]]). A coherent algebra is a cellular algebra that contains the unit matrix $I$. | |
| − | Like coherent algebras, a cellular algebra | + | Like coherent algebras, a cellular algebra $W$ has a unique standard basis of zero-one matrices $\{ A _ { 1 } , \dots , A _ { r } \}$, consisting of mutually orthogonal Schur–Hadamard idempotents. The notation $W = \langle A _ { 1 } , \dots , A _ { r } \rangle$ indicates that $W$ has the standard basis $\{ A _ { 1 } , \dots , A _ { r } \}$. |
| − | A cellular algebra | + | A cellular algebra $W$ is called a cell if the all unit matrix $J$ belongs to its centre (cf. also [[Centre of a ring|Centre of a ring]]). Cells containing the unit matrix $I$ are equivalent to Bose–Mesner algebras. If the entries of the matrices in $W$ are restricted to the ring $\bf Z$, then the corresponding ring of matrices is called a cellular ring. |
| − | The relational analogue of cellular algebras with the unit matrix | + | The relational analogue of cellular algebras with the unit matrix $I$ was introduced by D.G. Higman in [[#References|[a3]]] under the name coherent configuration. For a long time the theories of cellular algebras and coherent configurations were developed relatively independently. After the appearance of Higman's paper [[#References|[a4]]], where the terminology of coherent algebras was coined, most researchers switched to the terminology of coherent algebras. |
| − | As a rule, only cellular algebras containing | + | As a rule, only cellular algebras containing $I$ (that is, coherent algebras) were investigated. Situations where cellular algebras are required properly appear rarely, see for example [[#References|[a7]]], where a particular kind of such algebras are treated as pseudo-Schur rings. |
The initial motivation for the introduction of cellular algebras was the graph isomorphism problem (cf. also [[Graph isomorphism|Graph isomorphism]]). | The initial motivation for the introduction of cellular algebras was the graph isomorphism problem (cf. also [[Graph isomorphism|Graph isomorphism]]). | ||
| − | The intersection of cellular algebras is again a cellular algebra. For each set of matrices of the same order | + | The intersection of cellular algebras is again a cellular algebra. For each set of matrices of the same order $n$ it is possible to determine a minimal cellular algebra containing this set. In particular, if $\Gamma$ is an $n$-vertex graph and $A = A ( \Gamma )$ is its [[adjacency matrix]], then $\langle \langle A \rangle \rangle$ denotes the smallest cellular algebra containing $A$. It is called the cellular closure (or Weisfeiler–Leman closure) of $W$. |
| − | In [[#References|[a9]]] and [[#References|[a8]]], Weisfeiler and Leman described an algorithm of stabilization which has an input | + | In [[#References|[a9]]] and [[#References|[a8]]], Weisfeiler and Leman described an algorithm of stabilization which has an input $A$ and returns $\langle \langle A \rangle \rangle$ in polynomial time, depending on $n$. Isomorphic graphs have isomorphic cellular closures, and this fact has important applications, see [[#References|[a6]]]. In general, $\langle \langle A \rangle \rangle$ does not coincide with the centralizer algebra of the automorphism group of the graph $\Gamma$; however, they do coincide for many classes of graphs, for example for the algebraic forests introduced in [[#References|[a1]]]. |
| − | For each cellular algebra | + | For each cellular algebra $W = \langle A _ { 1 } , \dots , A _ { r } \rangle$ one can introduce its automorphism group |
| − | + | \begin{equation*} \operatorname { Aut } ( W ) = \cap _ { i = 1 } ^ { r } \operatorname { Aut } ( A _ { i } ). \end{equation*} | |
| − | Here, | + | Here, $\operatorname { Aut} ( A _ { i } )$ is the automorphism group of the graph $\Gamma_{i}$ with adjacency matrix $A _ { i } = A ( \Gamma _ { i } )$. For each [[Permutation group|permutation group]] $( G , \Omega )$, its centralizer algebra $\mathfrak { V } ( G , \Omega )$ is a cellular algebra with matrix $I$. Thus, the functors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130060/c13006044.png"/> and $\frak V$ introduce a [[Galois correspondence|Galois correspondence]] between cellular (coherent) algebras and permutation groups. Some properties and applications of this correspondence are considered in [[#References|[a2]]], [[#References|[a5]]]. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> S. Evdokimov, I. Ponomarenko, G. Tinhofer, "Forestal algebras and algebraic forests (on a new class of weakly compact graphs)" ''Discr. Math.'' , '''225''' (2000) pp. 149–172</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> I.A. Faradžev, M.H. Klin, M.E. Muzichuk, "Cellular rings and groups of automorphisms of graphs." I.A. Faradžev (ed.) et al. (ed.) , ''Investigations in Algebraic Theory of Combinatorial Objects'' , Kluwer Acad. Publ. (1994) pp. 1–152</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> D.G. Higman, "Coherent configurations I" ''Rend. Sem. Mat. Univ. Padova'' , '''44''' (1970) pp. 1–25</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> D.G. Higman, "Coherent algebras." ''Linear Alg. & Its Appl.'' , '''93''' (1987) pp. 209–239</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> A.A. Ivanov, I.A. Faradžev, M.H. Klin, "Galois correspondence between permutation groups and cellular rings (association schemes)" ''Graphs and Combinatorics'' , '''6''' (1990) pp. 303–332</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> M. Klin, C. Rücker, G. Rücker, G. Tinhofer, "Algebraic combinatorics in mathematical chemistry. Methods and algorithms. I. Permutation groups and coherent (cellular) algebras" ''MATCH'' , '''40''' (1999) pp. 7–138</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> M.E. Muzychuk, "The structure of rational Schur rings over cyclic groups" ''Europ. J. Combin.'' , '''14''' (1993) pp. 479–490</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> "On construction and identification of graphs" B. Weisfeiler (ed.) , ''Lecture Notes in Math.'' , '''558''' , Springer (1976)</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> B.Yu. Weisfeiler, A.A. Leman, "A reduction of a graph to a canonical form and an algebra arising during this reduction" ''Nauchno-Techn. Inform. Ser. 2'' , '''9''' (1968) pp. 12–16 (In Russian)</td></tr></table> |
Revision as of 17:02, 1 July 2020
(in algebraic combinatorics)
Algebras introduced by B.Yu. Weisfeiler and A.A. Leman [a9] and initially studied by representatives of the Soviet school of algebraic combinatorics. The first stage of this development was summarized in [a8]. Important particular examples of cellular algebras are the coherent algebras (cf. also Coherent algebra).
A cellular algebra $W$ of order $n$ and rank $r$ is a matrix subalgebra of the full matrix algebra  of $( n \times n )$-matrices over $\mathbf{C}$ such that:
of $( n \times n )$-matrices over $\mathbf{C}$ such that:
$W$ is closed with respect to the Hermitian adjoint;
$J \in W$, where $J$ is the all-one matrix;
$W$ is closed with respect to Schur–Hadamard multiplication (cf. also Coherent algebra). A coherent algebra is a cellular algebra that contains the unit matrix $I$.
Like coherent algebras, a cellular algebra $W$ has a unique standard basis of zero-one matrices $\{ A _ { 1 } , \dots , A _ { r } \}$, consisting of mutually orthogonal Schur–Hadamard idempotents. The notation $W = \langle A _ { 1 } , \dots , A _ { r } \rangle$ indicates that $W$ has the standard basis $\{ A _ { 1 } , \dots , A _ { r } \}$.
A cellular algebra $W$ is called a cell if the all unit matrix $J$ belongs to its centre (cf. also Centre of a ring). Cells containing the unit matrix $I$ are equivalent to Bose–Mesner algebras. If the entries of the matrices in $W$ are restricted to the ring $\bf Z$, then the corresponding ring of matrices is called a cellular ring.
The relational analogue of cellular algebras with the unit matrix $I$ was introduced by D.G. Higman in [a3] under the name coherent configuration. For a long time the theories of cellular algebras and coherent configurations were developed relatively independently. After the appearance of Higman's paper [a4], where the terminology of coherent algebras was coined, most researchers switched to the terminology of coherent algebras.
As a rule, only cellular algebras containing $I$ (that is, coherent algebras) were investigated. Situations where cellular algebras are required properly appear rarely, see for example [a7], where a particular kind of such algebras are treated as pseudo-Schur rings.
The initial motivation for the introduction of cellular algebras was the graph isomorphism problem (cf. also Graph isomorphism).
The intersection of cellular algebras is again a cellular algebra. For each set of matrices of the same order $n$ it is possible to determine a minimal cellular algebra containing this set. In particular, if $\Gamma$ is an $n$-vertex graph and $A = A ( \Gamma )$ is its adjacency matrix, then $\langle \langle A \rangle \rangle$ denotes the smallest cellular algebra containing $A$. It is called the cellular closure (or Weisfeiler–Leman closure) of $W$.
In [a9] and [a8], Weisfeiler and Leman described an algorithm of stabilization which has an input $A$ and returns $\langle \langle A \rangle \rangle$ in polynomial time, depending on $n$. Isomorphic graphs have isomorphic cellular closures, and this fact has important applications, see [a6]. In general, $\langle \langle A \rangle \rangle$ does not coincide with the centralizer algebra of the automorphism group of the graph $\Gamma$; however, they do coincide for many classes of graphs, for example for the algebraic forests introduced in [a1].
For each cellular algebra $W = \langle A _ { 1 } , \dots , A _ { r } \rangle$ one can introduce its automorphism group
\begin{equation*} \operatorname { Aut } ( W ) = \cap _ { i = 1 } ^ { r } \operatorname { Aut } ( A _ { i } ). \end{equation*}
Here, $\operatorname { Aut} ( A _ { i } )$ is the automorphism group of the graph $\Gamma_{i}$ with adjacency matrix $A _ { i } = A ( \Gamma _ { i } )$. For each permutation group $( G , \Omega )$, its centralizer algebra $\mathfrak { V } ( G , \Omega )$ is a cellular algebra with matrix $I$. Thus, the functors 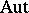 and $\frak V$ introduce a Galois correspondence between cellular (coherent) algebras and permutation groups. Some properties and applications of this correspondence are considered in [a2], [a5].
and $\frak V$ introduce a Galois correspondence between cellular (coherent) algebras and permutation groups. Some properties and applications of this correspondence are considered in [a2], [a5].
References
| [a1] | S. Evdokimov, I. Ponomarenko, G. Tinhofer, "Forestal algebras and algebraic forests (on a new class of weakly compact graphs)" Discr. Math. , 225 (2000) pp. 149–172 |
| [a2] | I.A. Faradžev, M.H. Klin, M.E. Muzichuk, "Cellular rings and groups of automorphisms of graphs." I.A. Faradžev (ed.) et al. (ed.) , Investigations in Algebraic Theory of Combinatorial Objects , Kluwer Acad. Publ. (1994) pp. 1–152 |
| [a3] | D.G. Higman, "Coherent configurations I" Rend. Sem. Mat. Univ. Padova , 44 (1970) pp. 1–25 |
| [a4] | D.G. Higman, "Coherent algebras." Linear Alg. & Its Appl. , 93 (1987) pp. 209–239 |
| [a5] | A.A. Ivanov, I.A. Faradžev, M.H. Klin, "Galois correspondence between permutation groups and cellular rings (association schemes)" Graphs and Combinatorics , 6 (1990) pp. 303–332 |
| [a6] | M. Klin, C. Rücker, G. Rücker, G. Tinhofer, "Algebraic combinatorics in mathematical chemistry. Methods and algorithms. I. Permutation groups and coherent (cellular) algebras" MATCH , 40 (1999) pp. 7–138 |
| [a7] | M.E. Muzychuk, "The structure of rational Schur rings over cyclic groups" Europ. J. Combin. , 14 (1993) pp. 479–490 |
| [a8] | "On construction and identification of graphs" B. Weisfeiler (ed.) , Lecture Notes in Math. , 558 , Springer (1976) |
| [a9] | B.Yu. Weisfeiler, A.A. Leman, "A reduction of a graph to a canonical form and an algebra arising during this reduction" Nauchno-Techn. Inform. Ser. 2 , 9 (1968) pp. 12–16 (In Russian) |
Cellular algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cellular_algebra&oldid=50442