Difference between revisions of "Borel transform"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 30: | Line 30: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E. Borel, "Leçons sur les series divergentes" , Gauthier-Villars (1928) {{MR|}} {{ZBL|54.0223.01}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M.M. Dzhrbashyan, "Integral transforms and representation of functions in the complex domain" , Moscow (1966) (In Russian)</TD></TR></table> |
| Line 38: | Line 38: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.P. Boas, "Entire functions" , Acad. Press (1954) {{MR|0068627}} {{ZBL|0058.30201}} </TD></TR></table> |
Revision as of 16:55, 15 April 2012
An integral transform of the type
 |
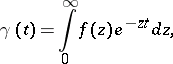where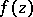 
is an entire function of exponential type. The Borel transform is a special case of the Laplace transform. The function 
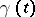is called the Borel transform of 
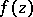. If
 |
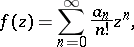then
 |
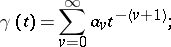the series converges for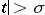 
, where 
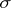is the type of 
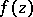. Let 
be the smallest closed convex set containing all the singularities of the function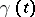 
; let
 |
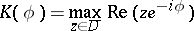be the supporting function of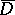 
; and let 
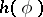be the growth indicator function of 
; then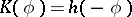 
. If in a Borel transform the integration takes place over a ray 
, the corresponding integral will converge in the half-plane 
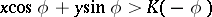. Let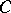 
be a closed contour surrounding 
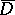; then
 |
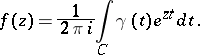If additional conditions are imposed, other representations may be deduced from this formula. Thus, consider the class of entire functions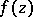 
of exponential type 
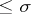for which
 |
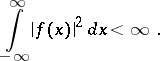This class is identical with the class of functions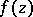 
that can be represented as
 |
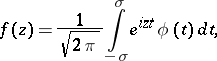where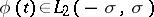 
.
References
| [1] | E. Borel, "Leçons sur les series divergentes" , Gauthier-Villars (1928) Zbl 54.0223.01 |
| [2] | M.M. Dzhrbashyan, "Integral transforms and representation of functions in the complex domain" , Moscow (1966) (In Russian) |
Comments
The statement at the end of the article above is called the Paley–Wiener theorem.
References
| [a1] | R.P. Boas, "Entire functions" , Acad. Press (1954) MR0068627 Zbl 0058.30201 |
Borel transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Borel_transform&oldid=18485