Difference between revisions of "Bianchi group"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | b1105001.png | ||
| + | $#A+1 = 37 n = 1 | ||
| + | $#C+1 = 37 : ~/encyclopedia/old_files/data/B110/B.1100500 Bianchi group | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | For a positive square-free integer $ d > 0 $, | |
| + | the Bianchi group $ \Gamma _ {d} $ | ||
| + | is the group $ PSL _ {2} ( {\mathcal O} _ {d} ) $, | ||
| + | where $ {\mathcal O} _ {d} $ | ||
| + | is the ring of integers in the imaginary quadratic number field $ \mathbf Q ( \sqrt {- d } ) $. | ||
| + | This class of groups is of interest in may different areas. In algebra they arise as the simplest numerically defined discrete groups. In number theory they have been used to study the zeta-functions of binary Hermitian forms over the rings $ {\mathcal O} _ {d} $. | ||
| + | Finally, they are of interest in the theory of Fuchsian groups (cf. [[Fuchsian group|Fuchsian group]]) and the related theory of Riemann surfaces (cf. [[Riemann surface|Riemann surface]]). The Bianchi groups can be considered as the natural algebraic generalization of the classical [[Modular group|modular group]] $ PSL _ {2} ( \mathbf Z ) $. | ||
| + | A good general reference for the Bianchi groups and their relation to the modular group is [[#References|[a2]]]. For $ d = 1,2,3,7,11 $ | ||
| + | the rings $ {\mathcal O} _ {d} $ | ||
| + | have Euclidean algorithms (cf. [[Euclidean algorithm|Euclidean algorithm]]) and the corresponding groups $ \Gamma _ {d} $ | ||
| + | are the Euclidean Bianchi groups. As is to be expected, these are much closer in properties to the modular group than in the non-Euclidean cases. Of particular interest is the group $ \Gamma _ {1} $, | ||
| + | which is called the Picard group. | ||
| − | + | A general method to determine finite presentations for each $ \Gamma _ {d} $ | |
| + | was developed by R. Swan [[#References|[a5]]] based on geometrical work of L. Bianchi, while a separate purely algebraic method was given by P.M. Cohn [[#References|[a1]]]. A computer implementation of Swan's method was derived by R. Riley [[#References|[a3]]]. | ||
| − | + | Algebraic interest centred on two questions raised in the work of J.-P. Serre. First, Serre showed (see [[#References|[a4]]]) that for $ d \neq 3 $ | |
| + | these groups do not satisfy property FA. It was thus conjectured that they were all non-trivial free products with amalgamation. This was proved by B. Fine in the Euclidean cases and by Fine and C. Frohmann in general using topological methods. In summary: | ||
| − | + | 1) For each $ d \neq 3 $, | |
| + | the Bianchi group $ \Gamma _ {d} $ | ||
| + | decomposes as a non-trivial free product with amalgamation. If $ d \neq 1,2,7,11 $, | ||
| + | one has $ \Gamma _ {d} = PE _ {2} ( {\mathcal O} _ {d} ) \star _ {H _ {d} } G _ {d} $, | ||
| + | where $ PE _ {2} ( {\mathcal O} _ {d} ) $ | ||
| + | is the group of projective elementary matrices over $ {\mathcal O} _ {d} $, | ||
| + | $ G _ {d} $ | ||
| + | is a group depending on $ d $, | ||
| + | and the amalgamated subgroup $ H _ {d} $ | ||
| + | is an amalgam of two copies of the modular group. | ||
| + | |||
| + | The second of Serre's questions involved the congruence subgroup property. If $ R $ | ||
| + | is a commutative ring and $ I $ | ||
| + | is an ideal in $ R $, | ||
| + | the mapping $ R \rightarrow R/I $ | ||
| + | induces a mapping $ SL _ {n} ( R ) \rightarrow SL _ {n} ( R/I ) $. | ||
| + | The kernel of this mapping is called the principal congruence subgroup modulo $ I $. | ||
| + | A [[Congruence subgroup|congruence subgroup]] is a subgroup of finite index containing a principal congruence subgroup. H. Bass, J. Milnor and Serre proved that in $ SL _ {n} ( R ) $ | ||
| + | for $ n \geq 3 $, | ||
| + | every subgroup of finite index is a congruence subgroup. This is false in the modular group and Serre proved that: | ||
| + | |||
| + | 2) For each $ d $ | ||
| + | the Bianchi group $ \Gamma _ {d} $ | ||
| + | contains non-congruence subgroups of finite index. | ||
Another proof of this using the theory of pro-finite groups was given by A.E. Lubotzky. | Another proof of this using the theory of pro-finite groups was given by A.E. Lubotzky. | ||
| − | Other questions on the Bianchi groups involved their Fuchsian subgroups. Fine determined the structure of such Fuchsian imbeddings while C. Maclachlan and A. Reid dealt with arithmetic Fuchsian groups (see [[#References|[a2]]]). Work has also been done on the homology of the group | + | Other questions on the Bianchi groups involved their Fuchsian subgroups. Fine determined the structure of such Fuchsian imbeddings while C. Maclachlan and A. Reid dealt with arithmetic Fuchsian groups (see [[#References|[a2]]]). Work has also been done on the homology of the group $ \Gamma _ {d} $ |
| + | and on the structure of the $ 3 $- | ||
| + | manifolds $ {\mathcal H} ^ {3} / \Gamma _ {d} $, | ||
| + | where $ {\mathcal H} ^ {3} $ | ||
| + | is hyperbolic $ 3 $- | ||
| + | dimensional space (see [[#References|[a2]]] for complete references). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.M. Cohn, "A presentation for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110500/b11050038.png" /> for Euclidean quadratic imaginary number fields" ''Mathematika'' , '''15''' (1968) pp. 156–163</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> B. Fine, "Algebraic theory of the Bianchi groups" , M. Dekker (1989)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> R. Riley, "Applications of a computer implementation of Poincaré's theorem on fundamental polyhedra" ''Math. of Comp.'' , '''40''' (1983) pp. 1607–632</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J.P. Serre, "Trees" , Springer (1980)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> R.G. Swan, "Generators and relations for certain special linear groups" ''Adv. in Math.'' , '''6''' (1971) pp. 1–77</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.M. Cohn, "A presentation for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110500/b11050038.png" /> for Euclidean quadratic imaginary number fields" ''Mathematika'' , '''15''' (1968) pp. 156–163</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> B. Fine, "Algebraic theory of the Bianchi groups" , M. Dekker (1989)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> R. Riley, "Applications of a computer implementation of Poincaré's theorem on fundamental polyhedra" ''Math. of Comp.'' , '''40''' (1983) pp. 1607–632</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J.P. Serre, "Trees" , Springer (1980)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> R.G. Swan, "Generators and relations for certain special linear groups" ''Adv. in Math.'' , '''6''' (1971) pp. 1–77</TD></TR></table> | ||
Revision as of 10:58, 29 May 2020
For a positive square-free integer $ d > 0 $,
the Bianchi group $ \Gamma _ {d} $
is the group $ PSL _ {2} ( {\mathcal O} _ {d} ) $,
where $ {\mathcal O} _ {d} $
is the ring of integers in the imaginary quadratic number field $ \mathbf Q ( \sqrt {- d } ) $.
This class of groups is of interest in may different areas. In algebra they arise as the simplest numerically defined discrete groups. In number theory they have been used to study the zeta-functions of binary Hermitian forms over the rings $ {\mathcal O} _ {d} $.
Finally, they are of interest in the theory of Fuchsian groups (cf. Fuchsian group) and the related theory of Riemann surfaces (cf. Riemann surface). The Bianchi groups can be considered as the natural algebraic generalization of the classical modular group $ PSL _ {2} ( \mathbf Z ) $.
A good general reference for the Bianchi groups and their relation to the modular group is [a2]. For $ d = 1,2,3,7,11 $
the rings $ {\mathcal O} _ {d} $
have Euclidean algorithms (cf. Euclidean algorithm) and the corresponding groups $ \Gamma _ {d} $
are the Euclidean Bianchi groups. As is to be expected, these are much closer in properties to the modular group than in the non-Euclidean cases. Of particular interest is the group $ \Gamma _ {1} $,
which is called the Picard group.
A general method to determine finite presentations for each $ \Gamma _ {d} $ was developed by R. Swan [a5] based on geometrical work of L. Bianchi, while a separate purely algebraic method was given by P.M. Cohn [a1]. A computer implementation of Swan's method was derived by R. Riley [a3].
Algebraic interest centred on two questions raised in the work of J.-P. Serre. First, Serre showed (see [a4]) that for $ d \neq 3 $ these groups do not satisfy property FA. It was thus conjectured that they were all non-trivial free products with amalgamation. This was proved by B. Fine in the Euclidean cases and by Fine and C. Frohmann in general using topological methods. In summary:
1) For each $ d \neq 3 $, the Bianchi group $ \Gamma _ {d} $ decomposes as a non-trivial free product with amalgamation. If $ d \neq 1,2,7,11 $, one has $ \Gamma _ {d} = PE _ {2} ( {\mathcal O} _ {d} ) \star _ {H _ {d} } G _ {d} $, where $ PE _ {2} ( {\mathcal O} _ {d} ) $ is the group of projective elementary matrices over $ {\mathcal O} _ {d} $, $ G _ {d} $ is a group depending on $ d $, and the amalgamated subgroup $ H _ {d} $ is an amalgam of two copies of the modular group.
The second of Serre's questions involved the congruence subgroup property. If $ R $ is a commutative ring and $ I $ is an ideal in $ R $, the mapping $ R \rightarrow R/I $ induces a mapping $ SL _ {n} ( R ) \rightarrow SL _ {n} ( R/I ) $. The kernel of this mapping is called the principal congruence subgroup modulo $ I $. A congruence subgroup is a subgroup of finite index containing a principal congruence subgroup. H. Bass, J. Milnor and Serre proved that in $ SL _ {n} ( R ) $ for $ n \geq 3 $, every subgroup of finite index is a congruence subgroup. This is false in the modular group and Serre proved that:
2) For each $ d $ the Bianchi group $ \Gamma _ {d} $ contains non-congruence subgroups of finite index.
Another proof of this using the theory of pro-finite groups was given by A.E. Lubotzky.
Other questions on the Bianchi groups involved their Fuchsian subgroups. Fine determined the structure of such Fuchsian imbeddings while C. Maclachlan and A. Reid dealt with arithmetic Fuchsian groups (see [a2]). Work has also been done on the homology of the group $ \Gamma _ {d} $ and on the structure of the $ 3 $- manifolds $ {\mathcal H} ^ {3} / \Gamma _ {d} $, where $ {\mathcal H} ^ {3} $ is hyperbolic $ 3 $- dimensional space (see [a2] for complete references).
References
| [a1] | P.M. Cohn, "A presentation for 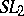 for Euclidean quadratic imaginary number fields" Mathematika , 15 (1968) pp. 156–163 for Euclidean quadratic imaginary number fields" Mathematika , 15 (1968) pp. 156–163 |
| [a2] | B. Fine, "Algebraic theory of the Bianchi groups" , M. Dekker (1989) |
| [a3] | R. Riley, "Applications of a computer implementation of Poincaré's theorem on fundamental polyhedra" Math. of Comp. , 40 (1983) pp. 1607–632 |
| [a4] | J.P. Serre, "Trees" , Springer (1980) |
| [a5] | R.G. Swan, "Generators and relations for certain special linear groups" Adv. in Math. , 6 (1971) pp. 1–77 |
Bianchi group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bianchi_group&oldid=15524