Baric algebra
weighted algebra
In 1939, in connection with the formalism of genetics, I.M.H. Etherington introduced the notion of baric algebra (cf. [a1]; more commonly it is also called a weighted algebra). If 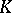 is a (commutative) field and
is a (commutative) field and 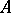 a
a 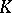 -algebra, not necessarily commutative or associative, one says that
-algebra, not necessarily commutative or associative, one says that 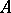 is a weighted algebra if there exists an algebra morphism
is a weighted algebra if there exists an algebra morphism 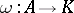 which is non-trivial. This means that one can write
which is non-trivial. This means that one can write 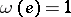 , where
, where  is a convenient element of
is a convenient element of 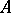 . The morphism
. The morphism 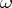 is called the weight function of
is called the weight function of 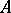 and one can regard a weighted algebra as a pair
and one can regard a weighted algebra as a pair 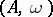 where
where 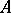 is an algebra and
is an algebra and 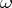 the weight function. A morphism
the weight function. A morphism 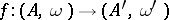 of weighted algebras is a morphism of algebras
of weighted algebras is a morphism of algebras 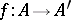 such that
such that 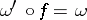 . This gives a category, the category of weighted algebras. All constructions on weighted algebras are made in this category. For a finite-dimensional
. This gives a category, the category of weighted algebras. All constructions on weighted algebras are made in this category. For a finite-dimensional 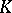 -algebra
-algebra 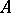 , the following conditions are equivalent:
, the following conditions are equivalent:
i) 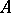 is a weighted algebra;
is a weighted algebra;
ii) there exists a finite basis  of
of 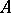 over
over 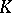 such that if
such that if 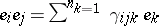 (
(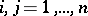 ) is the multiplication table of
) is the multiplication table of 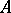 in this basis (the scalars
in this basis (the scalars 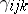 (
(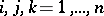 ) are the structure constants of
) are the structure constants of 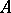 ), then
), then 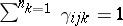 (
(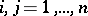 );
);
iii) there exists a two-sided ideal 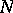 of
of 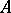 , of codimension one, such that
, of codimension one, such that 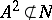 .
.
It is easy to see that a Lie algebra is not weighted; however, over any weighted algebra 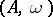 one can define a Lie algebra structure via the multiplication (bracket)
one can define a Lie algebra structure via the multiplication (bracket) 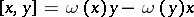 for all
for all 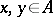 . A Jordan algebra may or may not be weighted; however, over any weighted algebra
. A Jordan algebra may or may not be weighted; however, over any weighted algebra 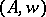 one can define a Jordan algebra structure via the multiplication
one can define a Jordan algebra structure via the multiplication 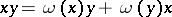 for all
for all 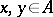 . A weighted algebra is not necessarily associative (cf. Associative rings and algebras); however, over any weighted algebra
. A weighted algebra is not necessarily associative (cf. Associative rings and algebras); however, over any weighted algebra 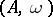 with a unit
with a unit  one can define an associative algebra structure via the multiplication
one can define an associative algebra structure via the multiplication 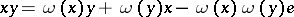 for all
for all 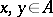 . A Clifford algebra is not weighted; in particular, the algebra of complex numbers and the algebra of quaternions are not weighted. All Bernstein algebras are weighted (cf. Bernstein algebra).
. A Clifford algebra is not weighted; in particular, the algebra of complex numbers and the algebra of quaternions are not weighted. All Bernstein algebras are weighted (cf. Bernstein algebra).
References
| [a1] | I.M.H. Etherington, "Genetic algebras" Proc. Roy. Soc. Edinburgh , 59 (1939) pp. 242–258 |
| [a2] | D. McHale, G.A. Ringwood, "Haldane linearisation of baric algebras" J. London Math. Soc. (2) , 28 (1983) pp. 17–26 |
| [a3] | A. Micali, Ph. Revoy, "Sur les algèbres gamétiques" Proc. Edinburgh Math. Soc , 29 (1986) pp. 187–197 |
| [a4] | M.K. Singh, D.K. Singh, "On baric algebras" The Math. Education (2) , 20 (1986) pp. 54–55 |
Baric algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Baric_algebra&oldid=16628