Approximate limit
A limit of a function 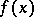 as
as  over a set
over a set 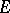 for which
for which 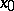 is a density point. In the simplest case
is a density point. In the simplest case 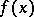 is a real-valued function of the points of an
is a real-valued function of the points of an  -dimensional Euclidean space; in the more general case it is a vector function. The approximate limit is denoted by
-dimensional Euclidean space; in the more general case it is a vector function. The approximate limit is denoted by
 |
In general, the existence of an ordinary limit does not follow from the existence of an approximate limit. An approximate limit displays the elementary properties of limits — uniqueness, and theorems on the limit of a sum, difference, product and quotient of two functions.
Let 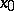 be a density point of the domain of definition of a real-valued function
be a density point of the domain of definition of a real-valued function 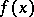 . If the ordinary limit
. If the ordinary limit 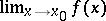 exists, the approximate limit also exists and is equal to it. The approximate upper limit of a function
exists, the approximate limit also exists and is equal to it. The approximate upper limit of a function 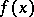 at a point
at a point 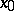 is the lower bound of the set of numbers
is the lower bound of the set of numbers 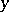 (including
(including 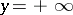 ) for which
) for which 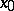 is a point of dispersion of the set
is a point of dispersion of the set 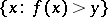 . Similarly, the approximate lower limit of a function
. Similarly, the approximate lower limit of a function  at a point
at a point 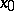 is the upper bound of the set of points
is the upper bound of the set of points 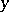 (including
(including 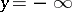 ) for which
) for which 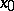 is a point of dispersion of the set
is a point of dispersion of the set 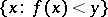 . These approximate limits are denoted, respectively, by
. These approximate limits are denoted, respectively, by
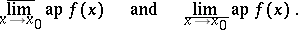 |
An approximate limit exists if and only if the approximate upper and lower limits are equal; their common value is equal to the approximate limit.
If  is real, one-sided (right and left) approximate upper and lower limits are also used (
is real, one-sided (right and left) approximate upper and lower limits are also used (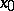 must then be, respectively, a right-hand or left-hand density point in the domain of definition of the function). For the approximate right upper limit the following notation is used:
must then be, respectively, a right-hand or left-hand density point in the domain of definition of the function). For the approximate right upper limit the following notation is used:
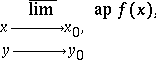 |
with corresponding notations for the other cases. If the approximate right upper and lower limits coincide, one obtains the right approximate limit; if the approximate left upper and lower limits coincide, one obtains the left approximate limit.
Approximate limits were first utilized by A. Denjoy and A.Ya. Khinchin in the study of the differential connections between an indefinite integral (in the sense of Lebesgue and in the sense of Denjoy–Khinchin) and the integrand (cf. Approximate continuity; Approximate derivative).
References
| [1] | S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) |
Comments
A point of dispersion is defined as follows: Let 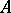 be a set in
be a set in 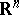 . Let
. Let 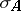 be the completely-additive set function defined for measurable
be the completely-additive set function defined for measurable 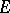 by
by 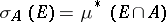 , the outer measure of
, the outer measure of 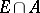 . Let
. Let  be any point in
be any point in 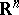 . The upper strong derivative and lower strong derivative
. The upper strong derivative and lower strong derivative 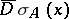 and
and 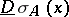 are called, respectively, the upper outer density and lower outer density of
are called, respectively, the upper outer density and lower outer density of 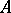 at
at  . The point
. The point  is a point of density for a set
is a point of density for a set 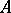 if the outer density of
if the outer density of 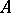 at
at  is 1 and it is a point of dispersion if the outer density of
is 1 and it is a point of dispersion if the outer density of 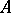 at
at  is zero. If
is zero. If 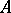 is measurable, almost-all points of
is measurable, almost-all points of 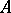 are points of density and almost-all points of its complement are points of dispersion. The latter condition is also sufficient for
are points of density and almost-all points of its complement are points of dispersion. The latter condition is also sufficient for 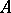 to be measurable.
to be measurable.
References
| [a1] | A.M. Bruckner, "Differentiation of real functions" , Springer (1978) |
| [a2] | M.E. Munroe, "Introduction to measure and integration" , Addison-Wesley (1953) pp. 111 |
| [a3] | B.S. Thomson, "Real functions" , Springer (1985) |
Approximate limit. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Approximate_limit&oldid=13657