Absolutely convergent improper integral
An improper integral such that the integral of the absolute value of the integrand converges. If an improper integral is absolutely convergent, it is also convergent. To take a concrete example, let an improper integral be given by
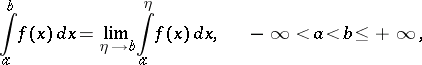 | (*) |
where the function 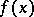 is Riemann- (or Lebesgue-) integrable on all intervals
is Riemann- (or Lebesgue-) integrable on all intervals 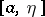 ,
, 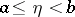 .
.
A necessary and sufficient condition for the absolute convergence of the integral (*) (Cauchy's criterion for the absolute convergence of an improper integral) is that for any 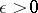 there must exist an
there must exist an 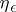 ,
, 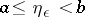 , such that for any
, such that for any 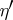 and
and 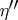 ,
, 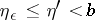 ,
, 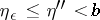 , the inequality
, the inequality
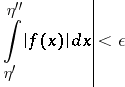 |
is true.
If the improper integral is absolutely convergent, then it is equal to the Lebesgue integral of the integrand. There exist improper integrals which are convergent but not absolutely convergent, for example
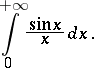 |
In order to find out whether or not a given integral is absolutely convergent it is expedient to use the tests for convergence of improper integrals of non-negative functions; for example, the absolute convergence of
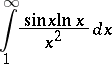 |
is established with the aid of the comparison criterion of convergence.
For most of the available definitions of multiple improper integrals there is a different relation between convergence and absolute convergence. Let a function 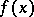 be defined on an open set
be defined on an open set  in the
in the  -dimensional Euclidean space. If, for any sequence of cube-filled domains
-dimensional Euclidean space. If, for any sequence of cube-filled domains 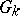 ,
,  which monotonically exhaust
which monotonically exhaust 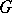 (i.e.
(i.e. 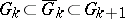 , and
, and
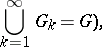 |
the limit of the Riemann integrals
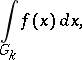 |
as 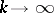 , exists and if this limit is independent of the choice of the above sequence of domains, then it is usually called the improper integral
, exists and if this limit is independent of the choice of the above sequence of domains, then it is usually called the improper integral
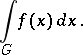 |
The integral thus defined is convergent if and only if it is absolutely convergent. There are also other definitions of multiple improper integrals. For example, for a function 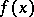 which is defined on the whole space
which is defined on the whole space  and which is Riemann-integrable on any
and which is Riemann-integrable on any  -dimensional sphere
-dimensional sphere  of radius
of radius  with centre at the origin, one can define the improper integral over
with centre at the origin, one can define the improper integral over 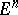 by the equation:
by the equation:
 |
The absolute convergence of the integral then implies its convergence, but the converse proposition is not true.
References
| [1] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1–2 , MIR (1982) (Translated from Russian) |
| [2] | L.D. Kudryavtsev, "Mathematical analysis" , 1 , Moscow (1973) (In Russian) |
| [3] | S.M. Nikol'skii, "A course of mathematical analysis" , 1 , MIR (1977) (Translated from Russian) |
Comments
References
| [a1] | T.M. Apostol, "Mathematical analysis" , Addison-Wesley (1969) |
Absolutely convergent improper integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Absolutely_convergent_improper_integral&oldid=12585