Difference between revisions of "Absolutely-unbiased sequence"
(Importing text file) |
(→References: Feller: internal link) |
||
| Line 11: | Line 11: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Feller, [[Feller, "An introduction to probability theory and its applications"|"An introduction to probability theory and its applications"]], '''2''', Wiley (1966) pp. 210</TD></TR></table> |
Revision as of 09:12, 4 May 2012
A sequence of random variables 
for which the conditions
 |
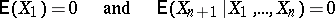are fulfilled, for 
. The partial sums 
of an absolutely-unbiased sequence form a martingale. These two types of sequences are interconnected as follows: The sequence 
forms a martingale if and only if it is of the form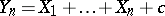 
(
and 
is a constant), where 
is an absolutely-unbiased sequence. Thus, all martingales are related to partial sums of certain absolutely-unbiased sequences. Simple examples of absolutely-unbiased sequences are sequences of independent random variables with mathematical expectation zero. Besides the term "unbiased" the term "fair" — with the related concept of a "fair play" , is also employed.
Comments
In [a1] the term "absolutely fair sequenceabsolutely fair" is used instead of absolutely-unbiased.
References
| [a1] | W. Feller, "An introduction to probability theory and its applications", 2, Wiley (1966) pp. 210 |
Absolutely-unbiased sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Absolutely-unbiased_sequence&oldid=13957