Chaplygin theorem

on differential inequalities

If in the differential inequality

(*)

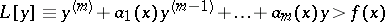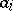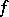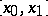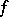all the and are summable on , then there exists an , independent of , such that 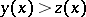, , 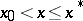where

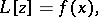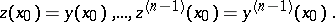Here

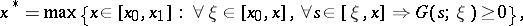where 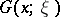is the corresponding Cauchy function, i.e. the solution of the equation 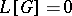, , 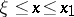that satisfies the initial conditions

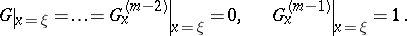Thus, for 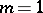, and also for the inequality 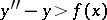, one obtains 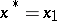, while for the inequality 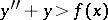one obtains

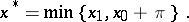Analogous statements hold: for weak inequalities; for the comparison of 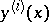with 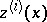, 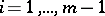; for initial conditions of the form

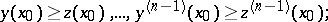and for solutions of the inequality (*) with .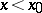

The theorem was obtained by S.A. Chaplygin in 1919.

See also the references in Differential inequality.

References

[1]	Ya.D. Mamedov, S. Ashirov, S. Atdaev, "Theorems on inequalities" , Ashkhabad (1980) (In Russian)

Comments

On page 123 of [a1] Chaplygin's theorem is formulated as a problem.

References

[a1]	I.G. Petrovskii, "Ordinary differential equations" , Prentice-Hall (1966) (Translated from Russian)