Uniformization
of a set 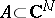 (or
(or 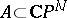 )
)
A triple 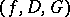 , where
, where 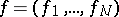 is a system of meromorphic functions in a domain
is a system of meromorphic functions in a domain 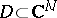 (respectively,
(respectively, 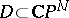 ), defining a holomorphic covering
), defining a holomorphic covering 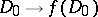 , where
, where 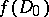 is dense in
is dense in 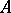 , and
, and  is a properly-discontinuous group of biholomorphic automorphisms of
is a properly-discontinuous group of biholomorphic automorphisms of 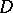 whose restriction to
whose restriction to 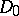 is the group of covering homeomorphisms of this covering, i.e.
is the group of covering homeomorphisms of this covering, i.e. 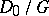 is biholomorphically equivalent to
is biholomorphically equivalent to 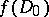 .
.
One may thus speak of uniformization by multi-valued analytic functions 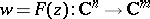 , by which one understands uniformization of the set
, by which one understands uniformization of the set 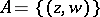 ; this corresponds to the parametrization of
; this corresponds to the parametrization of 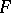 by means of single-valued meromorphic functions.
by means of single-valued meromorphic functions.
For example, the complex curve  in
in 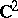 is uniformized by the triple
is uniformized by the triple 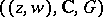 , where
, where 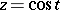 ,
, 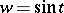 ,
, 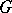 is the group of translations
is the group of translations 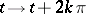 ,
, 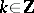 , or the triple
, or the triple 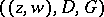 , where
, where
 |
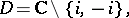 |
and 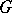 is the trivial group. A less trivial example is the cubic curve
is the trivial group. A less trivial example is the cubic curve  , which admits no rational parametrization, but which may be uniformized by means of elliptic functions (cf. Elliptic function), namely by a triple
, which admits no rational parametrization, but which may be uniformized by means of elliptic functions (cf. Elliptic function), namely by a triple 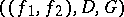 , where
, where 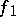 and
and 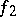 are rational functions in the Weierstrass
are rational functions in the Weierstrass 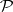 -function and its derivative, with corresponding periods
-function and its derivative, with corresponding periods 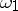 ,
,  , and
, and 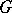 is the group generated by the translations
is the group generated by the translations 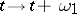 ,
, 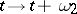 .
.
The problem of uniformizing an arbitrary algebraic curve defined by a general algebraic equation
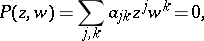 | (*) |
where 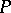 is an irreducible algebraic polynomial over
is an irreducible algebraic polynomial over 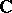 , arose already in the first half of the 19th century, particularly in connection with the integration of algebraic functions. H. Poincaré raised the question of the uniformization of the set of solutions of an arbitrary analytic equation of the form (*), when
, arose already in the first half of the 19th century, particularly in connection with the integration of algebraic functions. H. Poincaré raised the question of the uniformization of the set of solutions of an arbitrary analytic equation of the form (*), when  is a convergent power series in two variables, considered with all possible analytic continuations of it. The uniformization of algebraic and arbitrary analytic varieties constituted Hilbert's twenty-second problem. A complete solution of the uniformization problem has so far (1992) not been obtained, with the exception of the one-dimensional case.
is a convergent power series in two variables, considered with all possible analytic continuations of it. The uniformization of algebraic and arbitrary analytic varieties constituted Hilbert's twenty-second problem. A complete solution of the uniformization problem has so far (1992) not been obtained, with the exception of the one-dimensional case.
One introduces on the set of pairs 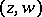 in
in 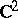 satisfying (*) a complex structure by means of elements of the corresponding algebraic function
satisfying (*) a complex structure by means of elements of the corresponding algebraic function 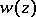 (or
(or 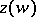 ), and so obtains a compact Riemann surface; the coordinates of points of the curve (*) are meromorphic functions on this surface. Furthermore, all compact Riemann surfaces, up to conformal equivalence, are obtained in this way. Therefore the problem of uniformization of algebraic curves is contained in the problem of uniformization of Riemann surfaces.
), and so obtains a compact Riemann surface; the coordinates of points of the curve (*) are meromorphic functions on this surface. Furthermore, all compact Riemann surfaces, up to conformal equivalence, are obtained in this way. Therefore the problem of uniformization of algebraic curves is contained in the problem of uniformization of Riemann surfaces.
A uniformization of an arbitrary Riemann surface 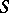 is a triple
is a triple 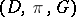 where
where 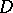 is a domain on the Riemann sphere
is a domain on the Riemann sphere  and
and 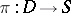 is a regular holomorphic covering with covering group
is a regular holomorphic covering with covering group 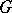 of conformal automorphisms of
of conformal automorphisms of 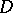 . The general problem consists in finding and describing all such triples for a given Riemann surface.
. The general problem consists in finding and describing all such triples for a given Riemann surface.
The possibility of uniformizing an arbitrary Riemann surface 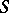 , giving in principle the solution of the problem, was achieved in the classical papers of P. Koebe, Poincaré and F. Klein; a complete solution was obtained, giving a description of all possible uniformizations of the surface
, giving in principle the solution of the problem, was achieved in the classical papers of P. Koebe, Poincaré and F. Klein; a complete solution was obtained, giving a description of all possible uniformizations of the surface 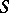 (cf. [4]–[6]). The Klein–Poincaré uniformization theorem (proved in the general case by Poincaré, cf. [2]) states: Every Riemann surface
(cf. [4]–[6]). The Klein–Poincaré uniformization theorem (proved in the general case by Poincaré, cf. [2]) states: Every Riemann surface 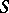 is conformally equivalent to a quotient space
is conformally equivalent to a quotient space 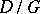 , where
, where 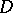 is one of the three canonical domains: the Riemann sphere
is one of the three canonical domains: the Riemann sphere 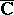 , the complex plane
, the complex plane 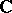 or the unit disc
or the unit disc 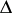 , while
, while 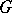 is a properly-discontinuous group of Möbius (fractional-linear) automorphisms of
is a properly-discontinuous group of Möbius (fractional-linear) automorphisms of 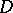 , defined up to conjugation in the group of all Möbius automorphisms of
, defined up to conjugation in the group of all Möbius automorphisms of 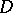 .
.
The cases 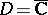 ,
, 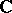 and
and 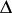 are mutually exclusive. A surface
are mutually exclusive. A surface 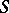 with such a universal holomorphic covering is called elliptic, parabolic or hyperbolic, respectively. Moreover,
with such a universal holomorphic covering is called elliptic, parabolic or hyperbolic, respectively. Moreover, 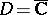 only in the case that
only in the case that 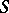 itself is conformally equivalent to
itself is conformally equivalent to 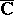 (and so
(and so 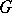 is trivial);
is trivial); 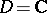 when
when 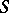 is conformally equivalent to either
is conformally equivalent to either 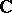 ,
, 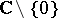 or the torus, and
or the torus, and 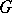 is then either trivial or the group generated by the translation
is then either trivial or the group generated by the translation 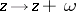 (
(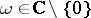 ) or the group generated by the two translations
) or the group generated by the two translations 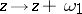 ,
, 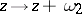 , where
, where  are complex numbers such that
are complex numbers such that 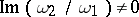 . In the remaining case
. In the remaining case 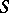 is conformally equivalent to
is conformally equivalent to  , where
, where 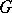 is a torsion-free Fuchsian group. The canonical projection
is a torsion-free Fuchsian group. The canonical projection 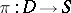 is an unramified covering and uniformizes all functions
is an unramified covering and uniformizes all functions 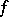 on
on 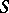 such that
such that  is single-valued on
is single-valued on 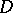 . The Klein–Poincaré theorem also has a generalization to ramified coverings with given order of ramification.
. The Klein–Poincaré theorem also has a generalization to ramified coverings with given order of ramification.
Another approach to the uniformization problem relies on the following principle: If a Riemann surface 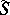 is homeomorphic to a domain
is homeomorphic to a domain 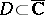 (not necessarily simply connected), then
(not necessarily simply connected), then 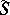 is also conformally equivalent to
is also conformally equivalent to 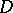 . In the same way the uniformization problem may be reduced to the topological problem of finding all (generally speaking, ramified) flat coverings
. In the same way the uniformization problem may be reduced to the topological problem of finding all (generally speaking, ramified) flat coverings 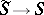 of a given Riemann surface
of a given Riemann surface 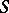 . The solution of this problem is given by the following theorems of Maskit (cf. [4], [5]):
. The solution of this problem is given by the following theorems of Maskit (cf. [4], [5]):
I) Let 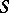 be an oriented surface and let
be an oriented surface and let 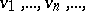 be a set of pairwise disjoint loops on
be a set of pairwise disjoint loops on 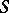 . If
. If 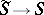 is a regular covering with defining subgroup
is a regular covering with defining subgroup 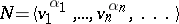 , where
, where 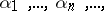 are natural numbers, then
are natural numbers, then 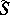 is a flat covering, i.e. is homeomorphic to a domain in
is a flat covering, i.e. is homeomorphic to a domain in 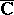 .
.
II) Let 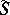 be a flat surface and let
be a flat surface and let 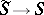 be a regular covering of an oriented surface
be a regular covering of an oriented surface 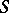 with defining subgroup
with defining subgroup 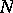 . If
. If  is a surface of finite type, i.e.
is a surface of finite type, i.e. 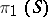 is finitely generated, then there exists a finite set of simple pairwise disjoint loops
is finitely generated, then there exists a finite set of simple pairwise disjoint loops  and natural numbers
and natural numbers  such that
such that 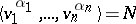 .
.
III) If  is a flat Riemann surface and
is a flat Riemann surface and 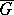 is a properly-discontinuous group of conformal automorphisms of
is a properly-discontinuous group of conformal automorphisms of  , then there exists a conformal homeomorphism
, then there exists a conformal homeomorphism 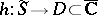 such that
such that  is a Kleinian group with invariant component
is a Kleinian group with invariant component 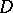 .
.
Thus, every Riemann surface is uniformized by a Kleinian group. E.g., if 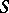 is a closed Riemann surface of genus
is a closed Riemann surface of genus 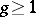 , then its fundamental group has the presentation
, then its fundamental group has the presentation
 |
and the normal subgroup 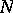 defined by the flat covering
defined by the flat covering 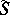 may be taken to be the smallest normal subgroup generated by
may be taken to be the smallest normal subgroup generated by 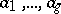 (or
(or 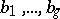 );
); 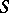 is now uniformized by a Schottky group
is now uniformized by a Schottky group 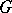 of genus
of genus 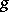 — a free purely-loxodromic Kleinian group with
— a free purely-loxodromic Kleinian group with 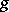 generators (the classical Koebe theorem on cross-cuts).
generators (the classical Koebe theorem on cross-cuts).
In the uniformization of Riemann surfaces of finite type, the possible Kleinian groups may be classified. For this purpose one introduces the notion of a quotient subgroup. If 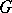 is a Kleinian group with invariant component
is a Kleinian group with invariant component 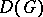 , then a subgroup
, then a subgroup 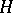 of it is called a quotient subgroup of
of it is called a quotient subgroup of 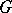 if
if 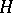 is a maximal subgroup such that: a) its invariant component
is a maximal subgroup such that: a) its invariant component 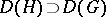 is simply connected; b)
is simply connected; b) 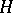 does not contain random parabolic elements (i.e. parabolic elements such that for the conformal isomorphism
does not contain random parabolic elements (i.e. parabolic elements such that for the conformal isomorphism  the image under
the image under 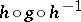 is hyperbolic); and c) every parabolic element of
is hyperbolic); and c) every parabolic element of 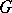 with a fixed point in the limit set of
with a fixed point in the limit set of 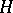 belongs to
belongs to 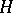 . For example, in the Klein–Poincaré theorem every quotient subgroup of
. For example, in the Klein–Poincaré theorem every quotient subgroup of 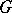 coincides with
coincides with 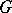 itself, and in Koebe's theorem on cross-cuts all quotient subgroups are trivial. A uniformization
itself, and in Koebe's theorem on cross-cuts all quotient subgroups are trivial. A uniformization 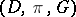 of a Riemann surface
of a Riemann surface  , where
, where 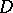 is the invariant component of
is the invariant component of 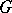 , is called standard if
, is called standard if 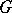 is torsion-free and contains no random parabolic elements. For a closed surface all such uniformizations are described by the following theorem (cf. [6]).
is torsion-free and contains no random parabolic elements. For a closed surface all such uniformizations are described by the following theorem (cf. [6]).
Let 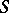 be a closed Riemann surface of genus
be a closed Riemann surface of genus 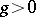 and let
and let 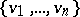 be a set of simple pairwise disjoint loops on
be a set of simple pairwise disjoint loops on 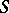 . Then there exists a standard uniformization
. Then there exists a standard uniformization 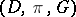 of
of 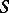 , unique up to conformal equivalence, such that every quotient subgroup
, unique up to conformal equivalence, such that every quotient subgroup 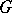 is either Fuchsian or elementary and such that the covering
is either Fuchsian or elementary and such that the covering 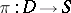 is constructed from the smallest normal subgroup of
is constructed from the smallest normal subgroup of  spanned by the loops
spanned by the loops  .
.
The theory of quasi-conformal mapping and Teichmüller spaces (cf. Teichmüller space) allows one to prove the possibility of simultaneous uniformization of several Riemann surfaces by a single Kleinian group, as well as that of all Riemann surfaces of a given type (cf. [7]).
References
| [1] | F. Klein, "Neue Beiträge zur Riemannschen Funktionentheorie" Math. Ann. , 21 (1883) pp. 141–218 |
| [2] | H. Poincaré, "Sur l'uniformisation des fonctions analytiques" Acta Math. , 31 (1907) pp. 1–64 |
| [3a] | P. Koebe, "Ueber die Uniformisierung beliebiger analytischer Kurven" Nachr. K. Ges. Wissenschaft. Göttinger Math. Phys. Kl. (1907) pp. 191–210 |
| [3b] | P. Koebe, "Ueber die Uniformisierung beliebiger analytischer Kurven II" Nachr. K. Ges. Wissenschaft. Göttinger Math. Phys. Kl. (1907) pp. 177–198 |
| [3c] | P. Koebe, "Ueber die Uniformisierung beliebiger analytischer Kurven III" Nachr. K. Ges. Wissenschaft. Göttinger Math. Phys. Kl. (1908) pp. 337–358 |
| [3d] | P. Koebe, "Ueber die Uniformisierung beliebiger analytischer Kurven IV" Nachr. K. Ges. Wissenschaft. Göttinger Math. Phys. Kl. (1909) pp. 324–361 |
| [4] | B. Maskit, "A theorem on planar covering surfaces with applications to 3-manifolds" Ann. of Math. , 81 : 2 (1965) pp. 341–355 |
| [5] | B. Maskit, "The conformal group of a plane domain" Amer. J. Math. , 90 : 3 (1968) pp. 718–722 |
| [6] | B. Maskit, L.V. Ahlfors (ed.) et al. (ed.) , Contributions to Analysis. Uniformization of Riemann surfaces , Acad. Press (1974) pp. 293–312 |
| [7] | L. Bers, "Uniformization. Moduli and Kleinian groups" Bull. London Math. Soc. , 4 (1972) pp. 257–300 |
| [8] | S.L. Krushkal', B.N. Apanasov, N.A. Gusevskii, "Kleinian groups and uniformization in examples and problems" , Amer. Math. Soc. (1986) (Translated from Russian) |
| [9] | R. Nevanlinna, "Uniformisierung" , Springer (1953) |
| [10] | L.R. Ford, "Automorphic functions" , Chelsea, reprint (1957) |
Comments
References
| [a1] | R.C. Gunning, "On uniformization of complex manifolds: the role of connections" , Princeton Univ. Press (1978) |
| [a2] | G. Springer, "Introduction to Riemann surfaces" , Addison-Wesley (1957) pp. Chapt.10 |
| [a3] | B.N. Apanasov, "Discrete groups in space and uniformization problems" , Kluwer (1991) (Translated from Russian) |
Uniformization. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Uniformization&oldid=13136