Uniform continuity

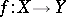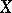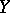A property of a function (mapping) , where and are metric spaces. It requires that for any 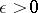there is a 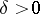such that for all 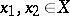satisfying 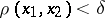, the inequality 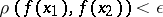holds.

If a mapping 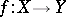is continuous on 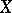and 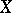is a compactum, then 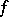is uniformly continuous on 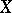. The composite of uniformly-continuous mappings is uniformly continuous.

Uniform continuity of mappings occurs also in the theory of topological groups. For example, a mapping 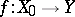, where 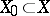, 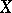and 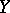topological groups, is said to be uniformly continuous if for any neighbourhood of the identity in 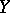, there is a neighbourhood of the identity 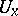in 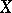such that for any 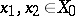satisfying 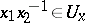(respectively, 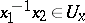), the inclusion 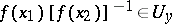(respectively, 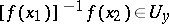) holds.

The notion of uniform continuity has been generalized to mappings of uniform spaces (cf. Uniform space).

References

[1]	A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian)
[2]	L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian)
[3]	J.L. Kelley, "General topology" , Springer (1975)
[4]	N. Bourbaki, "General topology" , Elements of mathematics , Springer (1989) (Translated from French)

Comments

There are several natural uniform structures on a topological group; the (confusing) statement above about uniform continuity of mappings between them can be interpreted in various ways.

References

[a1]	W. Roelcke, S. Dierolf, "Uniform structures on topological groups and their quotients" , McGraw-Hill (1981)
[a2]	R. Engelking, "General topology" , Heldermann (1989)