Berwald space
The Berwald connection  satisfies
satisfies
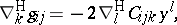 |
where  denotes the so-called Cartan torsion tensor. Clearly,
denotes the so-called Cartan torsion tensor. Clearly,  if and only if
if and only if  is Riemannian (i.e.,
is Riemannian (i.e.,  has no dependence on
has no dependence on  ). So, generally,
). So, generally,  nor is, generally,
nor is, generally,  vanishing.
vanishing.
A Berwald space  is a Finsler manifold (cf. Finsler space) such that its Berwald coefficients
is a Finsler manifold (cf. Finsler space) such that its Berwald coefficients  are independent of
are independent of 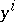 . In fact,
. In fact,  is a Berwald space if and only if
is a Berwald space if and only if  if and only if
if and only if  .
.
Clearly, all Riemannian and locally Minkowski spaces are Berwald spaces (cf. also Riemannian space; Minkowski space). L. Berwald gave a complete characterization of such spaces. He used the frame  and noted that
and noted that
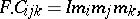 |
where 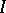 is the so-called principal scalar invariant.
is the so-called principal scalar invariant.
Berwald's theorem, slightly rephrased, reads as follows. If  is a Berwald space which is not locally Minkowski (i.e.,
is a Berwald space which is not locally Minkowski (i.e.,  ), then
), then 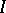 is a constant and
is a constant and 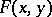 has one of the following four forms:
has one of the following four forms:
1) 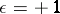 ,
,  :
:
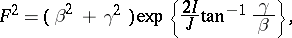 |
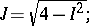 |
2) 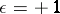 ,
,  :
:
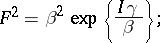 |
3)  ,
, 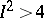 :
:
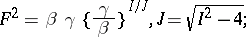 |
4) 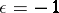 :
:
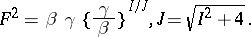 |
Here  and
and 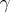 are independent
are independent 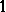 -forms in
-forms in 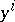 that depend on
that depend on  and where the number
and where the number  equals
equals  if
if  is positive definite and
is positive definite and 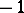 otherwise (cf. also Berwald connection).
otherwise (cf. also Berwald connection).
Applications of Berwald spaces in biology, physics and stochastic processes can be found in [a1], [a2].
References
| [a1] | P.L. Antonelli, R.S. Ingarden, M. Matsumoto, "The theory of sprays and Finsler spaces with applications in physics and biology" , Kluwer Acad. Publ. (1993) |
| [a2] | P.L. Antonelli, T. (eds.) Zastawniak, "Lagrange geometry, Finsler spaces and noise applied in biology and physics" Math. and Comput. Mod. (Special Issue) , 20 (1994) |
Berwald space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Berwald_space&oldid=12731