Euler identity

The relation

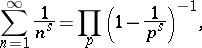where 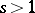is an arbitrary real number and the product extends over all prime numbers 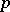. The Euler identity also holds for all complex numbers 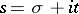with .

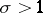The Euler identity can be generalized in the form

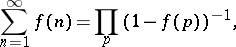which holds for every totally-multiplicative arithmetic function 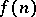for which the series 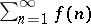is absolutely convergent.

Another generalization of the Euler identity is the formula

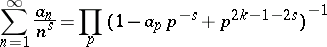for the Dirichlet series

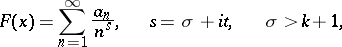corresponding to the modular functions

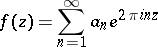of weight 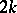, which are the eigen functions of the Hecke operator.

References

[1]	K. Chandrasekharan, "Introduction to analytic number theory" , Springer (1968)
[2]	S. Lang, "Introduction to modular forms" , Springer (1976)

Comments

The product

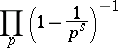is called the Euler product. For Hecke operators in connection with modular forms see Modular form. For totally-multiplicative arithmetic functions cf. Multiplicative arithmetic function.

References

[a1]	E.C. Titchmarsh, "The theory of the Riemann zeta-function" , Clarendon Press (1951)