Topological vector space

over a topological field $ K $

A vector space $ E $ over $ K $ equipped with a topology (cf. Topological structure (topology)) that is compatible with the vector space structure, that is, the following axioms are satisfied: 1) the mapping $ ( x _ {1} , x _ {2} ) \rightarrow x _ {1} + x _ {2} $, $ E \times E \rightarrow E $, is continuous; and 2) the mapping $ ( k, x) \rightarrow kx $, $ K \times E \rightarrow E $, is continuous (here the products $ E \times E $ and $ K \times E $ are thought of as having the product topologies). Entirely analogously, one can define topological left and right vector spaces over a (not necessarily commutative) topological division ring. Sometimes a topological vector space $ E $ with a topology $ \tau $ is denoted by $ ( E, \tau ) $. On the other hand, reference to the field $ K $ is often not made.

Two topological vector spaces $ E _ {1} $ and $ E _ {2} $ over the same topological field are said to be isomorphic if there exists a continuous bijective linear transformation from $ E _ {1} $ onto $ E _ {2} $ whose inverse is also continuous. The dimension of a topological vector space $ ( E, \tau ) $ is the dimension of the vector space $ E $.

Methods for specifying a topology in a topological vector space, and properties of the topology.

Let $ ( E, \tau ) $ be a topological vector space over a topological field $ K $. The topology $ \tau $ is invariant under translations (that is, for any $ a \in E $ the mapping $ x \rightarrow x + a $ is a homeomorphism from $ E $ onto itself). Hence the topology $ \tau $ is uniquely determined by a base (basis, fundamental system) of neighbourhoods of any fixed point (in particular, of zero). The topology $ \tau $ is compatible with the additive group structure of $ E $, and the following propositions hold. 1) $ E $ is Hausdorff (separated) if and only if, for every point $ x \neq 0 $ of $ E $, there exists a neighbourhood of zero which does not contain $ x $. 2) If $ E $ is Hausdorff, then it is completely regular. 3) There exists a unique uniform structure (cf. also Uniform space) on $ E $ with the following properties: a) it is invariant under translations (that is, all translations are uniformly continuous); and b) the topology associated with it coincides with the original topology of the space $ E $. A set in a topological vector space is called complete if it is complete with respect to the above-mentioned uniform structure. Thus, a topological vector space $ E $ is complete if every Cauchy filter in $ E $ converges. For every topological vector space $ E $ there exists a complete topological vector space, over the same field, containing $ E $ as an everywhere-dense subset and inducing the original topology and linear structure on $ E $. It is called the completion of $ E $. Every Hausdorff topological vector space has a Hausdorff completion, unique up to an isomorphism fixing $ E $ pointwise.

From now on, unless explicitly stated otherwise, $ K $ will be assumed to be a non-discretely normed field equipped with the topology induced by the norm (cf. Norm on a field). If $ E $ is a vector space over $ K $, then a set $ Q \subset E $ is called circled (or balanced) if $ kQ \subset Q $ for all $ k \in K $ with $ | k | \leq 1 $. If $ A $ and $ B $ are two subsets of $ E $, then one says that $ A $ absorbs $ B $ if there exists a positive number $ r $ such that $ kA \supset B $ for all $ k \in K $ with $ | k | \geq r $. A subset of $ E $ is called absorbing (or radial) if it absorbs every one point set. In every topological vector space $ E $ over $ K $ there exists a base $ {\mathcal U} $ of closed neighbourhoods of zero with the following properties: $ \alpha $) for every set $ V \in {\mathcal U} $ there exists a $ W \in {\mathcal U} $ such that $ W + W \subset V $; $ \beta $) every $ V \in {\mathcal U} $ is a balanced absorbing set; and $ \gamma $) if $ V \in {\mathcal U} $, then $ kV \in {\mathcal U} $ for every $ k \neq 0 $ in $ K $. On the other hand, let $ \tau $ be a topology on a vector space $ E $ over $ K $ which is invariant under translations and has a base of neighbourhoods of zero satisfying properties $ \alpha $) and $ \beta $), and also the following property: $ \gamma _ {1} $) there exists a $ k \in K $, $ 0 < | k | < 1 $, such that if $ V \in {\mathcal U} $, then $ kV \in {\mathcal U} $. Then $ E $, together with the topology $ \tau $, is a topological vector space over $ K $( in case the norm on $ K $ is Archimedean (cf. Archimedean axiom), $ \gamma _ {1} $) is a consequence of the other properties imposed on $ ( E, \tau ) $). Every filter base $ {\mathcal U} $ in a vector space $ E $ over $ K $ which satisfies properties $ \alpha $), $ \beta $) and $ \gamma _ {1} $), or at least $ \alpha $) and $ \beta $) in the case of a field with an Archimedean norm, is a fundamental system of neighbourhoods of zero (not necessarily closed) for some uniquely determined topology $ \tau $ on $ E $ that is compatible with the vector-space structure on $ E $. A topological vector space $ E $ over the field $ \mathbf R $ of real numbers or the field $ \mathbf C $ of complex numbers, and its topology, are called locally convex if $ E $ has a base of neighbourhoods of zero consisting of convex sets (the definition of a locally convex space sometimes requires also that the space be Hausdorff).

Examples.

1) Every topological field $ K $ can be thought of as a (one-dimensional) topological vector space over itself. Considered in this way, it will be denoted by $ K _ {0} $.

2) Let $ I $ be a non-empty set, and let $ K _ {0} ^ {I} $ be the vector space over $ K $ which is the product of $ I $ copies of $ K _ {0} $, equipped with the product topology. Then $ K _ {0} ^ {I} $ is a topological vector space.

3) If the topology of the topological field $ K $ is discrete, then every vector space $ E $ over $ K $, with a topology that is compatible with its additive group structure and that is invariant under multiplication by any non-zero element of $ K $, is a topological vector space (these conditions are satisfied, in particular, by the discrete topology on $ E $). A topological vector space over a field with the discrete topology is called a topological vector group.

4) Let $ E $ be a vector space over the topological field $ K $, and let $ {\mathcal P} $ be a set of semi-norms on $ E $. The ball of radius $ r > 0 $ in the semi-norm $ p $ on $ E $ is the set $ \{ {x \in E } : {p ( x) < r } \} $. The set of all intersections of finite collections of balls (of all (positive) radii) in (all) semi-norms belonging to $ {\mathcal P} $, forms a base of neighbourhoods of zero for a certain topology $ \tau _ {\mathcal P} $ on $ E $ that is compatible with the vector-space structure. One says that this topology is given, or defined, by $ {\mathcal P} $. If $ K = \mathbf R $ or $ K = \mathbf C $, then $ \tau _ {\mathcal P} $ is locally convex. Conversely, the topology of any locally convex space can be defined by some set of semi-norms — for example, by the set of gauge functions (Minkowski functionals) of an arbitrary subbase of neighbourhoods of zero consisting of balanced convex sets.

A subset of a topological vector space is called bounded if it is absorbed by every neighbourhood of zero.

A topological vector space is called normable if its topology can be defined by a single norm. A topological vector space over $ \mathbf R $ or $ \mathbf C $ is normable if and only if it is Hausdorff and has a convex bounded neighbourhood of zero (Kolmogorov's theorem).

5) Let $ n $ be a natural number, let $ I _ {n} $ be a set containing $ n $ elements and let $ K _ {0} ^ {n} = K _ {0} ^ {I _ {n} } $. The topology of $ K _ {0} ^ {n} $ is defined by the norm $ \| x \| = \sum _ {i = 1 } ^ {n} | x _ {i} | $, where the symbol $ | \cdot | $ denotes the norm in $ K $. If the field $ K $ is complete, then every $ n $- dimensional topological vector space over $ K $ is isomorphic to $ K _ {0} ^ {n} $( for $ n = 1 $ this holds even without the completeness assumption on $ K $). If the field $ K $ is locally compact, then a Hausdorff topological vector space over $ K $ is finite dimensional if and only if it has a pre-compact neighbourhood of zero (Tikhonov's theorem).

A topological vector space is called metrizable if its topology can be defined by some metric (among all such metrics, there always exists one that is invariant under translations). A topological vector space is metrizable if and only if it is Hausdorff and has a countable base of neighbourhoods of zero.

6) Let $ ( E, \tau ) $ be a topological vector space, let $ E _ {1} $ be a vector subspace of $ E $ and let $ \tau _ {1} $ be the subspace topology on $ E _ {1} $. The topology $ \tau _ {1} $ is compatible with the vector-space structure of $ E _ {1} $. The topological vector space $ ( E _ {1} , \tau _ {1} ) $ is called a topological vector subspace of the topological vector space $ ( E, \tau ) $. If $ {\mathcal U} $ is a base (respectively, subbase) of neighbourhoods of zero in $ ( E, \tau ) $, then the set $ \{ {V \cap E _ {1} } : {V \in {\mathcal U} } \} $ forms a base (respectively, subbase) of neighbourhoods of zero in $ ( E _ {1} , \tau _ {1} ) $. If $ ( E, \tau ) $ is Hausdorff (respectively, metrizable, locally convex), then so is $ ( E _ {1} , \tau _ {1} ) $. If the topology $ \tau $ is given by some set of semi-norms, then the topology $ \tau _ {1} $ is given by the restrictions of these semi-norms to $ E _ {1} $.

7) Let $ ( E, \tau ) $ and $ E _ {1} $ be as in 6) above, and let $ E/E _ {1} $ be the quotient vector space of $ E $ by the subspace $ E _ {1} $. The quotient topology $ \tau _ {2} $ on $ E/E _ {1} $ is compatible with the vector-space structure on $ E/E _ {1} $. The topological vector space $ ( E/E _ {1} , \tau _ {2} ) $ is called the topological vector quotient space of $ ( E, \tau ) $ over $ E _ {1} $. (By the definition of a quotient space, a set $ V \subset E/E _ {1} $ is closed in $ \tau _ {2} $ if and only if its inverse image under the canonical mapping $ E \rightarrow E/E _ {1} $ is closed in $ ( E, \tau ) $.) If $ {\mathcal U} $ is a base of neighbourhoods of zero in $ E $, then the set of images of its elements under the canonical mapping $ E \rightarrow E/E _ {1} $ forms a base of neighbourhoods of zero in $ ( E/E _ {1} , \tau _ {2} ) $( for a subbase, this does not hold in general). The topological vector space $ ( E/E _ {1} , \tau _ {2} ) $ is Hausdorff if and only if the subspace $ E _ {1} $ is closed in $ ( E, \tau ) $. If $ \overline{ {\{ 0 \} }}\; $ denotes the closure of the singleton set $ \{ 0 \} $ in $ ( E, \tau ) $, then the (Hausdorff) topological vector space $ E/ \overline{ {\{ 0 \} }}\; $ is called the Hausdorff topological vector space associated with $ E $. Of course, if $ E $ itself is Hausdorff, then the associated Hausdorff topological vector space is isomorphic to it. If $ E $ is locally convex (respectively, if $ E $ is metrizable and $ E _ {1} $ is closed; or if $ E $ is metrizable and complete), then $ E/E _ {1} $ is locally convex (respectively, metrizable, complete). However, $ E $ can be complete (non-metrizable) and have a non-complete topological vector quotient (even a separable metrizable one) (see below).

8) Let $ {\mathcal F} $ be the vector space of all Lebesgue-measurable real-valued functions on $ [ 0, 1] $, let $ \mu _ {l} $ be the Lebesgue measure on this interval and, for each $ n \in \mathbf Z _ {+} $, let

$$ V _ {n} = \ \left \{ {f \in {\mathcal F} } : { \mu _ {l} \left \{ t \in [ 0, 1] : | f ( t) | > { \frac{1}{n + 1 } } } \right \} < \ { \frac{1}{n + 1 } } \right \} . $$

The set $ {\mathcal U} = \{ {V _ {n} } : {n \in \mathbf N } \} $ forms a filter base in $ {\mathcal F} $ with the properties $ \alpha $) and $ \beta $). Let $ \tau $ be the topology compatible with the vector-space structure on $ {\mathcal F} $ with base of neighbourhoods of zero $ {\mathcal U} $, and let $ {\mathcal F} _ {0} $ be the Hausdorff topological vector space associated with $ ( {\mathcal F} , \tau ) $( $ ( {\mathcal F} , \tau ) $ itself is not Hausdorff). The topological vector space $ {\mathcal F} _ {0} $ is metrizable, but not locally convex. As a vector space, it can be identified with the space of $ \mu _ {l} $- equivalence classes of $ \mu _ {l} $- measurable real-valued functions on $ [ 0, 1] $. Convergence of a sequence in $ ( {\mathcal F} , \tau ) $( respectively, $ {\mathcal F} _ {0} $) is the same as convergence in measure (of individual functions in the first case, and of $ \mu _ {l} $- equivalence classes in the second).

From now on $ K = \mathbf R $ or $ K = \mathbf C $.

9) Let $ S = S ( \mathbf R ^ {n} ) $ be the vector space of all infinitely-differentiable functions $ \phi $ on $ \mathbf R ^ {n} $, with values in $ K $, for which $ ( t = ( t _ {1} \dots t _ {n} ) \in \mathbf R ^ {n} ) $: For all $ k, r \in \mathbf Z _ {+} $,

$$ p _ {rk} ( \phi ) \equiv \ \max ( 1 + \| t \| ^ {r} ) \| \phi ^ {(} k) ( t) \| < \infty , $$

where

$$ \| t \| = \ \left ( \sum | t _ {i} | ^ {2} \right ) ^ {1/2} , $$

$$ \| \phi ^ {(} k) ( t) \| = \max \left \{ \left | \frac{\partial ^ {k} \phi ( t) }{\partial t _ {1} ^ {k _ {1} } \dots \partial _ {t _ {n} } ^ {k _ {n} } } \right | : k _ {1} + \dots + k _ {n} = k \right \} . $$

Endowed with the topology $ \tau _ {S} $ given by the collection of norms $ p _ {rk} $ defined by the above equations, $ S $ is a complete, metrizable, locally convex space (such spaces are called Fréchet spaces). The space $ ( S, \tau _ {S} ) $ plays an important part in the theory of generalized functions (cf. Generalized function). It is interesting that there is no norm on $ S $ for which $ S $ is a Banach space and in which the functions $ \phi \mapsto \phi ( t) $, $ S \rightarrow K $( $ t \in \mathbf R $), are all continuous (in particular, $ ( S, \tau _ {S} ) $ is not normable).

Some methods for constructing topological vector spaces.

1) Projective topologies. Let $ E $ be a vector space, and for each $ \alpha $ in some index set $ \mathfrak A $, let $ g _ \alpha $ be a linear transformation from $ E $ into a topological vector space $ E _ \alpha $. Then among all the topologies on $ E $ for which all mappings $ g _ \alpha $ are continuous, there is a weakest one $ \tau $( the supremum of the set of topologies $ \{ {g _ \alpha ^ {-} 1 ( \tau _ \alpha ) } : {\alpha \in A } \} $, where $ \tau _ \alpha $ is the topology on $ E _ \alpha $ for each $ \alpha $). The topology $ \tau $ is called a projective topology, and the space $ E $ endowed with $ \tau $ is called the projective limit of the collection of spaces $ E _ \alpha $ with respect to the mappings $ g _ \alpha $. The topology $ \tau $ is compatible with the vector-space structure on $ E $, and if all spaces $ ( E _ \alpha , \tau _ \alpha ) $ are locally convex, then so is $ ( E, \tau ) $. (Sometimes the term "projective limit" is used to denote a more special construction, and not as a synonym for "space with a projective topology" , cf. Locally convex space.)

Examples of projective limits.

a) The product of a collection of spaces $ E _ \alpha $ endowed with the projective topology with respect to the projections $ g _ \alpha $— hence the term "projective limit" .

b) Let $ E $ be a vector space and let $ \{ \tau _ \alpha \} $ be a collection of topologies on $ E $ compatible with its vector-space structure. The space $ E $ endowed with the supremum of the topologies $ \{ \tau _ \alpha \} $ is the projective limit of the collection of topological vector spaces $ \{ ( E, \tau _ \alpha ) \} $ with respect to the collection of identity mappings $ E \rightarrow E $.

c) A topological vector subspace $ E _ {1} $ of $ E $ is the projective limit of the singleton collection $ \{ E \} $ with respect to the inclusion mapping $ E _ {1} \rightarrow E $.

d) Any locally convex space is the projective limit of a collection of Banach spaces (cf. Banach space).

2) Inductive topologies. Let $ E $ be a vector space, and for each $ \alpha $ in some set $ \mathfrak A $, let $ g _ \alpha $ be a linear transformation from a topological vector space $ E _ \alpha $ into $ E $. Then in $ E $ there exist: a) a strongest topology in which all $ g _ \alpha $ are continuous; b) a strongest topology compatible with the vector-space structure in which all these mappings are continuous; c) a strongest locally convex topology in which all $ g _ \alpha $ are continuous (even in the case that all $ E _ \alpha $ are locally convex spaces, these three topologies may be distinct). If all $ E _ \alpha $ are locally convex spaces, then the space $ E $ endowed with the topology defined in c) is called the inductive limit of the collection $ \{ E _ \alpha \} $ with respect to the mappings $ g _ \alpha $, and the topology is an inductive topology (of the same collection with respect to the same mappings). The term "inductive limit" is sometimes used in different senses. That introduced here is the widest which occurs in the literature. An inductive topology is a projective topology, being the supremum of a collection of topologies.

Examples of inductive limits: a) The locally convex direct sum of a collection $ \{ E _ \alpha \} $ of locally convex spaces. This is the algebraic direct sum $ E $ of the collection of vector spaces $ \{ E _ \alpha \} $, endowed with the inductive topology of the collection of locally convex spaces $ \{ E _ \alpha \} $ with respect to the collection of canonical inclusions $ g _ \alpha $ of $ E _ \alpha $ into $ E $. b) Let $ E $ be a vector space and let $ \{ \tau _ \alpha \} $ be a collection of locally convex topologies on $ E $ that are compatible with the vector-space structure. Let $ \tau $ be its infimum in the class of all locally convex topologies. Then the locally convex space $ ( E, \tau ) $ is the inductive limit of the collection of locally convex spaces $ \{ ( E, \tau _ \alpha ) \} $ with respect to the collection of identity mappings on $ E $. c) Let $ E $ be a locally convex space and let $ E _ {1} $ be a vector subspace. The topological vector quotient space $ E/E _ {1} $ is the inductive limit of the singleton collection $ \{ E \} $ with respect to the canonical mapping $ E \rightarrow E/E _ {1} $. d) A locally convex space is called bornological if any linear transformation from it into any Banach space which maps every bounded set to a bounded set, is continuous. A locally convex space is bornological if and only if it is the inductive limit of a collection of normable, locally convex spaces. e) Let $ \Omega $ be a non-empty open subset of the space $ \mathbf R ^ {n} $, and for every compactum $ K \subset \Omega $, let $ D _ {K} $ be the topological vector subspace of $ ( S ( \mathbf R ^ {n} ), \tau _ {S} ) $ consisting of all functions in $ S ( \mathbf R ^ {n} ) $ that vanish on $ \Omega \setminus K $. Let $ D ( \Omega ) $ be the vector subspace $ \cup \{ {D _ {K} } : {K \subset \Omega } \} $ endowed with the inductive topology of the collection of locally convex spaces $ \{ {D _ {K} } : {K \subset \Omega } \} $ with respect to the canonical inclusions $ D _ {K} \rightarrow D \subset ( \Omega ) $. The locally convex space $ D ( \Omega ) $( which also plays an important part in the theory of generalized functions) is complete, Hausdorff and non-metrizable. It is a Montel space, hence paracompact, and so normal. The space $ D ( \Omega ) $ has a non-complete metrizable quotient space [11] which is a proper dense subspace of some $ \mathbf R ^ {N} $.

3) Spaces of mappings. Let $ E $ be a topological vector space, $ T $ a set and $ \sigma $ a set of subsets of $ T $ ordered by inclusion, so that the following property holds: for all $ B _ {1} , B _ {2} \in \sigma $ there exists a $ B _ {3} \in \sigma $ with $ B _ {3} \supset B _ {1} \cup B _ {2} $. Let $ L $ be some vector space of mappings from $ T $ into $ E $( with the natural algebraic operations), and let $ {\mathcal U} $ be a base of neighbourhoods of zero in $ E $. For $ B \in \sigma $ and $ V \in {\mathcal U} $, let $ v _ {B; V } = \{ {g \in L } : {g ( B) \subset V } \} $. Then the set $ \{ {v _ {B; V } } : {B \in \sigma, V \in {\mathcal U} } \} $ is a base of neighbourhoods of zero (the mapping $ f \in L $ that maps the whole of $ T $ to the zero element of $ E $) for a unique topology on $ L $ that is invariant under translations. This topology is called the topology of uniform convergence on sets in $ \sigma $, or the $ \sigma $- topology for short. This topology is compatible with the vector-space structure on $ L $ if and only if the set $ f ( B) $ is bounded in $ E $ for all $ f \in L $ and all $ B \in \sigma $. This holds, e.g., if $ \sigma $ is the set of all finite subsets of $ T $. In this case the $ \sigma $- topology on $ L $ is called the topology of pointwise convergence. This topology is the projective topology (in $ L $) of a collection $ \{ {E _ {t} } : {t \in T } \} $ consisting of copies of the space $ E $, with respect to the mappings $ L \rightarrow E _ {t} $, $ g \rightarrow g ( t) $. The space $ L $ endowed with the $ \sigma $- topology will be denoted by $ L _ \sigma $. If $ T $ is a topological vector space and if all the elements of the space $ L $ are continuous linear mappings and all the elements of $ \sigma $ are bounded sets in $ T $, then $ L _ \sigma $ is also a topological vector space. If $ E $ is a locally convex space, then so is $ L _ \sigma $. The vector space of all continuous linear mappings from a topological vector space $ E _ {1} $ into $ E _ {2} $ is denoted by $ {\mathcal L} ( E _ {1} , E _ {2} ) $. In particular, suppose that $ E $ is a locally convex space. The (topologically) dual space to $ E $ is the vector space $ E ^ \prime $ of all continuous linear functionals on $ E $. Thus $ E ^ \prime = {\mathcal L} ( E, K _ {0} ) $. Endowed with the topology of uniform convergence on the set $ \beta $ of all bounded subsets of $ E $, it is called the strong dual (and its topology is called the strong topology), and is denoted by $ \beta ( E ^ \prime , E) $. The topology of pointwise convergence on $ E ^ \prime $ is also called the weak topology, or, more often, the weak- $ * $ topology. The generally accepted notation for the weak- $ * $ topology is $ \sigma ( E ^ \prime , E) $. It is known that the topological dual space of $ E _ \sigma ^ \prime $ can be canonically identified with $ E $ in the obvious manner $ ( E \ni x \mapsto [ g \mapsto g( x) ]) $. Hence $ E $ can be given the topology $ \sigma ( E , E ^ \prime ) $ of pointwise convergence on $ E ^ \prime $( called the weak topology). $ ( E, \sigma ( E, E ^ \prime )) $ is often denoted by $ E _ \sigma $. Its dual is $ E ^ \prime $ and, moreover, $ \sigma ( E , E ^ \prime ) $ is the weakest locally convex topology $ \tau $ on $ E $ such that $ ( E , \tau ) ^ \prime = E ^ \prime $. There is also a strongest locally convex topology with this property, the so-called Mackey topology $ \mu ( E, E ^ \prime ) $. The Mackey topology is the topology of uniform convergence on the absolutely convex $ \sigma ( E ^ \prime , E) $- compact subsets of $ E ^ \prime $. When $ E $ is a normed space, $ \sigma ( E ^ \prime , E ) $ is called the weak $ {} ^ {*} $ topology on $ E ^ \prime $. The topology of any locally convex space can be considered as the topology of convergence on some set of subsets of the dual space.

4) Tensor products. Let $ E _ {1} $ and $ E _ {2} $ be locally convex spaces, let $ E _ {1} \otimes E _ {2} $ be their algebraic tensor product, and let $ b $ be the canonical bilinear mapping from the topological space $ E _ {1} \times E _ {2} $ into $ E _ {1} \otimes E _ {2} $. The projective (respectively, inductive) topology on $ E _ {1} \otimes E _ {2} $ is the strongest of all locally convex topologies on $ E _ {1} \otimes E _ {2} $ such that $ b $ is continuous (respectively, separately continuous). Although this terminology is not completely consistent, it is generally accepted. The locally convex space obtained by putting the projective (respectively, injective) topology on the vector space $ E _ {1} \otimes E _ {2} $ is denoted by $ E _ {1} \otimes _ \pi E _ {2} $( $ E _ {1} \otimes _ {i} E _ {2} $) and its completion by $ E _ {1} \widehat \otimes _ \pi E _ {2} $( $ E _ {1} \widehat \otimes _ {i} E _ {2} $). The spaces $ E _ {1} \otimes _ \pi E _ {2} $ and $ E _ {1} \otimes _ {i} E _ {2} $ are called the locally convex tensor products of the corresponding locally convex spaces, and their completions are called the complete locally convex tensor products. There exist other locally convex tensor products besides those introduced here. These arise by introducing on the algebraic tensor product topologies other than those described above. Many of the properties of tensor products are simpler if one of the factors is a nuclear space.

Examples. The locally convex spaces $ S ( \mathbf R ^ {n} ) \widehat \otimes _ \pi S ( \mathbf R ^ {k} ) $, $ S ( \mathbf R ^ {n} ) \widehat \otimes _ {i} S ( \mathbf R ^ {k} ) $ and $ S ( \mathbf R ^ {n + k } ) $ are canonically isomorphic (the isomorphism between the first two is a consequence of the fact that every separately-continuous bilinear mapping from a product of Fréchet spaces into an arbitrary locally convex space is continuous). The locally convex spaces $ D ( \mathbf R ^ {n} ) \widehat \otimes _ {i} D ( \mathbf R ^ {k} ) $ and $ D ( \mathbf R ^ {n + k } ) $ are also canonically isomorphic. The vector spaces $ D ( \mathbf R ^ {n} ) \widehat \otimes _ \pi D ( \mathbf R ^ {k} ) $ and $ D ( \mathbf R ^ {n + k } ) $ are canonically isomorphic, but their topologies do not coincide , [9].

Duality.

An important part in the study of locally convex spaces is played by the relation between a locally convex space and its dual. In particular, certain properties of a locally convex space depend only on the size of the dual space. Thus, if $ E $ is a locally convex space and $ E ^ \prime $ is its dual, then for all locally convex topologies on $ E $ that are compatible with the duality between $ E $ and $ E ^ \prime $, the bounded sets are precisely the same, and the closed convex sets are also precisely the same.

Duality theory turns out to be useful in the study of complete spaces. Thus, a locally convex space (respectively, metrizable locally convex space) $ E $ is complete if and only if every hyperplane (respectively, convex subset) of its dual $ E ^ \prime $ whose intersections with the polars of all neighbourhoods of zero in $ E $ are all closed in the topology $ \sigma ( E ^ \prime , E) $, is itself closed in that topology (Banach–Grothendieck and Krein–Shmul'yan theorems).

In this context one can make the following definition. A locally convex space is called $ B _ {r} $- complete (respectively, $ B $- complete or fully complete, hypercomplete, a Krein–Shmul'yan space) if any everywhere-dense linear subspace (respectively, linear subspace, absolutely-convex subset, convex subset) of $ ( E ^ \prime , \sigma ( E ^ \prime , E)) $ whose intersections with the polars of all neighbourhoods of zero in $ E $ are closed, is itself closed. These classes of spaces play an important part in generalizations of Banach's closed-graph and open-mapping theorems (cf. below). Complete, metrizable, locally convex spaces, and strong duals of reflexive (cf. below), metrizable, locally convex spaces, belong to each of these classes. At the same time the spaces $ D $ and $ D ^ \prime $ do not belong to any of them. The classes of hypercomplete spaces and Krein–Shmul'yan spaces do not coincide. However, it is not yet known (1992) whether or not the classes of $ B _ {r} $- complete spaces and hypercomplete spaces coincide.

Using duality methods, one can also prove the following propositions about the compact subsets of locally convex spaces. 1) Let $ E $ be a locally convex space and let $ H $ be a subset of $ E $ with a complete closed convex hull in the Mackey topology. If every sequence of elements of $ H $ has a limit point in $ E $, then $ H $ is relatively compact (Eberlein's theorem). 2) Let $ E $ be a metrizable locally convex space and let $ \{ x _ {n} \} $ be a sequence in $ E $ for which every subsequence has a limit point in $ ( E, \sigma ( E, E ^ \prime )) $. Then one can extract a convergent subsequence from $ \{ x _ {n} \} $( Shmul'yan's theorem). 3) Let $ B $ be a compact subset of a Hausdorff locally convex space $ E $ and let $ C $ be the closed convex hull of $ B $. Then $ C $ is compact if and only if it is complete in the Mackey topology (Krein's theorem).

A locally convex space $ E $ is called semi-reflexive (respectively, reflexive) if the canonical inclusion $ x \rightarrow [ g \rightarrow g ( x)] $, $ E \rightarrow ( E _ \beta ^ \prime ) _ \beta ^ \prime $, is an isomorphism of vector spaces (respectively, an isomorphism of topological vector spaces). A locally convex space $ E $ is semi-reflexive if and only if every bounded subset in it is relatively compact in the topology $ \sigma ( E, E ^ \prime ) $. It is reflexive if and only if it is a semi-reflexive barrelled space.

Mappings between topological vector spaces.

1) Closed-graph and open-mapping theorems. A linear mapping $ f $ from a topological vector space $ E _ {1} $ into a topological vector space $ E _ {2} $ is called a topological homomorphism if it maps every open set in $ E _ {1} $ to an open set in $ f ( E _ {1} ) $( in the topology induced from that of $ E _ {2} $). The graph of $ f: E _ {1} \rightarrow E _ {2} $ is the set $ \{ {( x, f ( x)) } : {x \in E _ {1} } \} \subset E _ {1} \times E _ {2} $.

Let $ {\mathcal E} _ {1} $ and $ {\mathcal E} _ {2} $ be two classes of topological vector spaces. One says that the closed-graph theorem (respectively, the homomorphism or open-mapping theorem) holds for the pair $ ( {\mathcal E} _ {1} , {\mathcal E} _ {2} ) $ if for all $ E _ {1} \in {\mathcal E} _ {1} $ and $ E _ {2} \in {\mathcal E} _ {2} $, every linear mapping $ f: E _ {1} \rightarrow E _ {2} $ whose graph is closed in the topological vector space $ E _ {1} \times E _ {2} $ is continuous (respectively, if every surjective continuous linear mapping from $ E _ {2} $ onto $ E _ {1} $ is a topological homomorphism). If $ {\mathcal E} $ is the class of all complete, metrizable, topological vector spaces, then both the closed-graph theorem and the open-mapping theorem hold for $ ( {\mathcal E} , {\mathcal E} ) $( Banach's theorem). This result can be strengthened: Let $ {\mathcal E} _ {1} $ be the class of all Hausdorff locally convex spaces which are inductive limits of families of Banach spaces (such spaces are called ultrabornological), and let $ {\mathcal E} _ {2} $ be the smallest class of locally convex spaces that contains all complete, metrizable, locally convex spaces and that is closed with respect to projective and inductive limits of countable collections of spaces in it. Then the closed-graph and open-mapping theorems hold for the pair $ ( {\mathcal E} _ {1} , {\mathcal E} _ {2} ) $( Raikov's theorem). (All the complete locally convex spaces arising in functional analysis, with their usual topologies, belong to both of these classes.) In fact, the assertion formulated can be proved for a somewhat wider class $ {\mathcal E} _ {2} ^ \prime $ of topological vector spaces than $ {\mathcal E} _ {2} $, and for multi-valued linear mappings. In [7] yet another class $ {\mathcal E} _ {2} ^ {\prime\prime} \supset {\mathcal E} _ {2} ^ \prime $ of topological vector spaces has been described that can play the part of $ {\mathcal E} _ {2} $ in the assertion — the so-called spaces with a web.

Let $ {\mathcal E} $, $ {\mathcal E} _ {\mathcal P} $, $ {\mathcal E} _ {\mathcal P} ^ {r} $ be, respectively, the class of all Hausdorff barrelled, totally complete, and $ B _ {r} $- complete, locally convex spaces. Then the closed-graph theorem holds for $ ( {\mathcal E} , {\mathcal E} _ {\mathcal P} ^ {r} ) $, and the open-mapping theorem holds for $ ( {\mathcal E} , {\mathcal E} _ {\mathcal P} ) $.

2) Fixed-point theorems. a) Let $ E $ be a Hausdorff locally convex space, let $ K $ be a non-empty convex compact subset of it and let $ f $ be a mapping from $ K $ into the set of non-empty convex closed subsets of $ K $. Suppose that for each $ x \in K $ and each neighbourhood $ {\mathcal U} $ of the set $ f ( x) $, there exists a neighbourhood $ {\mathcal V} $ of $ x $ such that $ f ( {\mathcal V} \cap K) \subset {\mathcal U} $( this property of $ f $ is called upper semicontinuity). Then there exists a point $ z \in K $ such that $ z \in f ( z) $— a "fixed point" of $ f $( Fan's theorem — a generalization of the Schauder–Tikhonov theorem). b) Let $ E $ be a Hausdorff topological vector space, let $ K $ be a non-empty, compact, convex subset of it, and let $ \Gamma $ be a set of pairwise-commuting continuous mappings $ g $ from $ K $ into $ K $ with the following property: If $ x, z \in K $ and $ \alpha , \beta \in \mathbf R $ with $ \alpha , \beta > 0 $ and $ \alpha + \beta = 1 $, then $ g ( \alpha x + \beta z) = \alpha g ( x) + \beta g ( z) $. Then there exists a point $ z _ {0} \in K $ such that $ g ( z _ {0} ) = z _ {0} $ for all $ g \in \Gamma $( the Markov–Kakutani theorem).

3) Also of great importance in the theory of locally convex spaces are the Hahn–Banach theorem and the Banach–Steinhaus theorem.

A number of interesting results in the theory of measures taking values in locally convex spaces and, (especially) in connection with the theory of random processes, in the theory of numerical cylindrical measures on locally convex spaces, have been obtained.

Mathematical analysis on topological vector spaces has arisen, and continues to develop — so-called infinite-dimensional analysis. Although a generalization of classical analysis, it also differs from it, both in terms of the problems and results which arise and in terms of the methods. Infinite-dimensional analysis includes the theory of differentiable mappings on topological vector spaces and differentiable measures on topological vector spaces; the theory of generalized functions and measures (distributions) on topological vector spaces; and the theory of differential equations — both with respect to functions of a real argument and taking values in a topological vector space, and with respect to numerical functions and measures (possibly generalized) defined on a topological vector space. The language of infinite-dimensional analysis is very natural for the formulation of fundamental problems in the physics of infinite-dimensional systems — quantum field theory, statistical mechanics and hydrodynamics — as well as of certain mathematical problems originating outside infinite-dimensional analysis.

References

[1]	N. Bourbaki, "Elements of mathematics. Topological vector spaces" , Addison-Wesley (1977) (Translated from French)
[2]	A.P. Robertson, W.S. Robertson, "Topological vector spaces" , Cambridge Univ. Press (1964)
[3]	H.H. Schaefer, "Topological vector spaces" , Macmillan (1966)
[4]	R.E. Edwards, "Functional analysis: theory and applications" , Holt, Rinehart & Winston (1965)
[5]	A. Pietsch, "Nuclear locally convex spaces" , Springer (1972) (Translated from German)
[6]	A. Pietsch, "Operator ideals" , Deutsch. Verlag Wissenschaft. (1978)
[7]	M. de Wilde, "Closed graph theorems and webbed spaces" , Pitman (1978)
[8a]	L. Schwartz, "Théorie des distributions" , 1–2 , Hermann (1966)
[8b]	L. Schwartz, "Théorie des distributions à valeurs vectorielles I" Ann. Inst. Fourier (Grenoble) , 7 (1957) pp. 1–141
[8c]	L. Schwartz, "Théorie des distributions à valeurs vectorielles II" Ann. Inst. Fourier (Grenoble) , 8 (1958) pp. 1–209
[9]	E.T. Shavgulidze, "Conditions for certain forms of completeness in the class of projective limits of sequences of inductive limits of sequences of Fréchet spaces" Funct. Anal. Appl. , 11 : 1 (1972) pp. 82–83 Funkts. Anal. i Prilozhen. , 11 : 1 (1977) pp. 91–92
[10]	O.G. Smolyanov, "The space 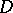is not hereditarily complete" Math. USSR Izv. , 5 : 3 (1971) pp. 696710 Izv. Akad. Nauk SSSR, Ser. Mat. , 35 : 3 (1971) pp. 682–696
[11]	O.G. Smolyanov, "Analysis on topological linear spaces and applications" , Moscow (1979) (In Russian)
[12]	H. Jarchow, "Locally convex spaces" , Teubner (1981) (Translated from German)
[13]	A. Grothendieck, "Produits tensoriels topologiques et espaces nucléaires" Mem. Amer. Math. Soc. , 16 (1955) pp. 1–140
[14]	M. Valdivia, "Topics in locally convex spaces" , North-Holland (1982)
[15]	G. Köthe, "Topological vector spaces" , 1–2 , Springer (1969–1979)
[16]	P. Pérez Carrera, J. Bonet, "Barrelled locally convex spaces" , North-Holland (1987)
[17]	A. Fröhlicher, A. Kriegl, "Linear spaces and differentiation theory" , Wiley (1988)
[18]	O.G. Smolyanov, E.T. Shavgulidze, "Continual integrals" , Moscow (1990) (In Russian)

Comments

For (aspects of) infinite-dimensional analysis see e.g. Differential equation, abstract; Qualitative theory of differential equations in Banach spaces; Vector measure; and [a3].

A locally convex topological vector space is quasi-complete if every bounded closed set is complete. Every quasi-complete topological vector space is sequentially complete (every Cauchy sequence has a limit). There are examples of sequentially-complete spaces that are not quasi-complete, and of quasi-complete spaces that are not complete [15]. There is a natural quasi-completion operation, [15], Vol. 1, p. 295.

References

[a1]	J. Horvath, "Topological vector spaces and distributions" , 1 , Addison-Wesley (1968)
[a2]	J. Dugundji, A. Granas, "Fixed point theory" , I , PWN (1982)
[a3]	Yu.L. Daleckii, S.V. Fomin, "Measures and differential equations in infinite-dimensional spaces" , Kluwer (1992) (Translated from Russian)