Tetrahedron, elementary geometry of the
A tetrahedron is a spatial figure formed by four non-co-planar points, called vertices. The term is of Greek origin ( "tetra" meaning "four" and "hedra" meaning "seat" ) and refers to its four plane faces, or sides. As implied in the definition, the usual environment for the study of the tetrahedron is the Euclidean space of three dimensions. Here, it is a convex body (triangular pyramid), the convex hull of its vertices, and, thus, is the natural three-dimensional analogue of the plane triangle, which is determined by three non-collinear points. In fact, as will be shown, the geometry of the triangle constitutes a basis on which much of the geometry of the tetrahedron is built. The first systematic treatment of the tetrahedron was published by J.L. Lagrange in 1773, see [a13].
Whereas the triangle has two sets of proper faces, vertices ( -dimensional faces) and sides (
-dimensional faces) and sides ( -dimensional, or
-dimensional, or 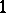 -co-dimensional, faces), the tetrahedron has vertices (
-co-dimensional, faces), the tetrahedron has vertices ( -dimensional faces), edges (
-dimensional faces), edges (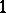 -dimensional, or
-dimensional, or  -co-dimensional, faces, the line segments joining the pairs of vertices), and the triangular sides (
-co-dimensional, faces, the line segments joining the pairs of vertices), and the triangular sides ( -dimensional, or
-dimensional, or 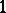 -co-dimensional faces) formed by all
-co-dimensional faces) formed by all  -sets of vertices. If necessary, a face of dimension at least
-sets of vertices. If necessary, a face of dimension at least 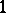 is considered as an (infinite) affine subspace, the affine hull of the original bounded object (cf. also Affine space). Sometimes it is convenient to think in terms of three pairs of opposite edges, joining complementary pairs of vertices and to associate with each vertex the opposite side, formed by the three remaining vertices, and vice versa.
is considered as an (infinite) affine subspace, the affine hull of the original bounded object (cf. also Affine space). Sometimes it is convenient to think in terms of three pairs of opposite edges, joining complementary pairs of vertices and to associate with each vertex the opposite side, formed by the three remaining vertices, and vice versa.
As expected, the vertices are normally labeled  ,
, 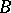 ,
, 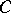 , and
, and 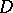 . For the edges (and their lengths) bounding the triangle
. For the edges (and their lengths) bounding the triangle  one may use Euler's notation:
one may use Euler's notation: 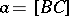 ,
, 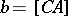 ,
, 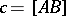 , with the opposite edges indicated by a prime:
, with the opposite edges indicated by a prime: 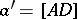 ,
, 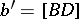 ,
, 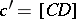 . A subscripting scheme is often more useful when certain analytic arguments are employed. Here, one takes
. A subscripting scheme is often more useful when certain analytic arguments are employed. Here, one takes 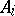 ,
, 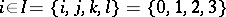 , as labels for the vertices and
, as labels for the vertices and 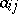 ,
, 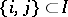 , for the edge (and its length) connecting
, for the edge (and its length) connecting 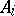 and
and 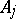 . Thus,
. Thus,  for
for 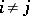 , with the understanding that
, with the understanding that 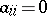 .
.
If the area of the side opposite the vertex 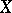 is denoted by
is denoted by 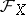 , then the surface area of the tetrahedron is given by
, then the surface area of the tetrahedron is given by
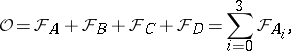 |
while the volume 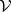 can be computed from the formula
can be computed from the formula
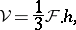 |
where 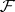 denotes the area of any side and
denotes the area of any side and 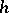 the corresponding height, the distance of the side under consideration from the parallel plane containing the opposite vertex. The volume
the corresponding height, the distance of the side under consideration from the parallel plane containing the opposite vertex. The volume 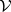 of a tetrahedron is also given by
of a tetrahedron is also given by
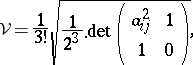 |
which may be regarded as a three-dimensional analogue to Heron's formula for the area of a triangle (cf. also Heron formula), i.e.,
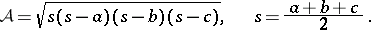 |
Here,
 |
is short for
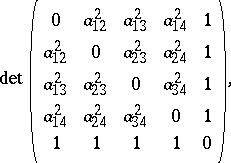 |
the Cayley–Menger determinant of 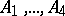 .
.
As a bonus result, the above formula for 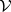 provides a necessary (and also almost sufficient) condition
provides a necessary (and also almost sufficient) condition
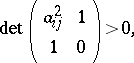 |
for the six numbers 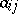 to be the edge lengths of a non-degenerate tetrahedron, an analogue of the famous triangle inequalities (cf. Plane trigonometry). Furthermore, it implies that the three products
to be the edge lengths of a non-degenerate tetrahedron, an analogue of the famous triangle inequalities (cf. Plane trigonometry). Furthermore, it implies that the three products 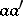 ,
, 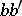 ,
, 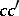 (Euler's notation) satisfy the plane triangle inequalities.
(Euler's notation) satisfy the plane triangle inequalities.
Another spatial analogue of the triangle inequalities is as follows. A set of four positive numbers can represent the areas of the sides of a tetrahedron if and only if the largest is smaller than the sum of the other three, see [a3], [a5]. From this, one may also derive, by means of the first given formula for the volume, a necessary and sufficient condition for four lengths to be the heights of a tetrahedron. But a tetrahedron is (up to congruence) uniquely determined by six pieces, or conditions, and so is not uniquely determined by four suitable areas or four suitable heights.
There are two types of angles connected with a tetrahedron: six dihedral angles (cf. Dihedral angle), formed by all possible pairs of sides, and four trihedral angles, formed by all possible triples of sides. The sum 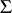 of the dihedral angles varies between
of the dihedral angles varies between 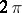 and
and 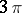 while the sum
while the sum  of the trihedral angles varies between
of the trihedral angles varies between  and
and  ; both sums are related by
; both sums are related by
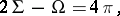 |
see [a1]. The dihedral angles may be acute, right or obtuse, but there must exist at least three acute angles. More precisely, a distribution of acute, right or obtuse angles is possible if and only if the graph formed by one vertex for each side and one edge for each acute dihedral angle between the corresponding sides is connected, see [a3].
The circumcircle and the incircle of the triangle have immediate analogues. Consider the perpendicular bisecting plane of each edge; then for each side the three corresponding planes share a line perpendicular to this side. The six planes and four lines obtained in this way intersect in the circumcentre of the tetrahedron, the centre of the circumsphere with radius
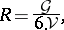 |
where  denotes the area of the triangle with sides
denotes the area of the triangle with sides  ,
, 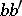 ,
, 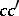 . For the incentre and the insphere, the six angle-bisecting planes of the dihedral angles have a point in common; the inradius is given by
. For the incentre and the insphere, the six angle-bisecting planes of the dihedral angles have a point in common; the inradius is given by
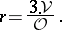 |
However, the treatment of exspheres requires special attention. The natural analogues of the excircles are the exspheres of the first kind, touching one side from the exterior, but there may also be between zero and three exspheres of the second kind, touching two sides from the exterior, see [a9]. There are no exspheres of the second kind if and only if the tetrahedron is isosceles, i.e., all sides have equal area, or, equivalently, opposite edges have equal length. See [a12] for other characterizations of isosceles tetrahedra. There are three exspheres of the second kind if and only if the sum of the areas of two sides is never equal to the sum of the areas of the other two. The radius of the exsphere touching only the side opposite to the vertex 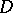 from the outside is given by
from the outside is given by
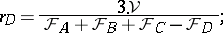 |
the radius of the exsphere touching the sides opposite to the vertices 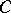 and
and 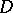 from the outside (if it exists) is given by
from the outside (if it exists) is given by
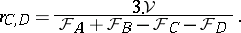 |
A sphere touching all the edges of a tetrahedron (an edge-touching sphere) exists if and only if each of the following conditions is satisfied:
i) 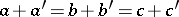 ;
;
ii) the incircles of the sides touch each other;
iii) the perpendiculars to the sides through the incentres concur in the centre of the edge touching sphere.
iv) the vertices are centres of four pairwise touching spheres with radii 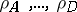 , see [a6]. In particular,
, see [a6]. In particular,
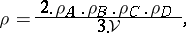 |
where 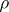 represents the radius of the edge-touching sphere. Furthermore, in any class of tetrahedra with equal heights, there is exactly one tetrahedron with an edge-touching sphere, see [a7].
represents the radius of the edge-touching sphere. Furthermore, in any class of tetrahedra with equal heights, there is exactly one tetrahedron with an edge-touching sphere, see [a7].
In fact, many of the special points, lines and incidence relations associated with the plane triangle do not have unique analogues in the case of the tetrahedron. The following examples should help to substantiate this claim.
a) There are two types of medians for a tetrahedron: the six planes each containing one edge and the middle point of the opposite edge, and the four lines connecting a vertex 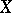 to the centroid
to the centroid 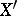 of the opposite side,
of the opposite side, 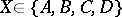 . All these ten geometric objects intersect in one point, the centroid of the tetrahedron, which divides the line segments
. All these ten geometric objects intersect in one point, the centroid of the tetrahedron, which divides the line segments 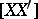 in the ratio
in the ratio 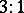 . The central stretching with the centroid as centre and ratio
. The central stretching with the centroid as centre and ratio 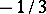 transforms the circumsphere in the Feuerbach sphere of the first kind. The centroid is also the middle point of the three line segments connecting the middle points of opposite edges. These line segments have equal lengths if and only if the tetrahedron is orthocentric, a property discussed below. In this case the centroid is the centre of a sphere intersecting the sides in the respective Feuerbach nine-point circles (cf. Nine-point circle), the Feuerbach sphere of the second kind.
transforms the circumsphere in the Feuerbach sphere of the first kind. The centroid is also the middle point of the three line segments connecting the middle points of opposite edges. These line segments have equal lengths if and only if the tetrahedron is orthocentric, a property discussed below. In this case the centroid is the centre of a sphere intersecting the sides in the respective Feuerbach nine-point circles (cf. Nine-point circle), the Feuerbach sphere of the second kind.
b) In case of the altitudes, G. Monge [a15] took the planes perpendicular to one edge containing the middle point of the opposite edge. The six planes obtained concur in the Monge point, coinciding with the external centre of similitude of the circumsphere and the Feuerbach sphere of the first kind. Thus the centroid is the middle point of the line segment connecting the circumcentre and the point of Monge, see [a15]. On the other hand, the altitudes of a tetrahedron (as lines) are defined as the perpendiculars to the sides passing through the respective opposite vertices, see the definition of height given above. A tetrahedron is called orthocentric if the altitudes concur in a point, the orthocentre of the tetrahedron. The following conditions are equivalent:
i) the tetrahedron is orthocentric;
ii) the three parallelograms 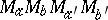 ,
, 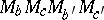 and
and 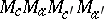 , where
, where  denotes the middle point of the edge
denotes the middle point of the edge  , are rectangles;
, are rectangles;
iii) opposite edges are perpendicular;
iv) 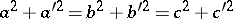 ;
;
v) the line segments 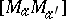 ,
, 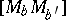 and
and 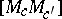 have equal lengths;
have equal lengths;
vi) the feet of the altitudes, the intersection points of the altitudes and the respective sides, are the orthocentres of the sides considered as triangles. In condition ii), it suffices to require that only two of the mentioned parallelograms are rectangles, while condition iii) is fulfilled if and only if two pairs of opposite edges are perpendicular. In condition vi) it suffices to consider just one foot of an altitude, see [a4].
More generally, the following conditions on a tetrahedron 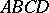 are equivalent:
are equivalent:
i) the altitudes through 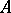 and
and  ,
, 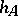 and
and 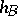 , intersect in a unique point
, intersect in a unique point 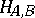 ;
;
ii) the altitudes 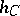 and
and 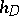 intersect in a unique point
intersect in a unique point 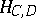 ;
;
iii) the edges 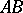 and
and 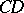 are perpendicular;
are perpendicular;
iv) the parallelogram 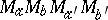 is a rectangle;
is a rectangle;
v) 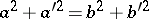 ;
;
vi) the line segments 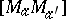 and
and 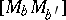 have equal lengths. A tetrahedron with just one pair of perpendicular opposite edges is called semi-orthocentric and can always be labeled in such a way that the given conditions are fulfilled. In this case, the plane formed by the altitudes
have equal lengths. A tetrahedron with just one pair of perpendicular opposite edges is called semi-orthocentric and can always be labeled in such a way that the given conditions are fulfilled. In this case, the plane formed by the altitudes 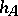 and
and 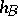 and that formed by the altitudes
and that formed by the altitudes 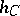 and
and  intersect in the line
intersect in the line 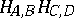 , with the point of Monge being the middle point of the line segment
, with the point of Monge being the middle point of the line segment 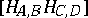 .
.
The altitudes of a tetrahedron with no pair of perpendicular opposite edges are pairwise skew (cf. Skew lines), but belong to a equilateral hyperboloid whose centre is the point of Monge, see [a16]. A geometric description of the axes of this hyperboloid is an open problem (1996).
In case of an orthocentric tetrahedron, the point of Monge coincides with the orthocentre. In addition, an orthocentric tetrahedron has an edge-touching sphere if and only if it is a regular pyramid, i.e., one side is an equilateral triangle and the three edges not contained in this side have equal lengths. In this case one also has the identities
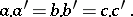 |
Tetrahedra with this property are sometimes called iso-dynamic.
Orthocentric tetrahedra have a lot of extremal properties, see [a10]. An example is the following: Given four concentric spheres 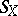 ,
, 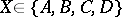 , the tetrahedra with maximal volume among all tetrahedra
, the tetrahedra with maximal volume among all tetrahedra  with
with 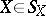 for all
for all  are orthocentric; the common centre of the spheres
are orthocentric; the common centre of the spheres  is the orthocentre of these maximal tetrahedra.
is the orthocentre of these maximal tetrahedra.
An analogue to the Pythagoras theorem holds for tri-rectangular tetrahedra, i.e., tetrahedra such that three concurrent edges are pairwise perpendicular. If these edges concur in the vertex 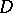 , then
, then
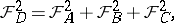 |
see [a2].
In addition, there are analogues to the Gauss and Bodenmiller theorems (cf. Gauss theorem; Bodenmiller theorem) for tetrahedra, see [a8].
An interesting result related to the edge-touching sphere of a tetrahedron is given in [a7], whereby a question raised in elementary particle physics leads from the edge-touching sphere to Steiner's Rome surface which, in the Euclidean  -dimensional space, is given by the equation
-dimensional space, is given by the equation
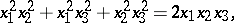 |
intersecting the sides of the regular tetrahedron with vertices  ,
,  ,
, 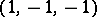 ,
, 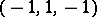 in the respective incircles.
in the respective incircles.
As with the triangle, there are many known inequalities relating various parts of the tetrahedron. For example, the triangle inequality 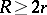 (where
(where 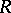 is the circumradius and
is the circumradius and  the inradius), with equality for equilateral triangles, reads for the tetrahedron:
the inradius), with equality for equilateral triangles, reads for the tetrahedron:  , with equality for the regular case. Actually, these are both special cases of the
, with equality for the regular case. Actually, these are both special cases of the  -simplex inequality (in
-simplex inequality (in  -dimensional Euclidean space
-dimensional Euclidean space 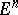 )
)  , with equality for the regular simplex. For these, and other inequalities, see [a14].
, with equality for the regular simplex. For these, and other inequalities, see [a14].
Most of the properties given above have generalizations to higher-dimensional simplices; see the bibliography.
References
| [a1] | T. Egger, R. Fritsch, K. Seebach, "Zum Winkelsummensatz für Tetraeder" Didaktik der Math. , 11 (1983) pp. 14–35 |
| [a2] | J. Faulhaber, "Miracula Arithmetica" , David Franck (1622) |
| [a3] | M. Fiedler, "Geometrie simplexu v 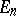 " Časopis Pěst. Mat. , 79 (1954) pp. 297–320 " Časopis Pěst. Mat. , 79 (1954) pp. 297–320 |
| [a4] | R. Fritsch, "Höhenschnittpunkte für  -Simplizes" Elem. Math. , 31 (1995) pp. 1–8 -Simplizes" Elem. Math. , 31 (1995) pp. 1–8 |
| [a5] | R. Fritsch, "Dreiecksungleichungen für Tetraeder" Der mathem. und naturwissenschaftl. Unterr. , 34 (1981) pp. 274–278 |
| [a6] | R. Fritsch, "Kantenkugeln-geometrische Anwendungen der linearen Algebra" Math. Semesterber. , 32 (1985) pp. 84–109 |
| [a7] | R. Fritsch, "Energietetraeder?" Mitteil. Math. Sem. Giessen (Coxeter Festschrift II) , 164 (1984) pp. 151–177 |
| [a8] | R. Fritsch, "An  -dimensional Bodenmiller theorem" Crux Mathematicorum , 21 (1995) pp. 109–113 -dimensional Bodenmiller theorem" Crux Mathematicorum , 21 (1995) pp. 109–113 |
| [a9] | L. Gerber, "Spheres tangent to all the faces of a simplex" J. Combin. Th. , 12 (1972) pp. 453–456 |
| [a10] | L. Gerber, "The orthocentric simplex as an extreme simplex" Pacific J. Math. , 56 (1975) pp. 97–111 |
| [a11] | J.C.H. Gerretsen, "An analogue of the nine-point circle in the space of  dimensions" Indagationes Mathematicae , 7 (1945) pp. 123–124 dimensions" Indagationes Mathematicae , 7 (1945) pp. 123–124 |
| [a12] | Y.S. Kupitz, H. Martini, "The Fermat–Torricelli point and isosceles tetrahedra" J. Geom. , 49 (1994) pp. 150–162 |
| [a13] | J.L. Lagrange, "Solutions analytiques de quelques problèmes sur le pyramides triangulaires" Nouveaux Mem. Acad. R. des Sci. et Belles-Lettres (1773) pp. 149–176 |
| [a14] | D.S. Mitrinović, J.E. Pečaric, V. Volenec, "Recent advances in geometric inequalities" , Kluwer Acad. Publ. (1989) |
| [a15] | G. Monge, "Sur la pyramide triangulaire" Corresp. Ecole Imp. Polytechnique , 2/3 (1811) pp. 263–266 |
| [a16] | J. Steiner, "Aufgaben und Lehrsätze" J. Reine Angew. Math. , 2 (1827) pp. 96–98 |
Tetrahedron, elementary geometry of the. R. EddyR. Fritsch (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tetrahedron,_elementary_geometry_of_the&oldid=17970