Statistical hypotheses, verification of
statistical hypotheses testing
One of the basic parts of mathematical statistics, expounding ideas and methods for the statistical testing of correspondences between experimental data on the one hand and hypotheses on their probability characteristics on the other.
Let a random vector $ X = ( X _ {1} \dots X _ {n} ) $ be observed, taking values $ x = ( x _ {1} \dots x _ {n} ) $ in a measurable space $ ( \mathfrak X _ {n} , {\mathcal B} _ {n} ) $, and suppose it is known that the probability distribution of $ X $ belongs to a given set of probability distributions $ H = \{ { {\mathsf P} _ \theta } : {\theta \in \Theta } \} $, where $ \Theta $ is a certain parametric set. $ H $ is called the set of admissible hypotheses, and any non-empty subset $ H _ {i} $ of it is called a statistical hypothesis, or simply a hypothesis. If $ H _ {i} $ contains precisely one element, then the hypothesis is said to be simple, otherwise it is said to be compound. Moreover, if there are two so-called competing hypotheses distinguished in $ H $:
$$ H _ {0} = \{ { {\mathsf P} _ \theta } : {\theta \in \Theta _ {0} \subset \Theta } \} $$
and
$$ H _ {1} = H \setminus H _ {0} = \ \{ { {\mathsf P} _ \theta } : {\theta \in \Theta _ {1} = \Theta \setminus \Theta _ {0} } \} , $$
then one of which, for example $ H _ {0} $, is called the null, and the other the alternative, hypothesis. In terms of $ H _ {0} $ and $ H _ {1} $, the basic problem in the theory of statistical hypotheses testing can be conveniently formulated using the Neyman–Pearson model (see , [2]). Namely, find an optimal method that makes it possible, on the basis of an observed realization of $ X $, to test whether the hypothesis $ H _ {0} $: $ \theta \in \Theta _ {0} $ is correct, according to which the probability distribution of $ X $ belongs to the set $ H _ {0} = \{ { {\mathsf P} _ \theta } : {\theta \in \Theta _ {0} } \} $, or whether the alternative hypothesis $ H _ {1} $: $ \theta \in \Theta _ {1} $ is correct, according to which the probability distribution of $ X $ belongs to the set
$$ H _ {1} = \{ { {\mathsf P} _ \theta } : {\theta \in \Theta _ {1} = \Theta \setminus \Theta _ {0} } \} . $$
Example 1.
Let a random vector $ X = ( X _ {1} \dots X _ {n} ) $ be observed, with components $ X _ {1} \dots X _ {n} $ that are independent identically-distributed random variables subject to the normal law $ N _ {1} ( \theta , 1) $, with unknown mathematical expectation $ \theta = {\mathsf E} X _ {i} $ $ ( | \theta | < \infty ) $, while the variance is equal to 1, i.e. for any real number $ x $,
$$ {\mathsf P} \{ X _ {i} < x \mid \theta \} = \ \Phi ( x- \theta ) = \ \frac{1}{\sqrt {2 \pi } } \int\limits _ {- \infty } ^ { x } e ^ {-( t- \theta ) ^ {2} /2 } dt, $$
$$ i = 1 \dots n. $$
Under these conditions it is possible to examine the problem of testing $ H _ {0} $: $ \theta = \theta _ {0} $ against $ H _ {1} $: $ \theta \neq \theta _ {0} $, where $ \theta _ {0} $ is a given number. In the given example, $ H _ {0} $ is a simple, while $ H _ {1} $ is a compound hypothesis.
Formally, the competing hypotheses $ H _ {0} $ and $ H _ {1} $ are equivalent in the problem of choosing between them, and the question of which of these two non-intersecting and mutually-complementary sets from $ H $ should be called the null hypothesis is not vital, and does not affect the construction of the theory of statistical hypotheses testing itself. However, as a rule, the researcher's attitude to the problem itself affects the choice of the null hypothesis, with the result that the null hypothesis is often taken to be that subset $ H _ {0} $ of the set $ H $ of all admissible hypotheses that in the researcher's opinion, bearing in mind the nature of the phenomenon in question, or in the light of any physical considerations, will best fit in with the expected experimental data. For this very reason, $ H _ {0} $ is often called the hypothesis to be tested. On a theoretical plan, the difference between $ H _ {0} $ and $ H _ {1} $ is often explained by the fact that, as a rule, $ H _ {0} $ has a simpler structure than $ H _ {1} $, as reflected in the researcher's preference for the simpler model.
In the theory of statistical hypotheses testing, the decision on the correctness of $ H _ {0} $ or $ H _ {1} $ is taken on the basis of an observed realization of the random vector $ X $; the decision principle used in taking the decision "the hypothesis Hi is correct" $ ( i = 0, 1) $, is called a statistical test. The structure of any statistical test is completely defined by its so-called critical function $ \phi _ {n} ( \cdot ) : \mathfrak X _ {n} \rightarrow [ 0, 1] $. According to the statistical test with critical function $ \phi _ {n} ( \cdot ) $, the hypothesis $ H _ {0} $ to be tested is rejected with probability $ \phi _ {n} ( X) $ in favour of the alternative $ H _ {1} $, while $ H _ {1} $ is rejected with probability $ 1- \phi _ {n} ( X) $ in favour of $ H _ {0} $. From a practical point of view, the most interesting are the so-called non-randomized tests, whose critical functions take only two values: 0 and 1. Whichever the test used in choosing between $ H _ {0} $ and $ H _ {1} $, it may lead either to a correct or a false decision being taken. In the theory of statistical hypotheses testing, wrong inferences are classified in the following way.
If the test rejects the hypothesis $ H _ {0} $ to be tested when in reality it is correct, then one says that an error of the first kind has been committed. Conversely, if the test does not reject $ H _ {0} $( and, in this test, $ H _ {0} $ is therefore accepted) when it is in fact incorrect, then one says that an error of the second kind has been committed. The problem of testing $ H _ {0} $ against $ H _ {1} $ should ideally be approached in such a way as to minimize the probabilities of these errors. Unfortunately, it is impossible, given the fixed dimension $ n $ of the vector of observations of $ X $, to control both error probabilities simultaneously: as a rule, as one decreases, so the other increases. The probabilities of these errors are expressed numerically in terms of the so-called power function $ \beta _ {n} ( \cdot ) $ of the statistical test, defined on the set $ \Theta = \Theta _ {0} \cup \Theta _ {1} $ by means of the rule:
$$ \beta _ {n} ( \theta ) = \ {\mathsf E} _ \theta \phi _ {n} ( X) = \ \int\limits _ { \mathfrak X } \phi _ {n} ( x) d {\mathsf P} _ \theta ( x),\ \ \theta \in \Theta = \Theta _ {0} \cup \Theta _ {1} . $$
It follows from the definition of the power function $ \beta _ {n} ( \cdot ) $ that if the random vector $ X $ is subject to the law $ {\mathsf P} _ \theta $, $ \theta \in \Theta = \Theta _ {0} \cup \Theta _ {1} $, then the statistical test based on the critical function $ \phi _ {n} ( \cdot ) $ will reject the hypothesis $ H _ {0} $ to be tested with probability $ \beta _ {n} ( \Theta ) $. Thus, the restriction of the power function $ \beta _ {n} ( \cdot ) $ from $ \Theta $ to $ \Theta _ {0} $ will show the probability of errors of the first kind, i.e. the probability of wrongly rejecting $ H _ {0} $. Conversely, the restriction of $ \beta _ {n} ( \cdot ) $ from $ \Theta $ to $ \Theta _ {1} $, called the power of the statistical test, shows another important quantity of the statistical test: the probability of rejecting the hypothesis $ H _ {0} $ to be tested when in reality the competing hypothesis $ H _ {1} $ is correct. The power of the statistical test is sometimes defined as the number
$$ \beta = \inf _ {\theta \in \Theta _ {1} } \beta _ {n} ( \theta ) = \ \inf _ {\theta \in \Theta _ {1} } {\mathsf E} _ \theta \phi _ {n} ( X). $$
By complementation, i.e. by use of the function $ 1- \beta _ {n} ( \cdot ) $, defined on the set $ \Theta _ {1} $, the probability of an error of the second kind can be calculated.
The problem of testing $ H _ {0} $ against $ H _ {1} $ using the classical Neyman–Pearson model begins with the choice of an upper bound $ \alpha $ $ ( 0 < \alpha < 1 ) $ for the probability of wrongly rejecting $ H _ {0} $, i.e. for the probability of an error of the first kind, and, given this bound $ \alpha $, the test with the greatest power is then sought. Owing to the special role played by $ H _ {0} $ in the researcher's work, the number $ \alpha $, called the significance level of the test, is taken to be sufficiently small, equal for example to 0.01; 0.05; 0.1; etc. The choice of the significance level $ \alpha $ means that the set of all statistical tests designed to test $ H _ {0} $ against $ H _ {1} $ is restricted to the set of those tests satisfying the condition
$$ \tag{1 } \sup _ {\theta \in \Theta _ {0} } \beta _ {n} ( \theta ) = \ \sup _ {\theta \in \Theta _ {0} } {\mathsf E} _ \theta \phi _ {n} ( X) = \ \alpha . $$
(It is sometimes required that, instead of condition (1), $ \sup _ {\theta \in \Theta _ {0} } \beta _ {n} ( \theta ) \leq \alpha $, which makes no difference to the general theory of statistical hypotheses testing.) A statistical test that satisfies (1) is called a test at level $ \alpha $. Thus, in the classical formulation, the problem of testing $ H _ {0} $ against $ H _ {1} $ reduces to the construction of a statistical test at level $ \alpha $ whose power function satisfies the condition
$$ \tag{2 } \beta _ {n} ^ \star ( \theta ) \geq \beta _ {n} ( \theta ) \ \ \textrm{ for } \textrm{ all } \theta \in \Theta _ {1} , $$
where $ \beta _ {n} ( \cdot ) $ is the power function of an arbitrary test at level $ \alpha $. If $ H _ {0} $ and $ H _ {1} $ are simple, an effective solution of this optimization problem is provided by the likelihood-ratio test. If $ H _ {1} $ is compound, however, then it is rare for a statistical test to satisfy condition (2). However, if such a test does exist, then it is recognized as the best test of $ H _ {0} $ against $ H _ {1} $, and is called the uniformly most-powerful test at level $ \alpha $ in the problem of choosing between $ H _ {0} $ and $ H _ {1} $. Since uniformly most-powerful tests exist only rarely, the class of statistical tests has to be restricted by means of certain extra requirements, such as unbiasedness, similarity, completeness, and others, and the best test in the sense of (2) has to be constructed in this narrower class. For example, the requirement that the test be unbiased means that its power function must satisfy the relation
$$ \sup _ {\theta \in \Theta _ {0} } \beta _ {n} ( \theta ) \leq \inf _ { \theta \in \Theta _ {1} } \beta _ {n} ( \theta ). $$
Example 2.
Under the conditions of example 1, for any fixed significance level $ \alpha $, a non-randomized, uniformly most-powerful, unbiased test of level $ \alpha $ exists for testing $ H _ {0} $ against $ H _ {1} $, namely the likelihood-ratio test. The critical function of this best test is defined as:
$$ \phi _ {n} ( X) = \left \{ \begin{array}{ll} 1 & \textrm{ if } | \overline{X}\; - \theta _ {0} | > \frac{1}{\sqrt n } \Phi ^ {-} 1 \left ( 1- \frac \alpha {2} \right ) , \\ 0 & \textrm{ if } | \overline{X}\; - \theta _ {0} | \leq \frac{1}{\sqrt n } \Phi ^ {-} 1 \left ( 1- \frac \alpha {2} \right ) , \\ \end{array} \right . $$
where
$$ \overline{X}\; = \frac{X _ {1} + \dots + X _ {n} }{n} . $$
Owing to the fact that the statistic $ \overline{X}\; $, called the test statistic, is subject to the normal law $ N _ {1} ( \theta , 1/n) $ with parameters $ {\mathsf E} \overline{X}\; = \theta $ and $ {\mathsf D} \overline{X}\; = 1/n $, i.e. for any real number $ x $,
$$ {\mathsf P} \{ \overline{X}\; < x \mid \theta \} = \Phi [ \sqrt n ( x- \theta )], $$
the power function $ \beta _ {n} ( \cdot ) $ of the best test for testing $ H _ {0} $ against $ H _ {1} $ is expressed by the formula
$$ \beta _ {n} ( \theta ) = {\mathsf E} _ \theta \phi _ {n} ( X) = $$
$$ = \ {\mathsf P} \left \{ | \overline{X}\; - \theta _ {0} | > \frac{1}{\sqrt n } \Phi ^ {-} 1 \left ( 1- \frac \alpha {2} \right ) \mid \Theta \right \} = $$
$$ = \ \Phi \left [ \Phi ^ {-} 1 \left ( \frac \alpha {2} \right ) + \sqrt n ( \theta _ {0} - \theta ) \right ] + \Phi \left [ \Phi ^ {-} 1 \left ( \frac \alpha {2} \right ) - \sqrt n ( \theta _ {0} - \theta ) \right ] , $$
where $ \beta _ {n} ( \theta ) \geq \beta _ {n} ( \theta _ {0} ) = \alpha $. The figure below gives a graphical representation of the behaviour of the power function $ \beta _ {n} ( \cdot ) $.
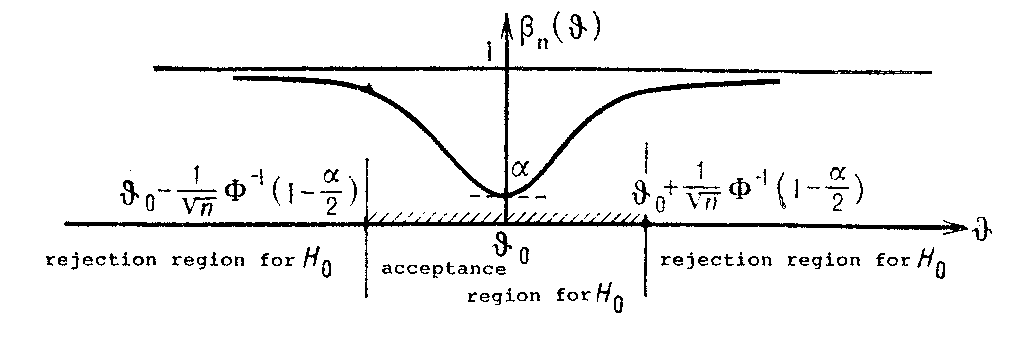
Figure: s087400a
The function $ \beta _ {n} ( \cdot ) $ attains its lowest value, equal to the significance level $ \alpha $, at the point $ \theta = \theta _ {0} $, and by moving $ \theta $ away from $ \theta _ {0} $, its values increase, getting nearer to 1 as $ | \theta - \theta _ {0} | $ increases.
The theory of statistical hypotheses testing enables one to treat the different problems that arise in practice from the same point of view: the construction of interval estimators for unknown parameters, the estimation of the divergence between mean values of probability laws, the testing of hypotheses on the independence of observations, problems of statistical quality control, etc. Thus, in example 2, the acceptance region of $ H _ {0} $ is the best confidence interval with confidence coefficient $ 1 - \alpha $ for the unknown mathematical expectation $ \theta $.
Apart from the classical Neyman–Pearson approach, there are other methods for solving the problem of choosing between hypotheses: the Bayesian approach, the minimax approach, the Wald method of sequential testing, and others. Moreover, the theory of statistical hypotheses testing also includes approximate methods based on the study of the asymptotic behaviour of a sequence $ \{ \beta _ {n} ( \cdot ) \} $ of power functions of statistical tests of $ H _ {0} $ against $ H _ {1} $, when the dimension $ n $ of the vector of observations of $ X = ( X _ {1} \dots X _ {n} ) $ increases unboundedly. In this situation it is usually required that the constructed sequence of tests be consistent, i.e. that
$$ \lim\limits _ {n \rightarrow \infty } \beta _ {n} ( \theta ) = 1 \ \ \textrm{ for } \textrm{ any } \theta \in \Theta _ {1} , $$
which means that as $ n $ increases, the hypotheses $ H _ {0} $ and $ H _ {1} $ can be distinguished with a greater degree of certainty. In example 2, a consistent sequence of tests is constructed (if $ n \rightarrow \infty $).
In any case, whatever the statistical test used, the acceptance of either hypothesis does not mean that it is necessarily the correct one, but simply that there is no evidence at this stage to contradict it. Precisely because of this agreement between theory and experience, the researcher has no reason not to believe that his choice is correct until such time as new observations appear that might force him to change his attitude towards the chosen hypothesis, and perhaps even towards the whole model.
References
| [1a] | J. Neyman, E.S. Pearson, "On the use and interpretation of certain test criteria for purposes of statistical inference I" Biometrika , 20A (1928) pp. 175–240 |
| [1b] | J. Neyman, E.S. Pearson, "On the use and interpretation of certain test criteria for purposes of statistical inference II" Biometrika , 20A (1928) pp. 263–294 |
| [2] | J. Neyman, E.S. Pearson, "On the problem of the most efficient tests of statistical hypotheses" Phil. Trans. Roy. Soc. London Ser. A , 231 (1933) pp. 289–337 |
| [3] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1988) |
| [4] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) |
| [5] | J. Hájek, Z. Sidák, "Theory of rank tests" , Acad. Press (1967) |
| [6] | M.S. Nikulin, "A result of Bol'shev's from the theory of the statistical testing of hypotheses" J. Soviet Math. , 44 : 3 (1989) pp. 522–529 Zap. Nauchn. Sem. Mat. Inst. Steklov. , 153 (1986) pp. 129–137 |
Statistical hypotheses, verification of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Statistical_hypotheses,_verification_of&oldid=49601