Spherical geometry
An area of mathematics concerned with geometric figures on a sphere, in the same way as planimetry is concerned with geometric figures in a plane.
Every plane that intersects a sphere gives a certain circle as section; if the intersecting plane passes through the centre $O$ of the sphere, then a so-called great circle is obtained as the intersection. A unique great circle can be drawn through any two points $A$ and $B$ on the sphere (Fig. a), except when they are diametrically opposite.
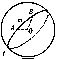
Figure: s086680a
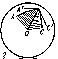
Figure: s086680b
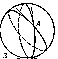
Figure: s086680c
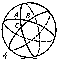
Figure: s086680d
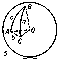
Figure: s086680e
Figure: s086680f
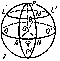
Figure: s086680g

Figure: s086680h
The great circles of a sphere are its geodesics (cf. Geodesic line), and for this reason their role in spherical geometry is the same as the role of straight lines in planimetry. However, whereas any segment of a straight line is the shortest curve between its ends, an arc of a great circle on a sphere is only the shortest curve when it is shorter than the complementary arc. Spherical geometry differs from planimetry in many other senses; for example, there are no parallel geodesic lines: two great circles always intersect, and, moreover, they intersect in two points.
The length of a segment $AB$ on a sphere, i.e. the length of the arc $AmB$ (Fig. a) of a great circle, is measured by its corresponding central angle $AOB$. The angle $ABC$ (Fig. b) formed on the sphere by the arcs of two great circles is measured by the angle $A'BC'$ between the tangents of the corresponding arcs at the point of intersection $B$ or by the dihedral angle formed by the planes $OBA$ and $OBC$.
When two great circles intersect on a sphere, four spherical digons, or lunes, are formed (Fig. c). A lune is defined by specifying its angle. The area of a lune is determined by the formula $S=2R^2A$, where $R$ is the radius of the sphere and $A$ is the angle of the lune expressed in radians.
Three great circles that do not intersect in one pair of diametrically-opposite points form eight spherical triangles on the sphere (Fig. d); if the elements (angles and sides) of one of these is known, it is easy to determine the elements of all the others. It is therefore usual to consider only triangles whose sides and angles are less than $\pi$ (such triangles are called Euler triangles). The sides $a,b,c$ of a spherical triangle are measured by the planar angles of the trihedral angle $OABC$ (Fig. e); the angles $A,B,C$ of the triangle are measured by the dihedral angles of that same trihedral angle. The properties of spherical triangles vary greatly from the properties of triangles on a plane (rectilinear triangles). Thus, a fourth case of equality for triangles on a sphere can be added to the three already known for rectilinear triangles: Two triangles are equal if their corresponding angles are equal (on a sphere, similar triangles do not exist).
Triangles that can be matched up by a movement around the sphere are said to be directly congruent. Such triangles have equal elements and the same orientation. Triangles that have equal elements and a different orientation are called oppositely symmetric; the triangles $AC'C$ and $BCC'$ in Fig. fform an example.
In every spherical (Euler) triangle, each side is less than the sum of, and more than the difference between, the other two; the sum of all the sides is always less than $2\pi$. The sum of the angles of a spherical triangle is always less than $3\pi$ and more than $\pi$. The difference $s-\pi=\epsilon$, where $s$ is the sum of the angles of a spherical triangle, is called the spherical excess. The area of a spherical triangle is defined by the formula $S=R^2\epsilon$, where $R$ is the radius of the sphere. For the relationship between the angles and sides of a spherical triangle, see Spherical trigonometry.
The position of each point on a sphere is completely defined by the specification of two numbers; these two numbers (coordinates) can be defined in the following way (Fig. g). A great circle $QQ'$ (the equator) is fixed, along with one of the two points of intersection of the diameter $PP'$ of the sphere perpendicular to the plane of the equator and the surface of the sphere, for example $P$ (the pole), as well as one of the great semi-circles $PAP'$ that emanate from the pole (the zero meridian). The great semi-circles of the sphere that emanate from $P$ are called meridians, while its small circles, which are parallel to the equator, are called parallels. One of the coordinates of the point $M$ on the sphere is the angle $\theta=POM$ — the polar distance — while the other is the angle $\phi=AON$ between the zero meridian and the meridian which passes through the point $M$ — the longitude, which is counted anti-clockwise.
The length $L$ of an arc $M_1M_2$ (Fig. h) of the curve $\theta=f(t)$, $\phi=g(t)$ is calculated according to the formula
$$L=\int\limits_{t_1}^{t_2}\sqrt{\left(\frac{df}{dt}\right)^2+\sin f\left(\frac{dg}{dt}\right)^2}dt.$$
References
| [1] | N.N. Stepanov, "Spherical trigonometry" , Leningrad-Moscow (1948) (In Russian) |
| [2] | P.S. Alexandroff [P.S. Aleksandrov] (ed.) et al. (ed.) , Enzyklopaedie der Elementarmathematik , 4. Geometrie , Deutsch. Verlag Wissenschaft. (1969) (Translated from Russian) |
Comments
Let $S=S^d\subset\mathbf R^{d+1}$ be the unit sphere. The points of $S$, i.e. unit length vectors, can be identified with half-lines emanating from the origin in $\mathbf R^{d+1}$. A notion of distance, a metric, on $S$ is defined by $d(x,y)=\arccos(x,y)$, where $(x,y)$ is the inner product of the unit length vectors $x,y$. Let $xy$ and $xz$ be two arcs of great circles in $S$ intersecting, as the notation implies, in $x$. Let $x_y$ be the unit length tangent vector to $xy$ at $x$ and let $x_z$ be analogously defined. Then the angle between $xy$ and $xz$ at $x$ is $\arccos(x_y,x_z)$, which is also the angle between the planes through $O$ cutting out $xy$ and $xz$.
As mentioned above, a spherical triangle with sides $a,b,c$ always satisfies $|b-c|<a<b+c$ and $a+b+c<2\pi$; conversely, if $a,b,c\in(0,\pi)$ and these inequalities are satisfied, then there exists a spherical triangle with these sides.
A pole of a great circle is a point of the sphere perpendicular to the plane cutting out that great circle; i.e. if the great circle is regarded as the equator, the two poles are the North and South Poles.
References
| [a1] | M. Berger, "Geometry" , II , Springer (1987) |
| [a2] | D. Hilbert, S.E. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1952) (Translated from German) |
| [a3] | B.A. [B.A. Rozenfel'd] Rosenfel'd, "A history of non-euclidean geometry" , Springer (1988) (Translated from Russian) |
| [a4] | J.L. Coolidge, "A treatise on the circle and the sphere" , Clarendon Press (1916) |
| [a5] | H.S.M. Coxeter, "Introduction to geometry" , Wiley (1961) pp. 11; 258 |
Spherical geometry. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spherical_geometry&oldid=31870