Representation of the symmetric groups
A linear representation of the group $ S _ {m} $
over a field $ K $.
If $ \mathop{\rm char} K = 0 $,
then all finite-dimensional representations of the symmetric groups are completely reducible (cf. Reducible representation) and defined over $ \mathbf Q $ (in other words, irreducible finite-dimensional representations over $ \mathbf Q $
are absolutely irreducible).
The irreducible finite-dimensional representations of $ S _ {m} $ over $ \mathbf Q $ are classified as follows. Let $ d $ be a Young diagram corresponding to a partition $ \lambda = ( \lambda _ {1} \dots \lambda _ {r} ) $ of the number $ m $, let $ R _ {d} $ (respectively, $ C _ {d} $) be the subgroup of $ S _ {m} $ consisting of all permutations mapping each of the numbers $ 1 \dots m $ into a number in the same row (respectively, column) of $ d $. Then
$$ R _ {d} \simeq \ S _ {\lambda _ {1} } \times \dots \times S _ {\lambda _ {r} } $$
and
$$ C _ {d} \simeq \ S _ {\lambda _ {1} ^ \prime } \times \dots \times S _ {\lambda _ {s} ^ \prime } , $$
where $ \lambda ^ \prime = ( \lambda _ {1} ^ \prime \dots \lambda _ {s} ^ \prime ) $ is the partition of $ m $ dual to $ \lambda $. There exists a unique irreducible representation $ T _ \lambda : S _ {m} \rightarrow \mathop{\rm GL} ( U _ \lambda ) $ of $ S _ {m} $ (depending on $ \lambda $ only) with the following properties: 1) in the space $ U _ \lambda $ there is a non-zero vector $ u _ {d} $ such that $ T _ \lambda ( g) u _ {d} = u _ {d} $ for any $ g \in R _ {d} $; and 2) in $ U _ \lambda $ there exists a non-zero vector $ u _ {d} ^ \prime $ such that $ T _ \lambda ( g) u _ {d} ^ \prime = \epsilon ( g) u _ {d} ^ \prime $ for any $ g \in C _ {d} $, where $ \epsilon ( g) = \pm 1 $ is the parity (sign) of $ g $. Representations corresponding to distinct partitions are not equivalent, and they exhaust all irreducible representations of $ S _ {m} $ over $ Q $.
The vectors $ u _ {d} $ and $ u _ {d} ^ \prime $ are defined uniquely up to multiplication by a scalar. For all diagrams corresponding to a partition $ \lambda $ these vectors are normalized such that $ gu _ {d} = u _ {gd} $ and $ gu _ {d} ^ \prime = u _ {gd} ^ \prime $ for any $ g \in S _ {m} $. Here $ gd $ denotes the diagram obtained from $ d $ by applying to all numbers the permutation $ g $. The vectors $ u _ {d} $ (respectively, $ u _ {d} ^ \prime $) corresponding to standard diagrams $ d $ form a basis for $ U _ \lambda $. In this basis the operators of the representation $ T _ \lambda $ have the form of integral matrices. The dimension of $ T _ \lambda $ is
$$ \mathop{\rm dim} T _ \lambda = \ \frac{m! \prod _ {i < j } ( l _ {i} - l _ {j} ) }{\prod _ {i} l _ {i} ! } = \ \frac{m! }{\prod _ {( i, j) } \lambda _ {ij} } , $$
where $ l _ {i} = \lambda _ {i} + r - i $, $ i = 1 \dots r $, and the product in the denominator of the last expression is taken over all cells $ c _ {ij} $ of the Young tableau $ t _ \lambda $; $ \lambda _ {ij} $ denotes the length of the corresponding hook.
To the partition $ ( m) $ corresponds the trivial one-dimensional representation of $ S _ {m} $, while to the partition $ ( 1, \dots, 1) $ corresponds the non-trivial one-dimensional representation $ \epsilon $ (the signature homomorphism, giving the parity or sign representation). To the partition $ \lambda ^ \prime $ dual to $ \lambda $ corresponds the representation $ \epsilon T _ \lambda $. The space $ U _ {\lambda ^ \prime } $ can be identified (in a canonical way, up to a homothety) with $ U _ \lambda $, so that $ T _ {\lambda ^ \prime } ( g) = \epsilon ( g) T _ \lambda ( g) $ for any $ g \in S _ {m} $. Moreover, one may take $ u _ {d} ^ \prime = u _ {d ^ \prime } $, where $ d ^ \prime $ is the diagram obtained from $ d $ by transposition.
The construction of a complete system of irreducible representations of a symmetric group invokes the use of the Young symmetrizer, and allows one to obtain the decomposition of the regular representation. If $ d $ is the Young diagram corresponding to a partition $ \lambda $, then the representation $ T _ \lambda $ is equivalent to the representation of $ S _ {m} $ in the left ideal of the group algebra $ \mathbf Q S _ {m} $ generated by the Young symmetrizer $ e _ {d} $. An a posteriori description of $ e _ {d} $ is the following: $ T _ \mu ( e _ {d} ) = 0 $ for $ \lambda \neq \mu $, and $ T _ \lambda ( e _ {d} ) $ is the operator, of rank 1, acting by the formula $ T _ \lambda ( e _ {d} ) u = ( u _ {d} , u ) u _ {d} ^ \prime $ for any $ u \in U _ \lambda $. Here $ ( , ) $ denotes the invariant scalar product in $ U _ \lambda $, normalized in a suitable manner. Moreover,
$$ ( u _ {d} , u _ {d} ^ \prime ) = \ \frac{m! }{ \mathop{\rm dim} U _ \lambda } . $$
The Frobenius formula gives a generating function for the characters of $ T _ \lambda $. However, recurrence relations are more convenient to use when computing individual values of characters. The Murnagan–Nakayama rule is most effective: Let $ a _ {\lambda \mu } = a _ {\lambda \mu } ^ {(m)} $ be the value of a character of $ T _ \lambda $ on the class $ [ \mu ] $ of conjugate elements of $ S _ {m} $ defined by a partition $ \mu $ of $ m $, and suppose that $ \mu $ contains a number $ p $. Denote by $ \overline \mu $ the partition of $ m - p $ obtained from $ \mu $ by deleting $ p $. Then
$$ a _ {\lambda \mu } ^ {(m)} = \ \sum _ {\overline \lambda } (- 1) ^ {i ( \overline \lambda ) } a _ {\overline \lambda \overline \mu } ^ {( m - p) } , $$
where the sum is over all partitions $ \overline \lambda $ of $ m - p $ obtained by deleting a skew hook of length $ p $ from the Young tableau $ t _ \lambda $, and where $ i ( \overline \lambda ) $ denotes the height of the skew hook taken out.
There is also a method (cf. [5]) by which one can find the entire table of characters of $ S _ {m} $, i.e. the matrix $ A = \| a _ {\lambda \mu } \| $. Let $ M _ \lambda $ be the representation of $ S _ {m} $ induced by the trivial one-dimensional representation of the subgroup $ R _ \lambda = R _ {d} $, where $ d $ is the Young diagram corresponding to the partition $ \lambda $. Let $ M _ \lambda = \sum _ \mu m _ {\lambda \mu } T _ \mu $ and $ M = \| m _ {\lambda \mu } \| $. If one assumes that the rows and columns of $ M $ are positioned in order of lexicographically decreasing indices (partitions), then $ M $ is a lower-triangular matrix with 1's on the diagonal. The value of a character of $ M _ \lambda $ on a class $ [ \mu ] $ is equal to
$$ b _ {\lambda \mu } = \ \frac{c _ \mu | R _ \lambda \cap [ \mu ] | }{| R _ \lambda | } , $$
where $ c _ \mu $ is the order of the centralizer of the permutations (a representative) from $ [ \mu ] $. The matrix $ B = \| b _ {\lambda \mu } \| $ is upper triangular, and one has $ MM ^ {T} = BC ^ {-1} B ^ {T} $, where $ C = \mathop{\rm diag} ( c _ \mu ) $, from which $ M $ can be uniquely found. Then the matrix $ A $ is determined by
$$ A = M ^ {-1} B. $$
The restriction of a representation $ T _ \lambda $ of $ S _ {m} $ to the subgroup $ S _ {m - 1 } $ can be found by the ramification rule
$$ T _ \lambda \mid _ {S _ {m - 1 } } = \ \sum _ { i } T _ {( \lambda _ {1} \dots \lambda _ {i} - 1 \dots \lambda _ {r} ) } , $$
where the summation extends over all $ i $ for which $ \lambda _ {i} > \lambda _ {i + 1 } $ (including $ r $). The restriction of $ T _ \lambda $ to the subgroup $ A _ {m} $ is absolutely irreducible for $ \lambda \neq \lambda ^ \prime $ and splits for $ \lambda = \lambda ^ \prime $ over a quadratic extension of $ \mathbf Q $ into a sum of two non-equivalent absolutely-irreducible representations of equal dimension. The representations of $ A _ {m} $ thus obtained exhaust all its irreducible representations over $ \mathbf C $.
For representations of the symmetric groups in tensors see Representation of the classical groups.
The theory of modular representations of the symmetric groups has also been developed (see, e.g. [5]).
References
| [1] | H. Weyl, "The classical groups, their invariants and representations" , Princeton Univ. Press (1946) MR0000255 Zbl 1024.20502 |
| [2] | F.D. Murnagan, "The theory of group representations" , Johns Hopkins Univ. Press (1938) |
| [3] | M. Hamermesh, "Group theory and its application to physical problems" , Addison-Wesley (1962) MR0136667 Zbl 0100.36704 |
| [4] | C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962) MR0144979 Zbl 0131.25601 |
| [5] | G.D. James, "The representation theory of the symmetric groups" , Springer (1978) MR0513828 Zbl 0393.20009 |
Comments
Let $ R ( S _ {m} ) $ be the free Abelian group generated by the complex irreducible representations of the symmetric group on $ m $ letters, $ S _ {m} $. Now consider the direct sum
$$ R = \oplus _ { m= 0} ^ \infty R( S _ {m} ) ,\ \ R ( S _ {0} ) = \mathbf Z . $$
It is possible to define a Hopf algebra structure on $ R $, as follows. First the multiplication. Let $ \rho $ and $ \tau $ be, respectively, representations of $ S _ {n} $ and $ S _ {m} $. Taking the tensor product defines a representation $ ( g, h) \mapsto \rho ( g) \otimes \sigma ( h) $ of $ S _ {n} \times S _ {m} $. Consider $ S _ {n} \times S _ {m} $ as a subgroup of $ S _ {n+m} $ in the natural way. The product of $ \rho $ and $ \tau $ in $ R $ is now defined by taking the induced representation to $ S _ {n+m} $:
$$ \rho \sigma = \mathrm{Ind} _ {S _ {n} \times S _ {m} } ^ {S _ {n+m} } ( \rho \otimes \sigma ) . $$
For the comultiplication restriction is used. Let $ \rho $ be a representation of $ S _ {n} $. For every $ p, q \in \{ 0, 1 , \dots \} $, $ p+ q = n $, consider the restriction of $ \rho $ to $ S _ {p} \times S _ {q} $ to obtain an element of $ R ( S _ {p} \times S _ {q} ) = R ( S _ {p} ) \otimes R( S _ {q} ) $. The comultiplication of $ R $ is now defined by
$$ \mu = \sum _ { p+ q= n} \mathrm{Res} _ {S _ {p} \times S _ {q} } ^ {S _ {n} } ( \rho ) . $$
There is a unit mapping $ e : \mathbf Z \rightarrow R $, defined by identifying $ \mathbf Z $ and $ R( S _ {0} ) $, and an augmentation $ \epsilon : R \rightarrow \mathbf Z $, defined by $ \epsilon = $ identity on $ R( S _ {0} ) = \mathbf Z $ and $ \epsilon ( R( S _ {m} )) = 0 $ if $ m > 0 $. It is a theorem that $ ( m, \mu , e , \epsilon ) $ define a graded bi-algebra structure on $ R $. There is also an antipode, making $ R $ a graded Hopf algebra.
This Hopf algebra can be explicitly described as follows. Consider the commutative ring of polynomials in infinitely many variables $ c _ {i} $, $ i = 1, 2 , \dots $, $ c _ {0} = 1 $,
$$ U = \mathbf Z [ c _ {1} , c _ {2} , \dots ] . $$
A co-algebra structure is given by
$$ c _ {n} \mapsto \sum _ { p+ q= n} c _ {p} \otimes c _ {q} , $$
and a co-unit by $ \epsilon ( c _ {0} ) = 1 $, $ \epsilon ( c _ {n} ) = 0 $ for $ n \geq 1 $. There is also an antipode, making $ U $ also a graded Hopf algebra. Perhaps the basic result in the representation theory of the symmetric groups is that $ R $ and $ U $ are isomorphic as Hopf algebras. The isomorphism is very nearly unique because, [a1],
$$ \mathrm{Aut} _ { {\rm Hopf} } ( U) = \ \mathbf Z /( 2) \times \mathbf Z / ( 2) . $$
The individual components $ R( S _ {m} ) $ of $ R $ are also rings in themselves under the product of representations $ \rho , \sigma \mapsto \rho \times \sigma $, $ ( \rho \times \sigma ) ( g) = \rho ( g) \otimes \sigma ( g) $. This defines a second multiplication on $ R $, which is distributive over the first, and $ R $ becomes a ring object in the category of co-algebras over $ \mathbf Z $. Such objects have been called Hopf algebras, [a6], and quite a few of them occur naturally in algebraic topology. The ring $ U \simeq R $ occurs in algebraic topology as $ H ^ \star ( \mathbf{BU} ) $, the cohomology of the classifying space $ \mathbf{BU} $ of complex $ K $-theory, and there is a "natural direct isomorphism" $ R \simeq H ^ \star ( \mathbf{BU} ) $, [a3]. (This explains the notation used above for $ U $: the "ci" stand for Chern classes, cf. Chern class.)
There is also an inner product on $ R = U $: $ \langle \rho , \sigma \rangle $ counts the number of irreducible representations that $ \rho $ and $ \sigma $ have in common, and with respect to this inner product $ R $ is (graded) self-dual. In particular, the multiplication and comultiplication are adjoint to one another:
$$ \langle \rho , \sigma \tau \rangle = \ \langle \mu ( \rho ) , \sigma \otimes \tau \rangle , $$
which is the same as Frobenius reciprocity, cf. Induced representation, in this case.
As a coring object in the category of algebras $ U $, being the representing object $ R( W) $ of the functor of Witt vectors, [a2], plays an important role in formal group theory. But, so far, no direct natural isomorphism has been found linking $ R $ with $ U = R( W) $ in this manifestation.
The ring $ U $ also carries the structure of a $ \lambda $-ring and it is in fact the universal $ \lambda $-ring on one generator, $ U( \Lambda ) $, [a4], and this gives a natural isomorphism $ U( \Lambda ) \simeq R( W) $, cf. $ \lambda $-ring for some more details.
Finally there is a canonical notion of positivity on $ \oplus R( S _ {n} ) $: the actual (i.e. not virtual) representations are positive and the multiplication and comultiplication preserve positivity. This has led to the notion of a PSH-algebra, which stands for positive self-adjoint Hopf algebra, [a5]. Essentially, $ U $ is the unique PSH-algebra on one generator and all other are tensor products of graded shifted copies of $ U $. This can be applied to other series of classical groups than the $ S _ {m} $, [a5].
In combinatorics the algebra $ U $ also has a long history. In modern terminology it is at the basis of the so-called umbral calculus, [a7].
A modern reference to the representation theory of the symmetric groups, both ordinary and modular, is [a8].
References
| [a1] | A. Liulevicius, "Arrows, symmetries, and representation rings" J. Pure Appl. Algebra , 19 (1980) pp. 259–273 MR0593256 Zbl 0448.55013 |
| [a2] | M. Hazewinkel, "Formal rings and applications" , Acad. Press (1978) |
| [a3] | M.F. Atiyah, "Power operations in K-theory" Quarterly J. Math. (2) , 17 (1966) pp. 165–193 MR0202130 Zbl 0144.44901 |
| [a4] | D. Knutson, "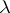 -rings and the representation theory of the symmetric group" , Springer (1973) MR0364425 Zbl 0272.20008 -rings and the representation theory of the symmetric group" , Springer (1973) MR0364425 Zbl 0272.20008 |
| [a5] | A.V. Zelevinsky, "Representations of finite classical groups" , Springer (1981) MR0643482 Zbl 0465.20009 |
| [a6] | D.C. Ravenel, "The Hopf ring for complex cobordism" J. Pure Appl. Algebra , 9 (1977) pp. 241–280 MR0448337 Zbl 0373.57020 |
| [a7] | S. Roman, "The umbral calculus" , Acad. Press (1984) MR0741185 Zbl 0536.33001 |
| [a8] | G. James, A. Kerber, "The representation theory of the symmetric group" , Addison-Wesley (1981) MR0644144 Zbl 0491.20010 |
| [a9] | G. de B. Robinson, "Representation theory of the symmetric group" , Univ. Toronto Press (1961) MR1531490 MR0125885 Zbl 0102.02002 |
| [a10] | J.A. Green, "Polynomial representations of 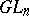 " , Lect. notes in math. , 830 , Springer (1980) MR0606556 Zbl 0451.20037 " , Lect. notes in math. , 830 , Springer (1980) MR0606556 Zbl 0451.20037 |
Representation of the symmetric groups. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Representation_of_the_symmetric_groups&oldid=52077