Rational number
A number expressible as a fraction of integers. The formal theory of rational numbers is developed using pairs of integers. One considers ordered pairs $(a,b)$ of integers $a$ and $b$ for which $b\neq0$. Two such pairs, $(a,b)$ and $(c,d)$, are called equivalent (equal) if and only if $ad=bc$. This is an equivalence relation, being reflexive, symmetric and transitive, and so partitions the set of all such pairs into equivalence classes. A rational number is defined as an equivalence class of pairs. A pair $(a,b)$ is also called a rational fraction (or fraction of integers). Distinct classes define distinct rational numbers. The set of all rational numbers is countable. The rational number containing a pair of the form $0/b$ is called zero. If $r$ is a rational number and $a/b\in r$, then the rational number containing $-a/b$ is called the (additive) inverse of $r$, and is denoted by $-r$. A rational number $r$ is called positive (negative) if it contains a rational fraction $a/b$ with $a$ and $b$ of the same sign (of different signs). If a rational number is positive (negative), then its (additive) inverse is negative (positive). The set of rational numbers can be ordered in the following way: Every negative rational number is less then every positive one, and a positive rational number $r'$ is less than another positive rational number $r''$ (written $r'<r''$) if there exist rational fractions $a/b\in r'$ and $c/d\in r''$, $a,b,c,d>0$, such that $ad>bc$; every negative (positive) rational number $r$ is smaller (greater) then zero: $r<0$ ($r>0$); a negative rational number $r'$ is less than another negative rational number $r''$ if the positive rational number $-r'$ is greater than the positive rational number $-r''$: $-r'>-r''$. The absolute value $|r|$ of a rational number $r$ is defined in the usual way: $|r|=r$ if $r\geq0$ and $|r|=-r$ if $r<0$.
The sum of two rational fractions $a/b$ and $c/d$ is defined as the rational fraction $(ad+bc)/bd$ and the product as $ac/bd$. The sum and product of two rational numbers $r'$ and $r''$ are defined as the equivalence classes of rational fractions containing the sum and product of two rational fractions $a/b$ and $c/d$ belonging to $r'$ and $r''$, respectively. The order, sum and product of rational numbers $r'$ and $r''$ do not depend on the choice of representatives of the corresponding equivalence classes, that is, they are uniquely determined by $r'$ and $r''$ themselves. The rational numbers form an ordered field, denoted by $\mathbf Q$.
A rational number $r$ is denoted by any rational fraction $a/b$ from its equivalence class, i.e. $a/b\in r$. Thus, one and the same rational number can be written as distinct, but equivalent, rational fractions.
If every rational number containing a rational fraction of the form $a/1$ is associated with the integer $a$, then one obtains an isomorphism from the set of such rational numbers onto the ring $\mathbf Z$ of integers. Therefore, the rational number containing a rational fraction of the form $a/1$ is denoted by $a$.
Each function of the form
$$\phi(r)=|r|^\alpha,\quad0<\alpha\leq1,\label{1}\tag{1}$$
is a norm on the field of rational numbers $\mathbf Q$, that is, it satisfies the conditions:
1) $\phi(r)>0$ for any $r\neq0$, $\phi(0)=0$;
2) $\phi(r'+r'')\leq\phi(r')+\phi(r'')$;
3) $\phi(r'\cdot r'')=\phi(r')\phi(r'')$ for all $r',r''\in\mathbf Q$. The field of rational numbers is not complete with respect to the norm \eqref{1}. The completion of $\mathbf Q$ with respect to the norm \eqref{1} yields the field of real numbers.
Consider the function
$$\Psi_p(r)=\rho^{\nu(r)},\label{2}\tag{2}$$
where $p$ is a prime number, $r$ is a rational number and $\nu(r)$ is determined by:
$$r=p^{\nu(r)}\frac ab,$$
where $\nu(r)$ is an integer, $a/b$ is an irreducible rational fraction such that $a$ and $b$ are not divisible by $p$, and $\rho$ is a fixed number, $0<\rho<1$. Then $\Psi_p$ is a norm on $\mathbf Q$. It induces the so-called $p$-adic metric. $\mathbf Q$ is not complete with respect to this metric. By completing $\mathbf Q$ with respect to the norm \eqref{2}, one obtains the field of $p$-adic numbers (cf. $p$-adic number). The metrics induced by \eqref{1} and \eqref{2} (for all prime numbers) exhaust all non-trivial metrics on $\mathbf Q$.
In decimal notation, only rational numbers are representable as periodic decimals fractions.
References
| [1] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1987) (Translated from Russian) (German translation: Birkhäuser, 1966) |
| [2] | C. Pisot, M. Zamansky, "Mathématiques générales: algèbre-analyse" , Dunod (1966) |
Comments
Another property characterizing rational numbers is that their continued fraction is finite. A very important theme in number theory is to find only the rational solutions of equations such as $y^2=x^3-7$, $x^3+y^3+z^3=4$, etc. (see Diophantine equations). Finally, the subject of "rational numbers" is intimately connected with that of irrational numbers (cf. Irrational number). It is not known, for example, whether or not $e\pi$, $e+\pi$ or the Euler constant $\gamma$ are rational.
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapt. XIII |
| [a2] | G. Bachman, "Introduction to 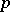 -adic numbers and valuation theory" , Acad. Press (1964) -adic numbers and valuation theory" , Acad. Press (1964) |
| [a3] | B.L. van der Waerden, "Algebra" , 2 , Springer (1971) (Translated from German) |
Rational number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rational_number&oldid=44709