Quasi-conformal mapping
A mapping with bounded distortion or bounded deviation from a conformal mapping. A numerical characterization of the distortion under a mapping $ f : D \rightarrow D ^ \prime $
at a point $ a \in D $
is the coefficient $ k ( f , a ) $
of quasi-conformality (dilatation or dilation) of $ f $
at this point:
$$ k ( f , a ) = \ {\lim\limits \sup } _ {r \rightarrow 0 } \ \frac{\sup _ {| x - a | = r } | f ( x) - f ( a) | }{\inf _ {| x - a | = r } | f ( x) - f ( a ) | } . $$
The quantity
$$ k ( f ) = \ \left \{ \begin{array}{lll} \infty & {\textrm{ if } } &{\sup _ {x \in D } k( f, x) = \infty , } \\ { \mathop{\rm esssup} _ {x \in D } k( f, x) } & {\textrm{ if } } &{\sup _ {x \in D } k( f, x) < \infty , } \\ \end{array} \right .$$
is called the coefficient of quasi-conformality (or linear dilatation) of $ f $ in the domain $ D $. An orientation-preserving mapping $ f : D \rightarrow D ^ \prime $ is called quasi-conformal (or a mapping with bounded distortion) if $ k ( f ) < \infty $; it is called $ k $- quasi-conformal if $ k ( f ) \leq k $. For a conformal mapping $ k ( f ) = 1 $. If $ f $ is differentiable at the point $ a \in D $, then the linear mapping $ f ^ { \prime } ( a) $ transforms a ball of the tangent space into an ellipsoid the ratio of the major to the minor semi-axis of which is $ k ( f , a ) $.
Along with the given definition, one often uses the following, equivalent, conditions of quasi-conformality of $ f $ in a domain $ D \subset \mathbf R ^ {n} $: $ f \in W _ {n} ^ {1} $( that is, $ f $ has generalized derivatives that are locally $ n $- th power summable in $ D $) and there exists a real number $ k $ such that
$$ \| f ^ { \prime } ( x) \| ^ {n} \ \leq k \mathop{\rm det} f ^ { \prime } ( x) , $$
or
$$ | \mathop{\rm grad} f ( x) | ^ {n} \ \leq k n ^ {n/2} \mathop{\rm det} f ^ { \prime } ( x) $$
for almost-all points $ x \in D $.
The term "quasi-conformal mapping" , as a rule, presupposes the mapping to be a homeomorphism. Non-homeomorphisms with bounded distortion are usually called quasi-regular mappings. The theory of quasi-conformal mappings of domains in $ \mathbf R ^ {n} $ for $ n = 2 $ and for $ n \geq 3 $, provided that one is not considering general and, as a rule, simple questions for them, has sharp differences.
Two-dimensional theory.
In this case the differential of a mapping at a point $ z \in D $ can be written in the form
$$ d f ( z) = f _ {z} ( z) d z + f _ {\overline{z}\; } ( z) d \overline{z}\; . $$
It is defined up to a factor by the formula
$$ \tag{1 } f _ {\overline{z}\; } ( z) = \mu ( z) f _ {z} ( z) . $$
The function $ \mu ( z) $ is called the Beltrami coefficient, the complex dilatation or the complex characteristic of the mapping $ f $ at the point $ z $; $ | \mu ( z) | < 1 $ for a mapping with a positive Jacobian $ J = | f _ {z} | ^ {2} - | f _ {\overline{z}\; } | ^ {2} $. For analytic mappings $ \mu ( z) \equiv 0 $, which are the Cauchy–Riemann conditions. The coefficient $ k ( f , z ) $ of quasi-conformality of a mapping at a point is expressed in terms of $ \mu ( z) $ by
$$ k ( f , z ) = \ \frac{1 + | \mu ( z) | }{1 - | \mu ( z) | } , $$
therefore the condition of quasi-conformality of an $ f \in W _ {2} ^ {1} $ in terms of the complex characteristic is $ \| \mu \| _ \infty ( D) < 1 $.
Usually formula (1) appears as an equation in $ f $ with a known function $ \mu $; it is called the Beltrami equation (or Beltrami system). For example, the problem of conformally mapping one domain $ D $ onto another $ D ^ \prime $ is the problem of seeking a homeomorphism $ f : D \rightarrow D ^ \prime $ that satisfies the Beltrami equation in $ D $ with $ \mu ( z) \equiv 0 $.
An example of a problem that reduces to the solution of the general equation (1) is the classical Gauss problem of the simultaneous reduction to canonical form in all of a given domain $ D $ of a positive-definite quadratic form in two variables, or, what is the same, the problem of constructing conformally-Euclidean coordinates on a two-dimensional surface (see [50]).
The basic fact [5], [30] of the two-dimensional theory of quasi-conformal mappings, analogous to the Riemann mapping theorem, (cf. Riemann theorem), is called the measurable Riemann mapping theorem and consists in the following. For each measurable function $ \mu ( z) $ in a domain $ D \subset \overline{ {\mathbf C }}\; $ such that $ \| \mu \| _ \infty ( D) < 1 $, find a quasi-conformal homeomorphism $ f $ of $ D $ with complex characteristic $ \mu ( z) $; the general solution of equation (1) in $ D $ has the form $ F \circ f ( z) $, where $ f $ is the to be constructed quasi-conformal homeomorphism and $ F $ is any analytic function.
If $ D $ is the unit disc, $ f $ can be chosen so that $ f ( D) = D $. Then $ f $ can be extended to a homeomorphism of the closed disc onto itself and the normalization conditions $ f ( 0) = 0 $, $ f ( 1) = 1 $ select a unique homeomorphism $ f : D \rightarrow D $ satisfying the Beltrami equation. If, in addition, $ \mu \in C _ \alpha ^ {m} ( D) $, $ 0 < \alpha < 1 $, $ m \geq 0 $, then $ f \in C _ \alpha ^ {m+} 1 ( D) $, where $ C _ \alpha ^ {m} ( D) $ is the space of functions that have $ m $ continuous derivatives in $ D $, the highest being Hölder continuous in $ D $ of order $ \alpha $( cf. Hölder condition). If a sequence $ f _ {n} $ of normalized quasi-conformal automorphisms of the disc $ D $ is such that $ | \mu _ {n} ( z) | \leq \mu < 1 $ and $ \| \mu _ {n} \| _ \infty ( D) \rightarrow 0 $ as $ n \rightarrow \infty $, then
$$ \| f _ {n} ( z) - z \| _ {C ( D) } \rightarrow 0 . $$
Quasi-conformal mappings as homeomorphic solutions of strongly-elliptic systems
$$ \tag{2 } \Phi _ {i} ( x , y , u , v , u _ {x} , u _ {y} , v _ {x} , v _ {y} ) \ = 0 ,\ i = 1 , 2 , $$
are also naturally connected with problems on streamline flows of subsonic gas dynamics, just as conformal mappings satisfying the Cauchy–Riemann system are connected with the flow of an incompressible ideal fluid (see [9], [31]).
The general problem of constructing a quasi-conformal mapping from one simply-connected domain onto another satisfying (2) was posed and solved by M.A. Lavrent'ev [28], [31], one of the founders of the theory of quasi-conformal mappings. Quasi-conformal mappings appeared in explicit form in the works of H. Grötzsch (see [23], [24]). In particular, he considered [24] the following extremal problem (Grötzsch' problem, [2]): To find among the mappings taking the vertices of a square to vertices of a rectangle that is not a square, a mapping that is nearest to a conformal one. In order to characterize the measure of this closeness it was necessary to introduce the coefficient of quasi-conformality, an initial concept in the geometric theory of quasi-conformal mappings. These mappings occurred later under the name quasi-conformal in the paper [1] by L.V. Ahlfors on covering surfaces. In the late 1930's O. Teichmüller vastly extended the study of Grötzsch to mappings between closed Riemann surfaces and obtained a natural parameter space for such surfaces of fixed genus [44] (the so-called Teichmüller space). In recent years Ahlfors, L. Bers [6], their school, and successors have greatly expanded Teichmüller's theory [3], [10], [14]. Two-dimensional quasi-conformal mappings have found new beautiful applications in geometric function theory (uniformization, moduli, Kleinian groups [11], [43], Nevanlinna theory [18]), in topology (Thurston theory, [12], [13]) and in topological dynamics (Fatou–Julia problem, [42]).
In the two-dimensional theory of quasi-conformal mappings, as in the theory of analytic functions, general questions of compactness are studied, that is, normal families of mappings, a theory of boundary correspondence has been constructed by showing that this correspondence is realized in terms of the same Carathéodory prime ends (see Limit elements) as in the conformal case; conditions for the removability of singularity sets have been studied; and variational principles have been developed for the solution of fundamental extremal problems in the class of quasi-conformal homeomorphisms (see [7], [26], [27]).
Spatial theory.
The theory of quasi-conformal mappings of domains in a space $ \mathbf R ^ {n} $, $ n \geq 3 $, also has its own features. This is first of all connected with the absence of conformal mappings: according to Liouville's theorem, every sufficiently smooth conformal mapping of a domain $ D \subset \mathbf R ^ {n} $, $ n \geq 3 $, is a Möbius transformation, that is, a superposition of an inversion and a rotation. The essence of this fact is that the condition of conformality of a mapping when $ n \geq 3 $, in contrast to the Cauchy–Riemann conditions for $ n = 2 $, consists of an overdetermined system of partial differential equations.
Some important results of the spatial theory of quasi-conformal mappings are indicated below. Liouville's theorem is valid both in the case of Hilbert space [36] and under minimal a priori regularity conditions on the mapping [19], [38]. In Liouville's theorem there is stability ([8], [38]), in the sense that there exist constants $ k _ {1} $ and $ k _ {2} $ and a function $ \lambda ( \epsilon ) = O ( \epsilon ) $, as $ \epsilon \rightarrow 0 $, with the following properties: a) if $ y = f ( x) $ is a quasi-conformal mapping of the ball $ | x | < 1 $ with $ k ( f ) < k _ {1} $, then there exists a Möbius transformation $ L ( y) $ such that
$$ \sup _ {| x | < 1 } | L \circ f ( x) | < \infty , $$
and the image of the unit ball under $ L \circ f $ contains the ball $ | y | < 1 $; b) if $ k ( f ) \leq 1 + \epsilon < k _ {2} $, then
$$ | L \circ f ( x _ {1} ) - L \circ f ( x _ {2} ) | \ \leq k ( \epsilon ) \ | x _ {1} - x _ {2} | ^ {\alpha ( \epsilon ) } , $$
where
$$ \lim\limits _ {\epsilon \rightarrow 0 } k ( \epsilon ) = 1 \ \ \textrm{ and } \ \lim\limits _ {\epsilon \rightarrow 0 } \alpha ( \epsilon ) = 1 ; $$
c) if $ k ( f ) \leq 1 + \epsilon $, then
$$ | L \circ f ( x) - x | \leq \lambda ( \epsilon ) $$
throughout the ball $ | x | < 1 $. Stability also holds in certain classes of domains with a non-regular boundary, and also in the sense of different norms [38]. At present (1990), stability estimates have been established for dimension $ n \geq 3 $, with $ n $ finite and fixed (i.e. $ k, \alpha , \lambda $ are also functions of $ n $).
In the same way that a $ 1 $- quasi-conformal mapping turns out to be a Möbius transformation even without the a priori assumption that it is a homeomorphism, a quasi-conformal mapping is locally homeomorphic as soon as its coefficient of quasi-conformality is sufficiently close to 1 [22], [34]. In contrast to the planar case, every locally homeomorphic quasi-conformal mapping of the unit ball in $ \mathbf R ^ {n} $, $ n \geq 3 $, is automatically homeomorphic in some ball $ | x | \leq r ( n , k ) < 1 $, where $ r $ depends only on the dimension $ n $ of the space and the coefficient of quasi-conformality $ k = k ( f ) $ of the mapping [34]. In particular, a locally homeomorphic quasi-conformal mapping $ f $ of the whole space $ \mathbf R ^ {n} $, $ n \geq 3 $, is globally homeomorphic, and $ f ( \mathbf R ^ {n} ) = \mathbf R ^ {n} $[39], [52]. Boundary behaviour: If $ f : \mathbf R _ {+} ^ {n} \rightarrow \mathbf R _ {+} ^ {n} $ is a quasi-conformal mapping of the half-space $ x _ {n} > 0 $ of $ \mathbf R ^ {n} $, $ n \geq 2 $, onto itself, then $ f $ can be extended to a homeomorphism of the closed domains; here the induced homeomorphism $ \phi : \mathbf R ^ {n-} 1 \rightarrow \mathbf R ^ {n-} 1 $ on the boundary $ \partial \mathbf R _ {+} ^ {n} = \mathbf R ^ {n-} 1 $ satisfies for the case $ n = 2 $ the $ M $- condition [15]:
$$ M ^ {-} 1 \leq \ \frac{\phi ( x + h ) - \phi ( x) }{\phi ( x) - \phi ( x - h ) } \leq M , $$
and in the case $ n \geq 3 $ it is quasi-conformal [19]. Each of these last two conditions on the dimension is not only necessary but also sufficient in order that a mapping $ \phi : \partial \mathbf R _ {+} ^ {n} \rightarrow \mathbf R _ {+} ^ {n} $ be the boundary trace of some quasi-conformal mapping [45]–[47].
The possibility arising from this of extending a quasi-conformal automorphism of Lobachevskii space to a quasi-conformal mapping of the absolute of this space, in accordance with the fact that a $ 1 $- quasi-conformal mapping of the sphere is conformal and is the trace of a conformal automorphism of the ball, lies at the basis of the proof of the rigidity of spatial hyperbolic forms: If two closed Riemannian manifolds of dimension $ n \geq 3 $ and of the same constant negative curvature are homeomorphic, then they are isometric (see [35], [41]).
The normality property and the character of convergence of quasi-conformal mappings made it possible, on the one hand, to establish the Carathéodory convergence theorem for quasi-conformal mappings [20] and, on the other hand, to apply the mappings to the positive solution of the Lichnerowicz conjecture: The conformal group of automorphisms of a compact Riemannian manifold is not compact if and only if the manifold is a sphere [33].
A lot of results in the theory concern quasi-regular (i.e. non-homeomorphic quasi-conformal) mappings [34], [37]. An advanced theory of value distribution has been worked out for such mappings. Also, a theorem of Picard type has been proved, and it happens that the possibility of omitting a finite number of points in $ \mathbf R ^ {n} $ for $ n \geq 3 $ depends on the coefficient of quasi-conformality of the mapping [39], [40].
A concise exhaustive presentation of the theory of quasi-conformal mappings in dimension $ n = 2 $ can be found in [2], [32]; references [37], [48], [16], [19] are devoted to the case $ n \geq 3 $. One can find a large bibliography in [17] and in the more recent monograph [51]. Articles [3], [21], [49] are survey reports at international mathematical congresses.
References
| [1] | L.V. Ahlfors, "Zur Theorie der Überlagerungsflächen" Acta Math. , 65 (1935) pp. 157–194 |
| [2] | L.V. Ahlfors, "Lectures on quasi-conformal mappings" , v. Nostrand (1966) |
| [3] | L.V. Ahlfors, "Quasi-conformal mappings, Teichmüller spaces and Kleinian groups" , Proc. Internat. Congress Mathematicians (Helsinki, 1978) , Acad. Sci. Fennicae (1980) pp. 71–84 |
| [4] | L.V. Ahlfors, "Möbius transformations in several dimensions" , Univ. Minnesota (1981) |
| [5] | L.V. Ahlfors, L. Bers, "Riemann's mapping theorem for variable metrics" Ann. of Math. (2) , 72 (1960) pp. 385–404 |
| [6] | L.V. Ahlfors, L. Bers, "Spaces of Riemann surfaces and quasi-conformal mappings" , Moscow (1961) (In Russian) |
| [7] | P.P. Belinskii, "General properties of quasi-conformal mappings" , Novosibirsk (1974) (In Russian) |
| [8] | P.P. Belinskii, "On the order of closeness of a spatial quasi-conformal mapping to conformal" Sibir. Math. J. , 14 : 3 (1974) pp. 325–331 Sibirsk. Mat. Zh. , 14 : 3 (1973) pp. 475–483 |
| [9] | L. Bers, "Mathematical aspects of subsonic and transonic gas dynamics" , Chapman & Hall (1958) |
| [10] | L. Bers, "Quasi-conformal mappings and Teichmüller's theorem" R. Nevanlinna (ed.) et al. (ed.) , Analytic functions , Princeton Univ. Press (1960) pp. 89–119 |
| [11] | L. Bers, "Uniformization, moduli and Kleinian groups" Bull. London Math. Soc. , 4 (1972) pp. 257–300 |
| [12] | L. Bers, "Quasi-conformal mappings with applications to differential equations, function theory and topology" Bull. Amer. Math. Soc. , 83 (1977) pp. 1083–1100 |
| [13] | L. Bers, "An extremal problem for quasi-conformal mappings and a problem of Thurston" Acta Math. , 141 (1978) pp. 73–98 |
| [14] | L. Bers, "Finite dimensional Teichmüller spaces and generalizations" Bull. Amer. Math. Soc. , 5 (1981) pp. 131–172 |
| [15] | A. Beurling, L.V. Ahlfors, "The boundary correspondence under quasi-conformal mappings" Acta Math. , 96 (1956) pp. 125–142 |
| [16] | B. Bojarski, T. Ivaniec, "Analytical foundations of the theory of quasi-conformal mappings in 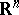 " Ann. Acad. Sci. Fenn. Ser. AI Math. , 8 (1983) pp. 257–324 " Ann. Acad. Sci. Fenn. Ser. AI Math. , 8 (1983) pp. 257–324 |
| [17] | P. Caraman, " -dimensional quasi-conformal (Qcf) mappings" , Ed. Acad. Romania & Abacus Press (1974) -dimensional quasi-conformal (Qcf) mappings" , Ed. Acad. Romania & Abacus Press (1974) |
| [18] | D. Drasin, "The inverse problem of Nevanlinna theory" Acta Math. , 138 (1977) pp. 83–151 |
| [19] | F.W. Gehring, "Rings and quasiconformal mappings in space" Trans. Amer. Math. Soc. , 103 (1962) pp. 353–393 |
| [20] | F.W. Gehring, "The Carathéodory convergence theorem for quasiconformal mappings in space" Ann. Acad. Sci. Fenn. Ser. AI Math. , 336 : 11 (1964) pp. 1–21 |
| [21] | F.W. Gehring, "Topics in quasiconformal mappings" , Proc. Internat. Congress Mathematicians (Berkeley, 1986) , Amer. Math. Soc. (1987) pp. 62–80 |
| [22] | V.M. Gol'dshtein, "The behavior of mappings with bounded distortion when the coefficient of distortion is close to unity" Siber. Math. J. , 12 : 6 (1971) pp. 900–907 Sibirsk. Mat. Zh. , 12 : 6 (1971) pp. 1250–1259 |
| [23] | H. Grötzsch, "Über die Verzerrung bei schlichten nichtkonformen Abbildungen und über eine damit zusammenhängende Erweiterung des Picardschen Satzes" Ber. Verh. Sächs. Akad. Wiss. Leipzig , 80 (1928) pp. 503–507 |
| [24] | H. Grötzsch, "Über möglichst konforme Abbildungen von schlichten Bereichen" Ber. Verh. Sächs. Akad. Wiss. Leipzig , 84 (1932) pp. 114–120 |
| [25] | I. Kra, "On the Nielsen–Thurston–Bers type of some self-maps of Riemann surfaces" Acta Math. , 146 (1981) pp. 231–270 |
| [26] | S.L. Krushkal', "Quasi-conformal mappings and Riemann surfaces" , Winston (1979) (Translated from Russian) |
| [27] | S.L. Krushkal', R. Kühnau, "Quasi-konforme Abbildungen - neue Methoden und Anwendungen" , Teubner (1983) |
| [28] | M. [M.A. Lavrent'ev] Lavrentieff, "Sur une classe de réprésentation continues" Rec. Math. , 42 (1935) pp. 407–424 |
| [29] | M. [M.A. Lavrent'ev] Lavrentieff, "Sur une critère différentiel des transformation homéomorphes des domaines à trois dimensions" Dokl. Akad. Nauk SSSR , 20 (1938) pp. 241–242 |
| [30] | M. [M.A. Lavrent'ev] Lavrentieff, "The main theorem of the theory of quasi-conformal mappings of plain domains" Izv. Akad. Nauk SSSR , 12 (1948) pp. 513–554 (In Russian) |
| [31] | M.A. Lavrent'ev, "Variational methods for boundary value problems for systems of elliptic equations" , Noordhoff (1963) (Translated from Russian) |
| [32] | O. Lehto, K.I. Virtanen, "Quasiconformal mappings in the plane" , Springer (1973) |
| [33] | J. Lelong-Ferrand, "Transformations conformes et quasiconformes des variétés Riemanniennes compactes (Démonstration de la conjecture de A. Lichnerowicz)" Acad. Roy. Belg. Cl. Sci. Mém. Collect. , 39 (1971) pp. 1–44 |
| [34] | O. Martio, S. Rickman, J. Väisälä, "Topological and metric properties of quasiregular mappings" Ann. Acad. Sci. Fenn. Ser. AI Math. , 488 (1971) pp. 1–31 |
| [35] | G.D. Mostow, "Quasiconformal mappings in  -space and the rigidity of hyperbolic space forms" Publ. Math. IHES , 34 (1968) pp. 53–104 -space and the rigidity of hyperbolic space forms" Publ. Math. IHES , 34 (1968) pp. 53–104 |
| [36] | R. Nevanlinna, "On differentiable mappings" R. Nevanlinna (ed.) et al. (ed.) , Analytic functions , Princeton Univ. Press (1960) pp. 3–9 |
| [37] | Yu.G. Reshet'nyak, "Space mappings with bounded distortion" , Amer. Math. Soc. (1989) (Translated from Russian) |
| [38] | Yu.G. Reshet'nyak, "Stability theorems in geometry and analysis" , Novosibirsk (1982) (In Russian) |
| [39] | S. Rickman, "On the number of omitted values of entire quasiregular mappings" J. d'Anal. Math. , 37 (1980) pp. 100–117 |
| [40] | S. Rickman, "The analogue of Picard's theorem for quasiregular mappings in dimension three" Acta Math. , 154 (1985) pp. 195–242 |
| [41] | D. Sullivan, "On the ergodic theory at infinity of an arbitrary discrete group of hyperbolic motions" I. Kra (ed.) B. Maskit (ed.) , Riemann Surfaces and Related Topics (Proc. 1978 Stony Brook Conf.) , Princeton Univ. Press (1981) pp. 465–496 |
| [42] | D. Sullivan, "Quasi-conformal homeomorphisms and dynamics I. Solution of the Fatou–Julia problem on wandering domains" Ann. of Math. , 122 (1985) pp. 401–418 |
| [43] | D. Sullivan, "Quasiconformal homeomorphisms and dynamics II. Structural stability implies hyperbolicity for Kleinian groups" Acta Math. , 155 (1985) pp. 243–260 |
| [44] | O. Teichmüller, "Extremale quasikonforme Abbildungen und quadratische Differentiale" Abh. Preuss. Akad. Wiss. Math.-Nat. Kl. , 22 (1940) pp. 1–197 |
| [45] | P. Tukia, "Quasiconformal extension of quasisymmetric mappings compatible with a Möbius group" Acta Math. , 154 (1985) pp. 153–193 |
| [46] | P. Tukia, J. Väisälä, "Quasiconformal extension from dimension  to to 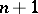 " Ann. of Math. , 115 (1982) pp. 331–348 " Ann. of Math. , 115 (1982) pp. 331–348 |
| [47] | P. Tukia, J. Väisälä, "Bilipschitz extensions of maps having quasiconformal extensions" Math. Ann. , 269 (1984) pp. 561–572 |
| [48] | J. Väisälä, "Lectures on  -dimensional quasiconformal mappings" , Lect. notes in math. , 229 , Springer (1971) -dimensional quasiconformal mappings" , Lect. notes in math. , 229 , Springer (1971) |
| [49] | J. Väisälä, "A survey of quasiregular maps in 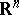 " , Proc. Internat. Congress Mathematicians (Helsinki, 1978) , Acad. Sci. Fennicae (1980) pp. 685–691 " , Proc. Internat. Congress Mathematicians (Helsinki, 1978) , Acad. Sci. Fennicae (1980) pp. 685–691 |
| [50] | I.N. Vekua, "Generalized analytic functions" , Pergamon (1962) (Translated from Russian) |
| [51] | M. Vuorinen, "Conformal geometry and quasiregular mappings" , Lect. notes in math. , 1319 , Springer (1988) |
| [52] | V.A. Zorich, "A theorem of M.A. Lavrent'ev on quasiconformal space maps" Math. USSR Sb. , 3 : 3 (1976) pp. 389–403 Mat. Sb. , 74 (1967) pp. 417–433 |
Comments
The measurable Riemann mapping theorem was proved first by C.B. Morrey in [a1]. The important paper [5] of L.V. Ahlfors and L. Bers shows that if $ \mu ( x) $ depends in a continuous (or continuously differentiable, or real analytic, or complex analytic) fashion on a parameter $ t $, then $ f $, the solution of the Beltrami equation (1), does so as well.
References
| [a1] | C.B. Morrey, "On the solutions of quasilinear elliptic partial differential equations" Trans. Amer. Math. Soc. , 43 (1938) pp. 126–166 |
| [a2] | V. Gol'dshtein, Yu.G. Reshet'nyak, "Quasiconformal mappings and Sobolev spaces" , Kluwer (1990) (Translated from Russian) |
Quasi-conformal mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-conformal_mapping&oldid=49541