Orlicz space
A Banach space of measurable functions introduced by W. Orlicz [1]. Let $ M( u) $
and $ N( u) $
be a pair of complementary $ N $-
functions (see Orlicz class) and let $ G $
be a bounded closed set in $ \mathbf R ^ {n} $.
The Orlicz space $ L _ {M} ^ \star $
is the set of Lebesgue-measurable functions $ x $
on $ G $
for which
$$ \| x \| _ {M} = \sup \left \{ {\int\limits _ { G } x( t) y( t) dt } : { \int\limits _ { G } N( y( t)) dt \leq 1 } \right \} < \infty . $$
An Orlicz space is a complete normed space with respect to the norm $ \| x \| _ {M} $, which is called the Orlicz norm. When $ M( u) = u ^ {p} $, $ 1 < p < \infty $, $ L _ {M} ^ \star $ coincides with the Riesz space $ L _ {p} $ and, up to a scalar factor, $ \| x \| _ {L _ {p} } $ coincides with $ \| x \| _ {M} $.
If $ M _ {1} ( u) $ and $ M _ {2} ( u) $ are $ N $- functions, then the inclusion $ L _ {M _ {1} } ^ \star \subset L _ {M _ {2} } ^ \star $ holds if and only if, for a certain $ C $ and all sufficiently large $ u $, the inequality $ M _ {2} ( u) \leq M _ {1} ( Cu) $ is fulfilled. For every Orlicz space $ L _ {M} ^ \star $ the inclusions $ L _ \infty \subset L _ {M} ^ \star \subset L _ {1} $ hold. Every summable function belongs to some Orlicz space.
The space $ L _ {M} ^ \star $ is separable if and only if $ M( u) $ satisfies the $ \Delta _ {2} $- condition (cf. Orlicz class). In general, $ L _ \infty $ is not dense in $ L _ {M} ^ \star $, and the closure of $ L _ \infty $ in $ L _ {M} ^ \star $ is denoted by $ E _ {M} $ and is always separable. If $ x \in L _ {M} ^ \star $, then
$$ \lim\limits _ {\tau \rightarrow \infty } \sup _ {mes( E) = \tau } \| x {\chi _ {E} } \| _ {M} = \rho ( x, E _ {M} ), $$
where
$$ \chi _ {E} ( t) = \left \{ \begin{array}{ll} 1 , & t \in E, \\ 0, & t \notin E. \\ \end{array} \right .$$
If $ M( u) $ and $ N( u) $ are complementary $ N $- functions and $ x \in L _ {M} ^ \star $, $ y \in L _ {M} ^ \star $, then the following analogue of the Hölder inequality holds:
$$ \int\limits _ { G } x( t) y( t) dt \leq \| x \| _ {(} M) \| y \| _ {(} N) , $$
where $ \| x \| _ {(} M) $ is the Luxemburg norm. Every continuous linear functional $ f $ on $ E _ {M} $ can be represented in the form
$$ f( x) = \int\limits _ { G } x( t) y( t) dt, $$
where $ y \in L _ {N} $ and $ \| f \| = \| y \| _ {(} N) $.
The compactness criteria of M. Riesz and A.N. Kolmogorov for the spaces $ L _ {p} $ can also be applied to $ E _ {M} $. The following conditions are equivalent:
1) the space $ L _ {M} ^ \star $ is reflexive;
2) $ M( u) $ and $ N( u) $ satisfy the $ \Delta _ {2} $- condition;
3) an unconditional basis exists in $ L _ {M} ^ \star $;
4) the Haar system forms an unconditional basis in $ L _ {M} ^ \star $;
5) the trigonometric system is a basis in $ L _ {M} ^ \star $ and the Haar system is a basis in $ E _ {M} $.
A sequence space $ l _ {M} ^ \star $ is defined in the same way, but the properties of $ l _ {M} ^ \star $ depend on the asymptotics of the function $ M( u) $ at 0. Many of the geometric properties of $ L _ {M} ^ \star $ and $ l _ {M} ^ \star $ are studied in [5]; for example, for any function $ M( u) $, the set of all $ p $ such that $ l _ {p} $ is isomorphically imbeddable in $ L _ {M} ^ \star $ can be found.
Orlicz spaces are used in the study of the properties of integral operators, the theory of differentiable functions of several variables and in other areas of analysis.
References
| [1] | W. Orlicz, "Ueber eine gewisse Klasse von Räumen vom Typus 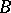 " Bull. Intern. Acad. Pol. Ser. A , 8/9 (1932) pp. 207–220 " Bull. Intern. Acad. Pol. Ser. A , 8/9 (1932) pp. 207–220 |
| [2] | M.A. Krasnosel'skii, Ya.B. Rutitskii, "Convex functions and Orlicz spaces" , Noordhoff (1961) (Translated from Russian) |
| [3] | V.F. Gaposhkin, "Existence of absolute bases in Orlicz spaces" Funct. Anal. Appl. , 1 : 4 (1967) pp. 278–284 Funkts. Anal. i Prilozhen. , 1 : 4 (1967) pp. 26–32 |
| [4] | S.G. Krein, Yu.I. Petunin, E.M. Semenov, "Interpolation of linear operators" , Amer. Math. Soc. (1982) (Translated from Russian) |
| [5] | J. Lindenstrauss, L. Tzafriri, "Classical Banach spaces" , 1–2 , Springer (1977–1979) |
Comments
References
| [a1] | W.A.J. Luxemburg, A.C. Zaanen, "Riesz spaces" , I , North-Holland (1971) |
Orlicz space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Orlicz_space&oldid=49503