Integral cosine
The special function defined, for real $ x > 0 $,
by
$$ \mathop{\rm Ci} ( x) = - \int\limits _ { x } ^ \infty \frac{\cos t }{t } \ d t = c + \mathop{\rm ln} x - \int\limits _ { 0 } ^ { x } \frac{1 - \cos t }{t } \ d t , $$
where $ c = 0.5772 \dots $ is the Euler constant. Its graph is:
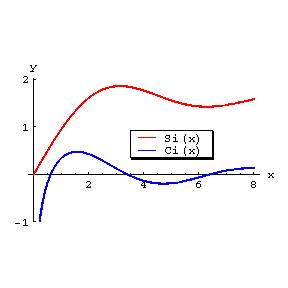
Figure: i051370a
The graphs of the functions $ y = \mathop{\rm ci} ( x) $ and $ y = \mathop{\rm si} ( x) $.
Some integrals related to the integral cosine are:
$$ \int\limits _ { 0 } ^ \infty e ^ {- p t } \mathop{\rm Ci} ( q t ) d t = - \frac{1}{2p} \mathop{\rm ln} \left ( 1 + \frac{p ^ {2} }{q ^ {2} } \right ) , $$
$$ \int\limits _ { 0 } ^ \infty \cos t \mathop{\rm Ci} ( t) \ d t = - \frac \pi {4} ,\ \int\limits _ { 0 } ^ \infty \mathop{\rm Ci} ^ {2} ( t) d t = \frac \pi {2} , $$
$$ \int\limits _ { 0 } ^ \infty \mathop{\rm Ci} ( t) \mathop{\rm si} ( t) d t = - \mathop{\rm ln} 2 , $$
where $ \mathop{\rm si} ( t) $ is the integral sine minus $ \pi / 2 $.
For $ x $ small:
$$ \mathop{\rm Ci} ( x) \approx c + \mathop{\rm ln} x . $$
The asymptotic representation, for $ x $ large, is:
$$ \mathop{\rm Ci} ( x) = \ \frac{\sin x }{x} P ( x) - \frac{\cos x }{x} Q ( x) , $$
$$ P ( x) \sim \sum_{k=0}^ \infty \frac{( - 1 ) ^ {k} ( 2 k ) ! }{x ^ {2k} } ,\ Q ( x) \sim \sum_{k=0}^ \infty \frac{( - 1 ) ^ {k} ( 2 k + 1 ) ! }{x ^ {2k+1} } . $$
The integral cosine has the series representation:
$$ \tag{* } \mathop{\rm Ci} ( x) = c + \mathop{\rm ln} x - \frac{x ^ {2} }{2!2} + \frac{x ^ {4} }{4!4} - \dots + $$
$$ + ( - 1 ) ^ {k} \frac{x ^ {2k} }{( 2 k ) ! 2 k } + \dots . $$
As a function of the complex variable $ z $, $ \mathop{\rm Ci} ( z) $, defined by (*), is a single-valued analytic function in the $ z $- plane with slit along the relative negative real axis $ ( - \pi < \mathop{\rm arg} z < \pi ) $. The value of $ \mathop{\rm ln} z $ here is taken to be $ \pi < \mathop{\rm Im} \mathop{\rm ln} z < \pi $. The behaviour of $ \mathop{\rm Ci} ( z) $ near the slit is determined by the limits
$$ \lim\limits _ {\eta \downarrow 0 } \mathop{\rm Ci} ( x \pm i \eta ) = \ \mathop{\rm Ci} ( | z | ) \pm \pi i ,\ x < 0 . $$
The integral cosine is related to the integral exponential function $ \mathop{\rm Ei} ( z) $ by
$$ \mathop{\rm Ci} ( z) = \frac{1}{2} [ \mathop{\rm Ei} ( i z ) + \mathop{\rm Ei} ( - i z ) ] . $$
One sometimes uses the notation $ \mathop{\rm ci} ( x) \equiv \mathop{\rm Ci} ( x) $.
See also Si-ci-spiral.
References
| [1] | H. Bateman (ed.) A. Erdélyi (ed.) et al. (ed.) , Higher transcendental functions , 2. Bessel functions, parabolic cylinder functions, orthogonal polynomials , McGraw-Hill (1953) |
| [2] | E. Jahnke, F. Emde, "Tables of functions with formulae and curves" , Dover, reprint (1945) (Translated from German) |
| [3] | A. Kratzer, W. Franz, "Transzendente Funktionen" , Akademie Verlag (1960) |
| [4] | N.N. Lebedev, "Special functions and their applications" , Prentice-Hall (1965) (Translated from Russian) |
Comments
The function $\mathop{\rm Ci}$ is better known as the cosine integral. It can, of course, be defined by the integral (as above) in $ \mathbf C \setminus \{ {x \in \mathbf R } : {x \leq 0 } \} $.
Integral cosine. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_cosine&oldid=54982