Cantor ternary function

2020 Mathematics Subject Classification: Primary: 26A45 Secondary: 28A15 [MSN][ZBL]

The Cantor ternary function (also called Devil's staircase and, rarely, Lebesgue's singular function) is a continuous monotone function $f$ mapping the interval $[0,1]$ onto itself, with the remarkable property that its derivative vanishes almost everywhere (recall that any monotone function is differentiable almost everywhere, see for instance Function of bounded variation).

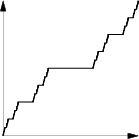
The function can be defined in the following way (see, for example, Exercise 46 in Chapter 2 of [Ro]). Given $x\in [0,1]$ consider its ternary expansion $\{a_i\}$, i.e. a choice of coefficients $a_i\in \{0,1,2\}$ such that \[ x = \sum_{i=1}^\infty \frac{a_i}{3^i}\, . \] Define $n(x)$ to be

• $\infty$ if none of the coefficients $a_i$ takes the value $1$
• the smallest integer $n$ such that $a_n=1$ otherwise.

Then \[ f(x) = \sum_{i=1}^{n(x)-1} \frac{a_i}{2^{i+1}} + \frac{1}{2^{n(x)}}. \] For alternative definitions see Example 1.67 of [AFP] and page 55 of [Co].

It follows trivially from the definition that $f$ is locally constant on the complement of the Cantor set $C$: since the Cantor set is a set of Lebesgue measure zero, the derivative of $f$ vanishes almost everywhere. For the same reason, the distributional derivative of $f$ is a singular measure $\mu$ supported on $C$.

The Cantor function is a prototype of a singular function in the sense of Lebesgue, cf. Lebesgue decomposition. The observation that $f$ is a function of bounded variation for which \[ f (1)-f(0) \neq \int_0^a f'(t)\, dt \] (where $f'$ denotes the classical pointwise derivative) was first made by Vitali in [Vi]. For this reason some authors use the terminology Cantor-Vitali function (see [AFP]).

References

[AFP]	L. Ambrosio, N. Fusco, D. Pallara, "Functions of bounded variations and free discontinuity problems". Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press, New York, 2000. MR1857292Zbl 0957.49001
[Co]	D. L. Cohn, "Measure theory". Birkhäuser, Boston 1993.
[Ro]	H.L. Royden, "Real analysis" , Macmillan (1969). MR0151555 Zbl 0197.03501
[Vi]	A. Vitali, "Sulle funzioni integrali", Atti Accad. Sci. Torino Cl. Sci. Fis. Mat. Natur., 40 1905 pp. 1021-1034.