Bergman spaces
$L _ { a } ^ { p } ( G )$, $0 < p < \infty$
Spaces of analytic functions $f$ on an open set $G$ in the complex plane for which
\begin{equation*} \| f \| _ { p , G } ^ { p } = \int_G | f ( z ) | ^ { p } d A ( z ) < \infty , \end{equation*}
where $d A ( z ) = d x d y$ is the $2$-dimensional Lebesgue measure on $G$.
If $p = 2$, then $L _ { a } ^ { 2 } ( G )$ is a Hilbert space and has a reproducing kernel $k _ { z } ( w )$ satisfying $f ( z ) = \int _ { G } f ( w ) \overline { k _ { z } ( w ) } d A ( w )$ for all $f$ in $L _ { a } ^ { 2 } ( G )$ and $z$ in $G$ (cf. also Bergman kernel function). The strong connections between reproducing kernels, conformal mappings (cf. also Conformal mapping), harmonic measure, and elliptic partial differential equations (cf. also Elliptic partial differential equation) motivated the pioneering work of S. Bergman [a7]; see also, e.g., [a6].
If $p > 0$, then $L _ { a } ^ { p } ( G )$ is a closed subspace of $L ^ { p } ( G )$; thus, for $p \geq 1$ it is a Banach space with norm $\| f \| _ { p , G}$. Furthermore, a function $f \in L ^ { p } ( G )$, $p \geq 1$, has an almost-everywhere representative in $L _ { a } ^ { p } ( G )$ if and only if
\begin{equation} \tag{a1} \int _ { G } f \overline { \partial } \varphi d A = 0 \end{equation}
for all compactly supported functions $\varphi$ in $C _ { c } ^ { \infty } ( G )$. It is a result of V. Havin that via the Bergman–Sobolev duality (a1) the annihilator of $L _ { a } ^ { p } ( G )$, $p > 1$, can be identified with the Sobolev space $W _ { 0 } ^ { q , 1 } ( G )$, $1 / p + 1 / q = 1$, [a11]. If $1 < p < 2$, then the space $L _ { a } ^ { p } ( G )$ is non-trivial if and only if $\mathbf{C} \backslash G$ contains at least two points. $L _ { a } ^ { 2 } ( G )$ is non-trivial if and only if $\mathbf{C} \backslash G$ has positive logarithmic capacity, and more generally, for $p > 2$, $L _ { a } ^ { p } ( G )$ is non-trivial if and only if $\mathbf{C} \backslash G$ has positive $q$-capacity, $1 / p + 1 / q = 1$, [a8], [a12].
If $G$ is bounded, then the Cauchy transform (cf. also Cauchy integral) provides many examples of functions in a Bergman space. Indeed, if $\mu$ is a finite complex measure with compact support in the complement of $G$ and if $p > 1$, then the Cauchy transform
\begin{equation*} C _ { \mu } ( z ) = \int \frac { 1 } { z - w } d \mu ( w ) \end{equation*}
is in $L _ { a } ^ { p } ( G )$ if and only if $\mu$ has finite $q$-energy, $1 / p + 1 / q = 1$, cf. also Energy of measures. In fact, such Cauchy transforms are dense in $L _ { a } ^ { p } ( G )$ ($G$ bounded), [a12].
When $G$ equals the unit disc $D = \{ z \in \mathbf{C} : | z | < 1 \}$, then one writes $L _ { a } ^ { p } ( G ) = L _ { a } ^ { p }$ or $A ^ { p }$. For each $p > 1$ one can identify the dual 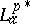 with $L _ { a } ^ { q }$, $1 / p + 1 / q = 1$, with the duality $\langle f , g \rangle = \int _ { D } f \overline{g} d A$ with equivalence of norms. One also has $B _ { 0 } ^ { * } \cong L _ { a } ^ { 1 }$ and $L _ { a } ^ { 1 * } \cong B$, where $B$ and $B_0$ are the Bloch and the little Bloch spaces (cf. also Bloch function). Furthermore, harmonic conjugation defines a bounded linear transformation on $L ^ { p }$ for all $p \geq 1$, i.e. for each $p \geq 1$ there is a $c > 0$ such that $\| \tilde { u } \| _ { p } \leq c \| u \| _ { p }$ for every harmonic function $u$ on $D$; here, $\tilde{u}$ is the harmonic conjugate of $u$, ([a3]).
with $L _ { a } ^ { q }$, $1 / p + 1 / q = 1$, with the duality $\langle f , g \rangle = \int _ { D } f \overline{g} d A$ with equivalence of norms. One also has $B _ { 0 } ^ { * } \cong L _ { a } ^ { 1 }$ and $L _ { a } ^ { 1 * } \cong B$, where $B$ and $B_0$ are the Bloch and the little Bloch spaces (cf. also Bloch function). Furthermore, harmonic conjugation defines a bounded linear transformation on $L ^ { p }$ for all $p \geq 1$, i.e. for each $p \geq 1$ there is a $c > 0$ such that $\| \tilde { u } \| _ { p } \leq c \| u \| _ { p }$ for every harmonic function $u$ on $D$; here, $\tilde{u}$ is the harmonic conjugate of $u$, ([a3]).
For the topological algebra $A ^ { - \infty } = \cup _ { p > 0 } L _ { a } ^ { p }$, B. Korenblum has established a theory that parallels the theory of Hardy spaces with regard to Riesz factorization and invariant subspaces (see [a15] [a16]).
For a fixed $p > 0$ one notes that the Hardy space $H ^ { p }$ is contained in 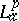 , and it is useful to contrast the function theory in
, and it is useful to contrast the function theory in 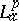 (as known today (1998)) with the classical situation in $H ^ { p }$. A general statement one can make is that results for functions in a Bergman space depend on the parameter $p > 0$.
(as known today (1998)) with the classical situation in $H ^ { p }$. A general statement one can make is that results for functions in a Bergman space depend on the parameter $p > 0$.
While a precise characterization of the 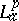 -zero sets is open (1998), certain asymptotic results are known, [a20], [a21]. Every function $f$ in
-zero sets is open (1998), certain asymptotic results are known, [a20], [a21]. Every function $f$ in 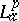 admits an "Lap-inner-Lap-outer" factorization $f = \varphi F$, [a1]. A function $\varphi$ in
admits an "Lap-inner-Lap-outer" factorization $f = \varphi F$, [a1]. A function $\varphi$ in 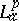 , $\| \varphi \| _ { p } = 1$, is called
, $\| \varphi \| _ { p } = 1$, is called 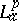 -inner if
-inner if
\begin{equation*} \int _ { D } z ^ { n } | \varphi ( z ) | ^ { p } d A ( z ) = 0 \end{equation*}
for all $n > 0$, and a function $F$ in  is called
is called 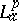 -outer if whenever $g$ is in
-outer if whenever $g$ is in 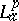 with $\|hF\|_p \geq \|hg\|_p$ for all analytic polynomials $h$, then $|F(0)|\geq |h(0)|$ (see [a17]).
with $\|hF\|_p \geq \|hg\|_p$ for all analytic polynomials $h$, then $|F(0)|\geq |h(0)|$ (see [a17]). 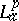 -outer functions are cyclic in
-outer functions are cyclic in 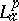 , yet, no explicit function-theoretic descriptions for either the inner or outer functions are known (1998). The inner factors are sometimes called the contractive divisors, because $\| f / \varphi \| _ { p } \leq \| f \| _ { p }$, whenever $f$ is in the invariant subspace generated by the
, yet, no explicit function-theoretic descriptions for either the inner or outer functions are known (1998). The inner factors are sometimes called the contractive divisors, because $\| f / \varphi \| _ { p } \leq \| f \| _ { p }$, whenever $f$ is in the invariant subspace generated by the 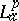 -inner function $\varphi$, [a10], [a13]. General invariant subspaces of
-inner function $\varphi$, [a10], [a13]. General invariant subspaces of 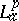 do not have to be cyclic (i.e. generated by one function) (see [a2], [a14]), but for $p = 2$ one knows that they are generated by a collection of inner functions, [a1].
do not have to be cyclic (i.e. generated by one function) (see [a2], [a14]), but for $p = 2$ one knows that they are generated by a collection of inner functions, [a1].
Interpolating sequences and sampling sequences for 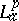 have been characterized by K. Seip [a19].
have been characterized by K. Seip [a19].
There also are well-developed theories of Toeplitz, Hankel, and composition operators on Bergman spaces, and work on Bergman spaces on domains in $\mathbf{C} ^ { n }$ has started (see e.g. [a22], [a9], [a18], [a4], [a5]).
References
| [a1] | A. Aleman, S. Richter, C. Sundberg, "Beurling's theorem for the Bergman space" Acta Math. , 177 (1996) pp. 275–310 |
| [a2] | C. Apostol, H. Bercovici, C. Foias, C. Pearcy, "Invariant subspaces, dilation theory, and the structure of the predual of a dual algebra" J. Funct. Anal. , 63 (1985) pp. 369–404 |
| [a3] | S. Axler, "Bergman spaces and their operators" J.B. Conway (ed.) B.B. Morrel (ed.) , Surveys of Some Recent Results in Operator Theory I , Res. Notes Math. , 171 , Pitman (1988) pp. 1–50 |
| [a4] | S. Axler, D. Zheng, "Compact operators via the Berezin transform" Indiana J. Math. , 49 (1998) pp. 311 |
| [a5] | "Holomorphic Spaces" S. Axler (ed.) J. McCarthy (ed.) D. Sarason (ed.) , Cambridge Univ. Press (1998) |
| [a6] | S. Bell, "The Cauchy transform, potential theory, and conformal mapping" , Studies Adv. Math. , CRC (1992) |
| [a7] | S. Bergman, "The kernel function and conformal mapping" , Math. Surveys , 5 , Amer. Math. Soc. (1950) |
| [a8] | L. Carleson, "Selected problems on exceptional sets" , v. Nostrand (1967) |
| [a9] | C. Cowen, B. MacCluer, "Composition operators on spaces of analytic functions" , Studies Adv. Math. , CRC (1995) |
| [a10] | P. Duren, D. Khavinson, H. Shapiro, C. Sundberg, "Invariant subspaces in Bergman spaces and the biharmonic equation" Michigan Math. J. , 41 (1994) pp. 247–259 |
| [a11] | V.P. Havin, "Approximation in the mean by analytic functions" Soviet Math. Dokl. , 9 (1968) pp. 245–248 |
| [a12] | L. Hedberg, "Non linear potentials and approximation in the mean by analytic functions" Math. Z. , 129 (1972) pp. 299–319 |
| [a13] | H. Hedenmalm, "A factorization theorem for square area integrable functions" J. Reine Angew. Math. , 422 (1991) pp. 45–68 |
| [a14] | H. Hedenmalm, "An invariant subspace of the Bergman space having the codimension two property" J. Reine Angew. Math. , 443 (1993) pp. 1–9 |
| [a15] | B. Korenblum, "An extension of the Nevanlinna theory" Acta Math. , 135 (1975) pp. 187–219 |
| [a16] | B. Korenblum, "A Beurling type theorem" Acta Math. , 138 (1977) pp. 265–293 |
| [a17] | B. Korenblum, "Outer functions and cyclic elements in Bergman spaces" J. Funct. Anal. , 115 (1993) pp. 104–118 |
| [a18] | H. Li, D. Luecking, "BMO on strongly pseudoconvex domains: Hankel operators, duality and $\partial$-estimates" Trans. Amer. Math. Soc. , 346 (1994) pp. 661–691 |
| [a19] | K. Seip, "Beurling type density theorems in the unit disc" Invent. Math. , 113 (1993) pp. 21–39 |
| [a20] | K. Seip, "On a theorem of Korenblum" Ark. Mat. , 32 (1994) pp. 237–243 |
| [a21] | K. Seip, "On Korenblum's density condition for the zero sets of $A _ { p , \alpha }$" J. Anal. Math. , 67 (1995) pp. 307–322 |
| [a22] | K. Zhu, "Operator theory in function spaces" Pure Appl. Math. , 139 (1990) |
Bergman spaces. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bergman_spaces&oldid=55344