Base change
change of base
A category-theoretical construction; special cases are the concept of an induced fibration in topology, and extension of the ring of scalars in the theory of modules.
Let 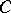 be a category with fibred products and let
be a category with fibred products and let 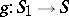 be a morphism of
be a morphism of  . A base change by means of
. A base change by means of 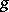 is a functor from the category of
is a functor from the category of 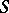 -objects (i.e. the category of morphism
-objects (i.e. the category of morphism 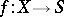 , where
, where 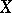 is an object of
is an object of 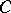 ) to the category of
) to the category of 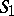 -objects, taking an
-objects, taking an 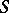 -object
-object 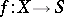 to the
to the 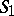 -object
-object 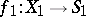 , where
, where  and
and 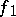 is projection onto the second factor. The morphism
is projection onto the second factor. The morphism 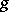 is then called the base-change morphism. One also says that
is then called the base-change morphism. One also says that 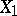 is obtained from
is obtained from 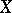 by base change.
by base change.
A special case of a base change is the concept of a fibre of a morphism 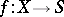 of schemes
of schemes  : The fibre of the morphism
: The fibre of the morphism 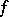 over a point
over a point  is the scheme
is the scheme
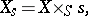 |
i.e. the scheme obtained from 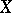 by base change via the natural morphism
by base change via the natural morphism 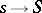 . A similar definition yields the geometric fibre
. A similar definition yields the geometric fibre 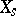 ; it is obtained by base change via the morphism
; it is obtained by base change via the morphism 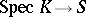 associated with a geometric point of
associated with a geometric point of 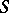 , where
, where 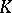 is an algebraically closed field. Many properties of the
is an algebraically closed field. Many properties of the 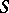 -scheme
-scheme 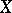 are preserved under a base change. The inverse problem — to infer the properties of a scheme
are preserved under a base change. The inverse problem — to infer the properties of a scheme 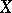 from those of the schemes obtained from
from those of the schemes obtained from 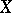 by base change — is considered in descent theory (see also [3]).
by base change — is considered in descent theory (see also [3]).
Let 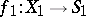 be the morphism obtained from
be the morphism obtained from 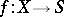 via a morphism
via a morphism 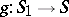 , so that one has a Cartesian square
, so that one has a Cartesian square
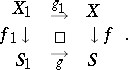 |
Let 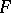 be a sheaf of sets on
be a sheaf of sets on 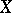 . Then there exists a natural sheaf mapping
. Then there exists a natural sheaf mapping 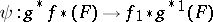 . If
. If 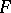 is a sheaf of Abelian groups, then for every
is a sheaf of Abelian groups, then for every 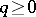 there exists a natural sheaf homomorphism
there exists a natural sheaf homomorphism
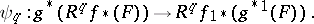 |
Under these conditions, 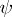 and
and 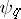 are also called base-change morphisms. It is usually said that the base-change theorem is valid if
are also called base-change morphisms. It is usually said that the base-change theorem is valid if 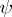 (or
(or 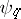 ) is an isomorphism. In other words, the base-change theorem is a proposition about the compatibility (commutability) of the functors
) is an isomorphism. In other words, the base-change theorem is a proposition about the compatibility (commutability) of the functors 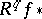 with the base-change functor. In particular, if
with the base-change functor. In particular, if 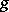 is the imbedding of a point
is the imbedding of a point 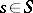 , the base-change theorem states that there exists a natural isomorphism
, the base-change theorem states that there exists a natural isomorphism 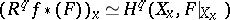 between the fibre of the
between the fibre of the 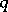 -th direct image of the sheaf
-th direct image of the sheaf 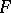 and the
and the 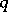 -dimensional cohomology group of the fibre of the morphism
-dimensional cohomology group of the fibre of the morphism 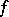 . The base-change theorem is valid in the following situations: 1)
. The base-change theorem is valid in the following situations: 1) 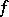 is a proper mapping of paracompact topological spaces,
is a proper mapping of paracompact topological spaces,  is a locally compact space [1]; 2)
is a locally compact space [1]; 2)  is a separable quasi-compact morphism of schemes,
is a separable quasi-compact morphism of schemes, 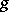 is a flat morphism,
is a flat morphism, 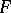 is a quasi-coherent sheaf of
is a quasi-coherent sheaf of 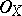 -modules (the comparison theorem for the cohomology of ordinary and formal schemes — see [2] — can also be interpreted as a base-change theorem); or 3)
-modules (the comparison theorem for the cohomology of ordinary and formal schemes — see [2] — can also be interpreted as a base-change theorem); or 3) 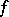 is a proper morphism of schemes,
is a proper morphism of schemes, 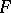 is a torsion sheaf in the étale topology. Some other cases in which base-change theorems are valid are considered in [3].
is a torsion sheaf in the étale topology. Some other cases in which base-change theorems are valid are considered in [3].
References
| [1] | R. Godement, "Topologie algébrique et théorie des faisceaux" , Hermann (1958) |
| [2] | A. Grothendieck, J. Dieudonné, "Eléments de géometrie algébrique" Publ. Math. IHES , 11 (1961) |
| [3] | "Théorie des topos et cohomologie étale des schémas" M. Artin (ed.) A. Grothendieck (ed.) J.-L. Verdier (ed.) , Sem. Geom. Alg. , 4 , Springer (1973) |
Base change. V.I. Danilov (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Base_change&oldid=14478