A well-known and widely-used process for determining the roots of a given polynomial with real coefficients. The method determines a second-degree divisor of the given polynomial iteratively, and hence by using the formula for the roots of second-degree polynomials one can calculate an approximation of two roots of the given polynomial. An advantage of the method is that it uses real arithmetic only.
Let
be a given polynomial with real coefficients and  . After division by
. After division by  one finds
one finds
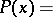 | (a1) |
where  and
and  are the coefficients of the remainder. It is now necessary to find two real numbers,
are the coefficients of the remainder. It is now necessary to find two real numbers,  and
and  , so that
, so that  is a divisor of
is a divisor of 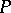 . This is equivalent to the solution of a system of non-linear equations
. This is equivalent to the solution of a system of non-linear equations
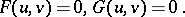 | (a2) |
Bairstow's method is nothing else than a Newton method applied to (a2). More precisely,
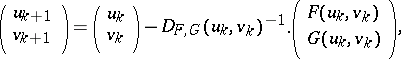 | (a3) |
where
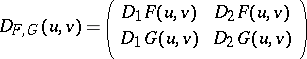 | (a4) |
is the Jacobian matrix (cf. Jacobi matrix) and 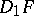 ,
, 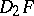 ,
, 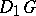 , and
, and 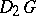 denote the partial derivatives of
denote the partial derivatives of 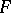 and
and  with respect to the first and second argument, respectively. If
with respect to the first and second argument, respectively. If  is not invertible, then the method is undefined.
is not invertible, then the method is undefined.
It is important that 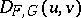 is determined by the remainders of
is determined by the remainders of  and
and  after division by
after division by 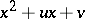 . Express the polynomial
. Express the polynomial  as
as
Then the Jacobian matrix (a4) has the following elements:
For the proof see [a1].
The values  ,
,  and
and 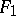 ,
,  can be found by means of a Horner-type scheme (cf. Horner scheme). Using
can be found by means of a Horner-type scheme (cf. Horner scheme). Using
and
one finds the same recursion for 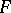 ,
, 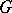 ,
, 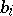 and
and 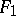 ,
,  ,
,  :
:
The main assumption in local convergence theorems for the Newton method is the non-singularity of the Jacobian matrix at the root. The following theorem gives a necessary and sufficient condition of algebraic character for this to hold.
Let  and
and  be arbitrary real numbers. The Jacobian matrix
be arbitrary real numbers. The Jacobian matrix 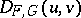 introduced in (a4) is regular if and only if
introduced in (a4) is regular if and only if  and the polynomial
and the polynomial 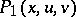 defined by (a1) have no common root. The rank of
defined by (a1) have no common root. The rank of 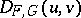 is one if and only if the number of the common roots is one. The Jacobian matrix is zero if and only if
is one if and only if the number of the common roots is one. The Jacobian matrix is zero if and only if 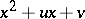 is a divisor of
is a divisor of 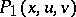 . For the proof see [a2].
. For the proof see [a2].
Using the local convergence theorem for the Newton method one obtains, as a corollary, the local convergence theorem for the Bairstow method:
Let
and suppose that the two factors on the right-hand side have no common root. Then there exists a positive number 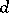 such that the sequence
such that the sequence 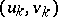 produced by Bairstow's method will converge (quadratically) to
produced by Bairstow's method will converge (quadratically) to 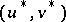 , provided
, provided
References
| [a1] | J. Stoer, R. Bulirsch, "Introduction to numerical analysis" , Springer (1980) pp. 285–287 |
| [a2] | T. Fiala, A. Krebsz, "On the convergence and divergence of Bairstow's method" Numerische Math. , 50 (1987) pp. 477–482 |
How to Cite This Entry:
Bairstow method. A. Krebsz (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bairstow_method&oldid=14717
This text originally appeared in Encyclopedia of Mathematics - ISBN 1402006098

 . After division by
. After division by  one finds
one finds
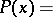
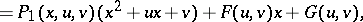
 and
and  are the coefficients of the remainder. It is now necessary to find two real numbers,
are the coefficients of the remainder. It is now necessary to find two real numbers,  and
and  , so that
, so that  is a divisor of
is a divisor of 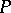 . This is equivalent to the solution of a system of non-linear equations
. This is equivalent to the solution of a system of non-linear equations
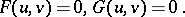
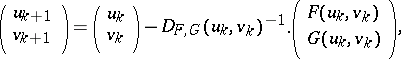
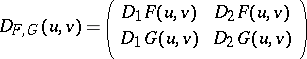
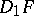 ,
, 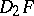 ,
, 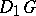 , and
, and 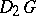 denote the partial derivatives of
denote the partial derivatives of 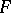 and
and  with respect to the first and second argument, respectively. If
with respect to the first and second argument, respectively. If  is not invertible, then the method is undefined.
is not invertible, then the method is undefined.
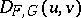 is determined by the remainders of
is determined by the remainders of  and
and  after division by
after division by 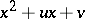 . Express the polynomial
. Express the polynomial  as
as
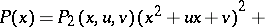
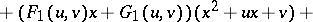
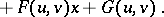
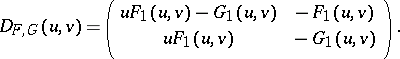
 ,
,  and
and 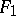 ,
,  can be found by means of a Horner-type scheme (cf. Horner scheme). Using
can be found by means of a Horner-type scheme (cf. Horner scheme). Using
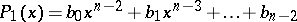
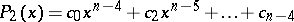
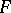 ,
, 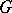 ,
, 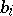 and
and 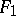 ,
,  ,
,  :
:
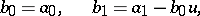
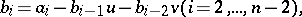

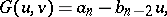
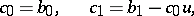
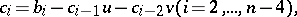
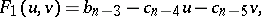
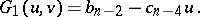
 and
and  be arbitrary real numbers. The Jacobian matrix
be arbitrary real numbers. The Jacobian matrix 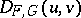 introduced in (a4) is regular if and only if
introduced in (a4) is regular if and only if  and the polynomial
and the polynomial 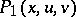 defined by (a1) have no common root. The rank of
defined by (a1) have no common root. The rank of 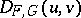 is one if and only if the number of the common roots is one. The Jacobian matrix is zero if and only if
is one if and only if the number of the common roots is one. The Jacobian matrix is zero if and only if 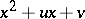 is a divisor of
is a divisor of 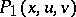 . For the proof see [a2].
. For the proof see [a2].
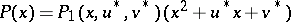
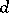 such that the sequence
such that the sequence 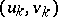 produced by Bairstow's method will converge (quadratically) to
produced by Bairstow's method will converge (quadratically) to 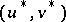 , provided
, provided
